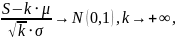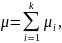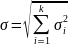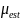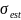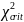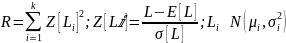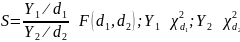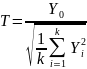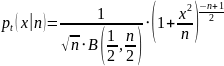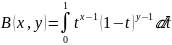ПР4

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА  Российский технологический университет» РТУ МИРЭА

Институт информационных технологий (ИИТ)

Кафедра прикладной математики (ПМ)

ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ

по дисциплине «Прикладные задачи математической статистики»

Практическое занятие № 4

Студент группы ИНБО-01-17	ИНБО-06-20	(подпись)
Преподаватель	Юрченков И.А.	(подпись)
Отчет представлен	«17» декабря 2022 г.

Москва 2022 г.

Постановка задачи

1. Сгенерировать выборку нормального распределения 𝑌 ∼ 𝑁 (𝜇, 𝜎2) используя определение центральной предельной теоремы.

2. Сгенерировать выборку 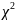-распределения R ~ 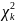используя определение распределения -распределения.

3. Сгенерировать выборку распределения Фишера на основе определения.

4. Сгенерировать выборку t-распределения на основе определения.

Ход выполнения работы

1. Составим выборку, подчиняющуюся нормальному распределению, воспользовавшись определением центральной предельной теоремы (ЦПТ).

В одной из формулировок ЦПТ звучит следующим образом: случайная величина, составленная в виде суммы 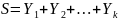случайных величин 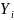с неодинаковыми математическим ожиданием 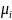и стандартным отклонением 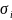, обладает следующим свойством (1):

(1)

где 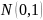— стандартное нормальное распределение.

При этом математическое ожидание 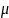полученной случайной величины 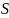рассчитывается по формуле (2):

(2)

Стандартное отклонение 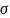полученной случайной величины рассчитывается по формуле (3):

(3)

Сгенерируем k = 15 различных равномерно распределённых выборок по n = 500 элементов.

Рассчитаем м.о. и с.о. случайной величины при помощи точечных оценок, приведённых в формулах 2-3. 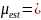29.68, 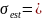3.72.

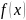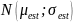Построим на одном графику гистограмму нашей случайной величины, делёную на ширину интервала, а также функцию плотности нормального распределения для рассчитанных точечных оценок параметров ( для ). Полученный график представлен на Рисунке 1.

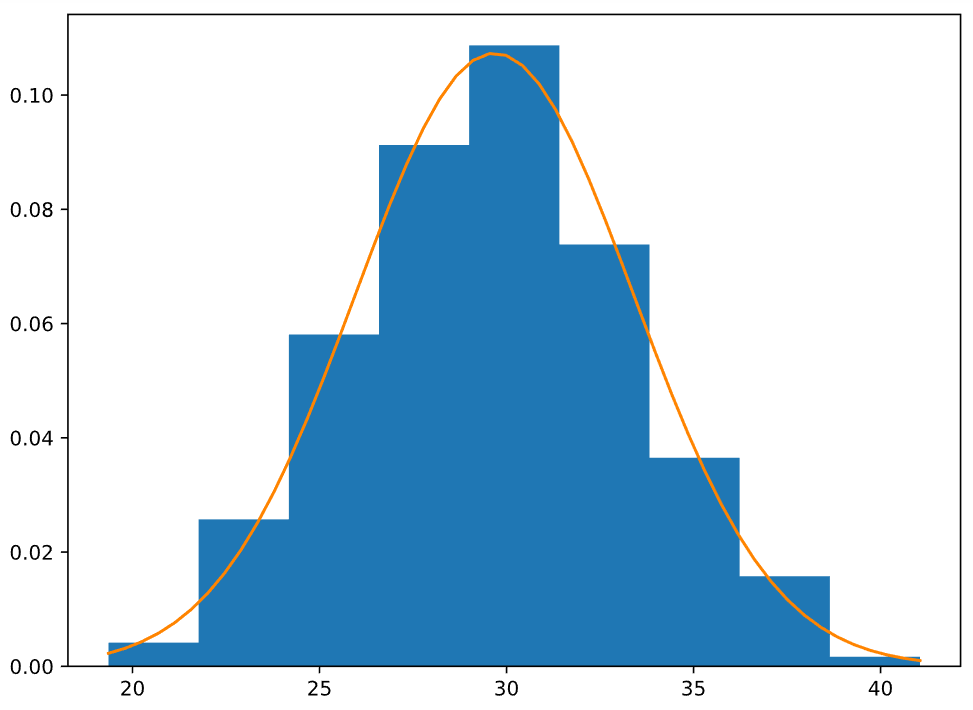
Рисунок 1 — График гистограммы полученной выборки и функции плотности нормального распределения при рассчитанных точечных оценках параметров

Проведём тест на нормальное распределение с помощью критерия 𝜒2-Пирсона.

Для этого найдём гистограмму нашей выборки и рассчитаем теоретические частоты для нормального распределения с параметрами, для которых ранее была получена точечная оценка. На Рисунке 2 приведён график гистограмм реального и теоретического распределений.

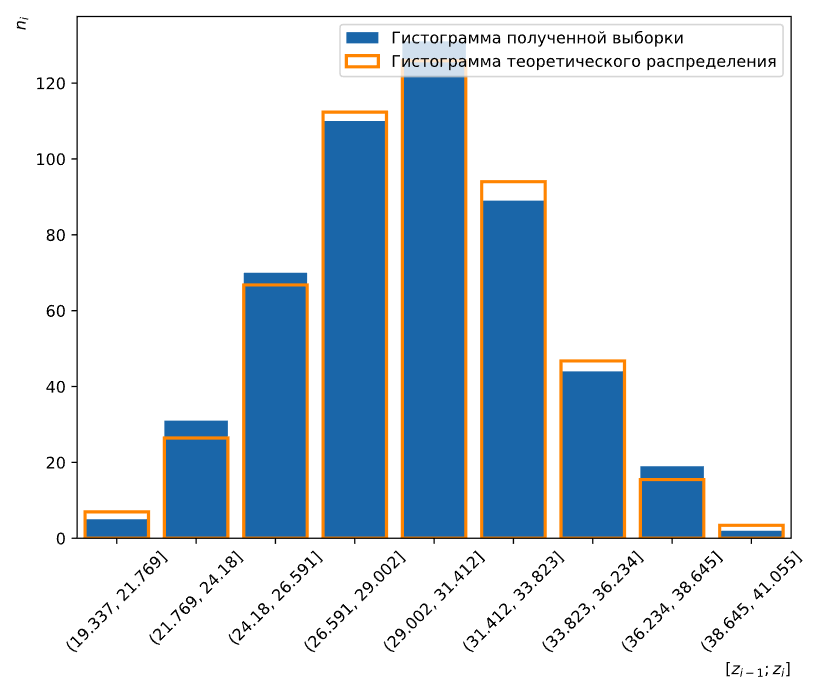
Рисунок 2 — График гистограмм выборки и теоретического распределения

Для полученных частот критерий Пирсона равен 3.56 при критическом значении 12.59. Критерий меньше критического значения, следовательно, мы принимаем нулевую гипотезу H₀ о том, что наша выборка распределена по нормальному закону с 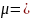29.68, 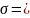3.72.

Качественно определим влияние числа сгенерированных равномерно распределенных величин на итоговое качество генерации нормального распределения при помощи взятия 3 тестовых генераций при разных n и проведения теста на распределение.

Тестовая генерация при k = 1.

Таблица 1 — Результаты расчётов для выборки, полученной при k = 1

				Вывод
10.29	0.63	123.15	12.59	Отвергается нулевая гипотеза о том, что полученная выборка распределена по нормальному закону

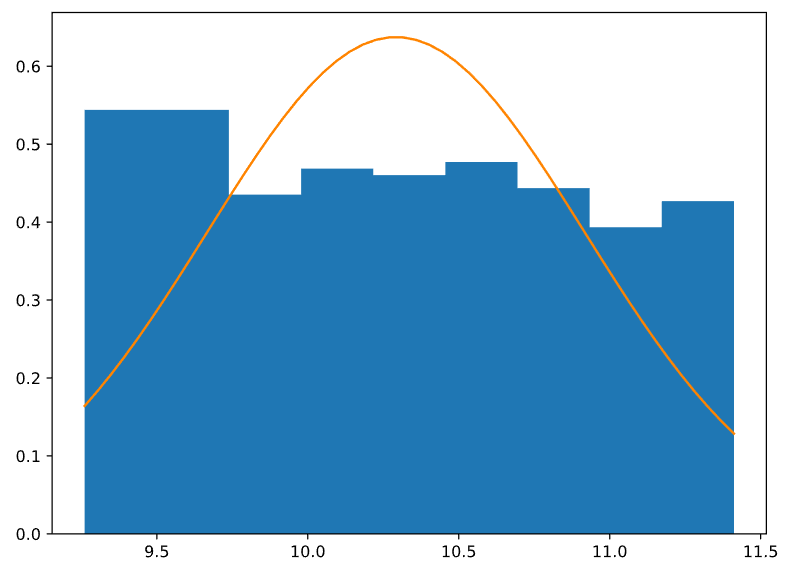
Рисунок 3 — График гистограммы выборки и функции плотности распределения для k = 1

Рисунок 4 — График гистограмм выборки и теоретического распределения для k = 1

Тестовая генерация при k = 2.

Таблица 2 — Результаты расчётов для выборки, полученной при k = 2

				Вывод
-0.59	1.71	23.73	12.59	Отвергается нулевая гипотеза о том, что полученная выборка распределена по нормальному закону

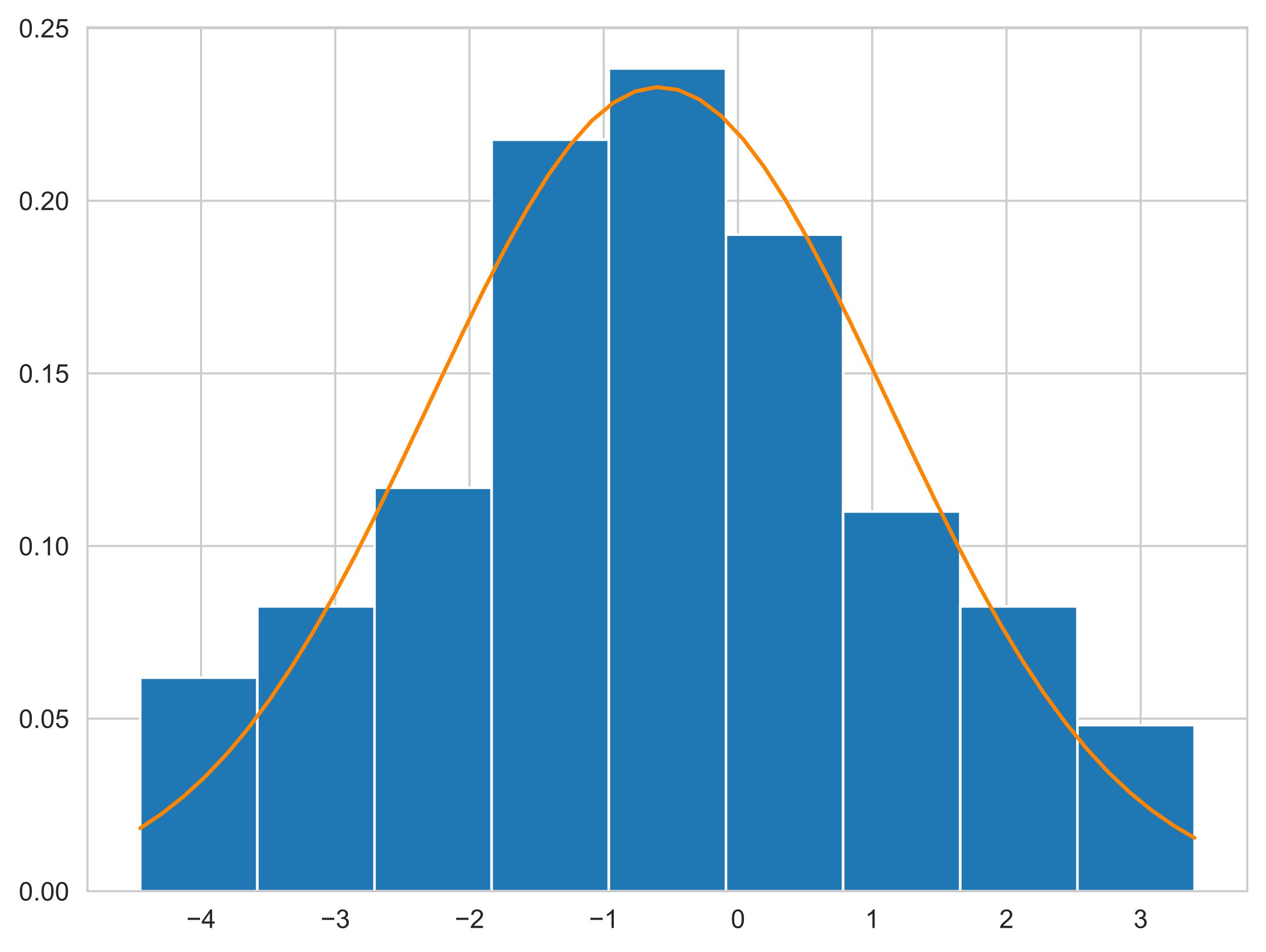
Рисунок 5 — График гистограммы выборки и функции плотности распределения для k = 2

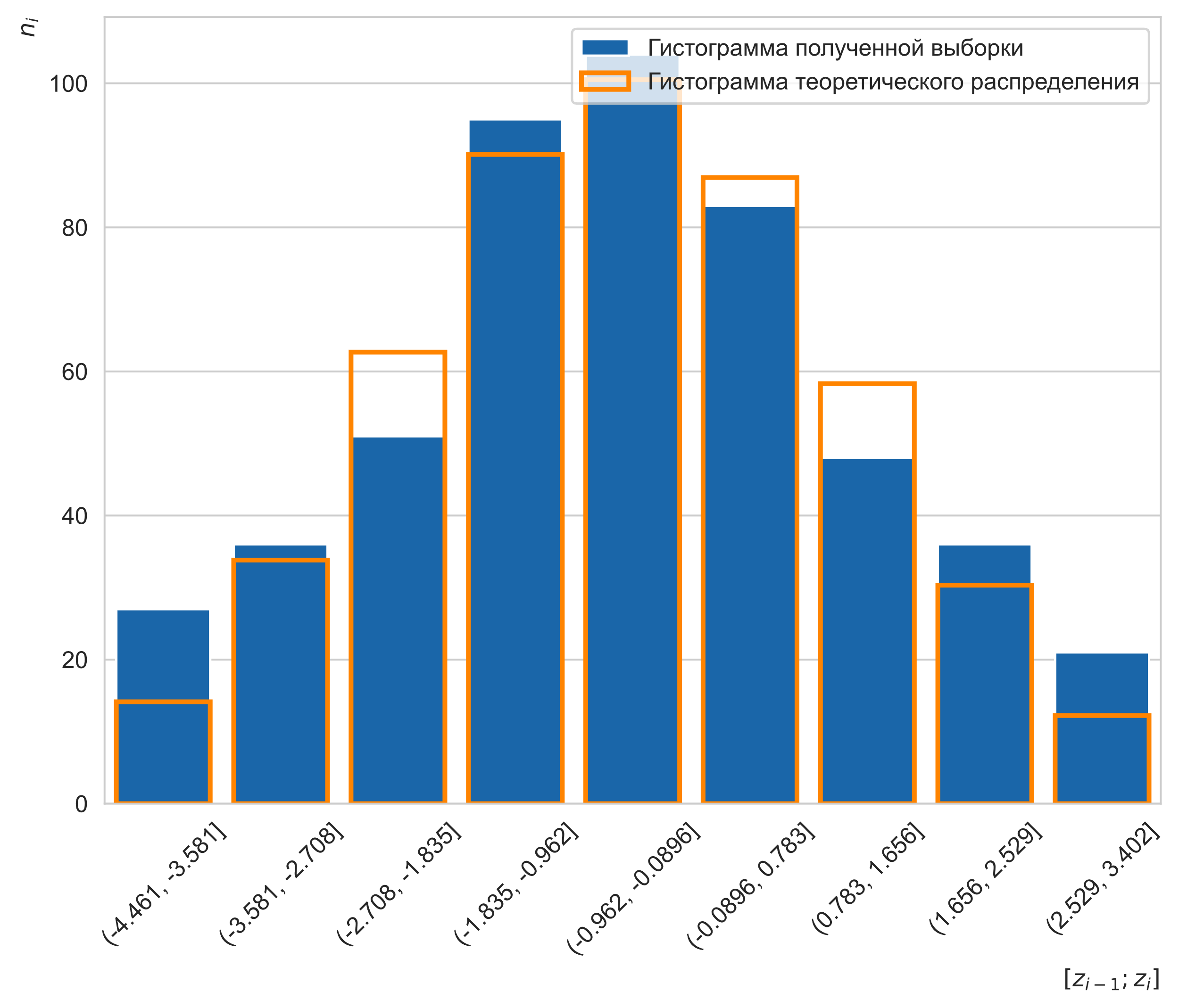
Рисунок 6 — График гистограмм выборки и теоретического распределения для k = 2

Тестовая генерация при k = 5.

Таблица 3 — Результаты расчётов для выборки, полученной при k = 5

				Вывод
24.43	2.45	8	12.59	Принимается нулевая гипотеза о том, что полученная выборка распределена по нормальному закону

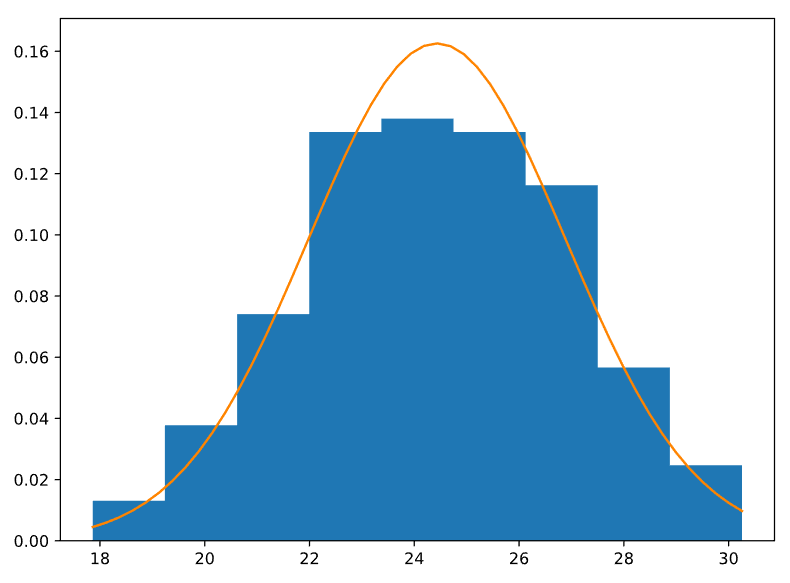
Рисунок 7 — График гистограммы выборки и функции плотности распределения для k = 5

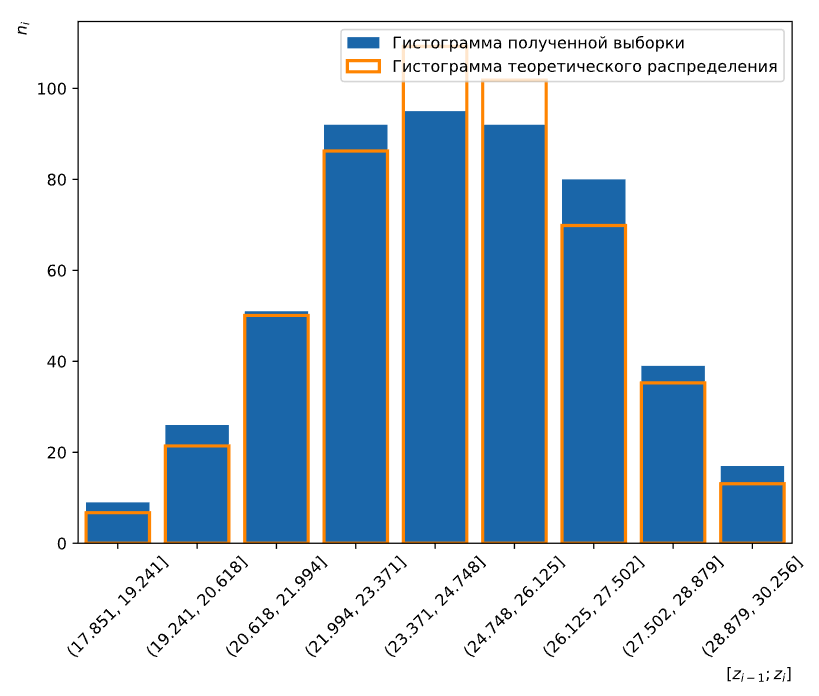
Рисунок 8 — График гистограмм выборки и теоретического распределения для k = 5

2. Составим выборку, подчиняющуюся хи-квадрат распределению, воспользовавшись определением хи-квадрат распределения.

Пусть имеется n случайных величин, распределённых по нормальному закону с различными м. о. и с. о. Тогда сумма квадратов Z-оценок этих величин R будет распределена по хи-квадрат закону (4):

(4)

Сгенерируем k = 5 различных равномерно распределённых выборок по n = 500 элементов.

Построим на одном графике гистограмму нашей случайной величины, делёную на ширину интервала, а также функцию плотности хи-квадрат распределения для степени свободы d = k. Полученный график представлен на Рисунке 9.

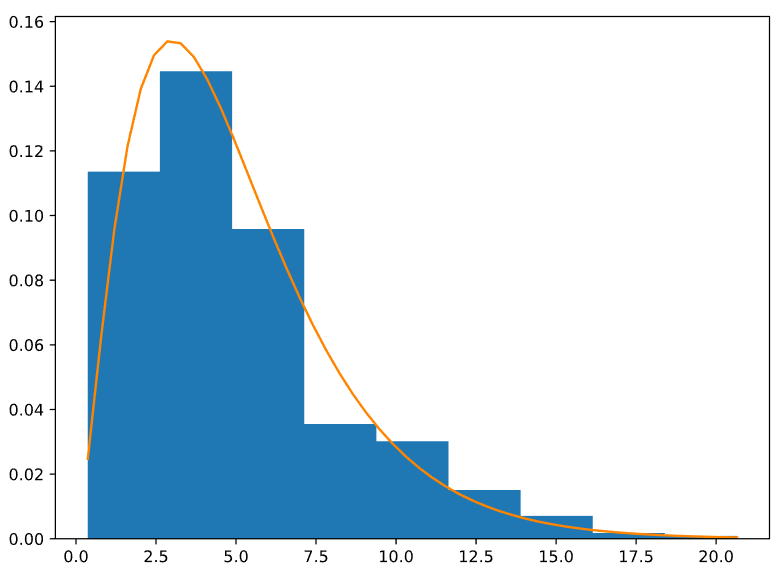
Рисунок 9 — График гистограммы полученной выборки и функции плотности хи-квадрат распределения со степенью свободы d = k = 5

Проведём тест на хи-квадрат распределение с помощью критерия 𝜒2-Пирсона.

На Рисунке 10 приведён график гистограмм реального и теоретического распределений.

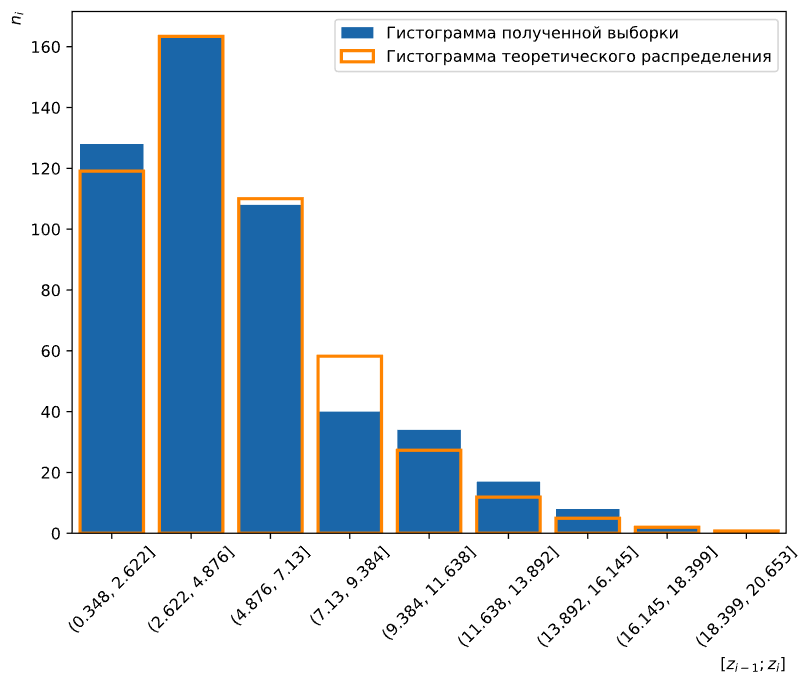
Рисунок 10 — График гистограмм выборки и теоретического распределения

Для полученных частот критерий Пирсона равен 12.22 при критическом значении 14.07. Критерий меньше критического значения, следовательно, мы принимаем нулевую гипотезу H₀ о том, что наша выборка распределена по хи-квадрат закону со степенями свободы d = k = 5.

3. Сгенерируем выборку распределения Фишера на основе определения распределения Фишера.

Пусть имеется две случайных величины, распределённых по хи-квадрат закону со степенями свободы d₁ и d₂. Тогда отношение этих случайных величин, делёных на свои степени свободы, имеет распределение Фишера со степенями свободы d₁ и d₂ (5):

(5)

Сгенерируем две выборки, распределённых по хи-квадрат закону с различными степенями d₁ и d₂, из n = 700 элементов.

Построим на одном графике гистограмму нашей случайной величины, делёную на ширину интервала, а также функцию плотности распределения Фишера со степенями свободы d₁ и d₂. Полученный график представлен на Рисунке 11.

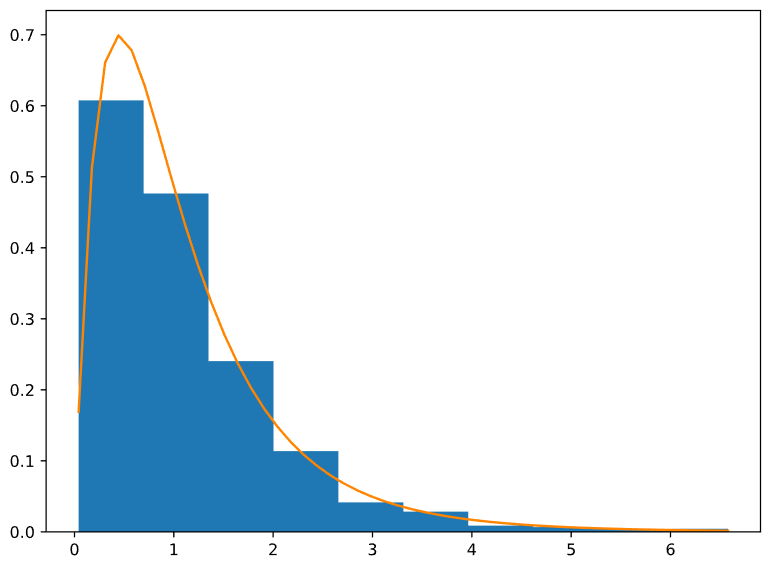
Рисунок 11 — График гистограммы полученной выборки и функции плотности распределения Фишера со степенями свободы d₁ и d₂

Проведём тест на распределение Фишера с помощью критерия 𝜒2-Пирсона.

Для этого найдём гистограмму нашей выборки и рассчитаем теоретические частоты для распределения Фишера со степенями свободы d₁ и d₂. На Рисунке 12 приведён график гистограмм реального и теоретического распределений.

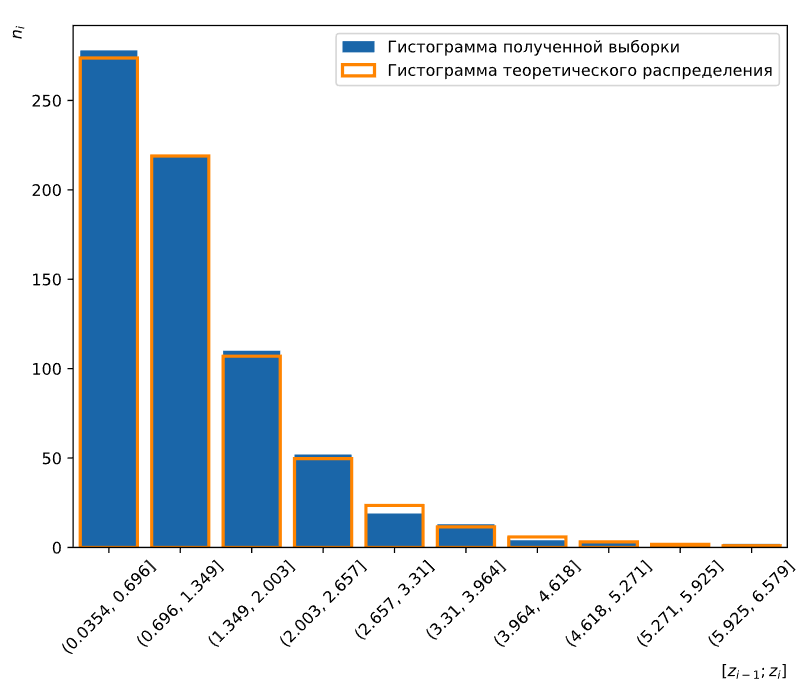
Рисунок 12 — График гистограмм выборки и теоретического распределения

Для полученных частот критерий Пирсона равен 3.06 при критическом значении 14.07. Критерий меньше критического значения, следовательно, мы принимаем нулевую гипотезу H₀ о том, что наша выборка распределена по закону Фишера со степенями свободы d₁ и d₂.

4. Составим выборку t-распределения на основе определения.

Пусть имеются k+1 случайных величин 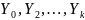, имеющих стандартное нормальное распределение. Тогда случайная величина, рассчитываемая по формуле (6), имеет распределение Стьюдента с d = k степенями свободы:

(6)

Функция плотности t-распределения имеет вид (7):

(7)

где B(x, y) — бета-функция.

Бета-функция рассчитывается по формуле (8)

(8)

Сгенерируем k = 5 стандартно распределённых выборок по n = 500 элементов.

Построим на одном графике гистограмму нашей случайной величины, делёную на ширину интервала, а также функцию плотности t-распределения с k степенями свободы. Полученный график представлен на Рисунке 13.

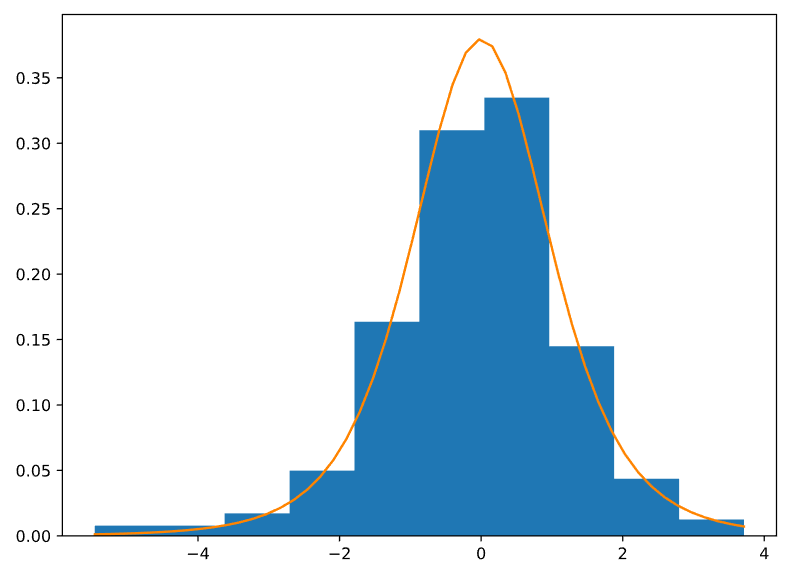
Рисунок 13 — График гистограммы полученной выборки и функции плотности t-распределения со степенью свободы k

Проведём тест на t-распределение с помощью критерия 𝜒2-Пирсона.

Для этого найдём гистограмму нашей выборки и рассчитаем теоретические частоты для t-распределения со степенью свободы k = 5. На Рисунке 14 приведён график гистограмм реального и теоретического распределений.

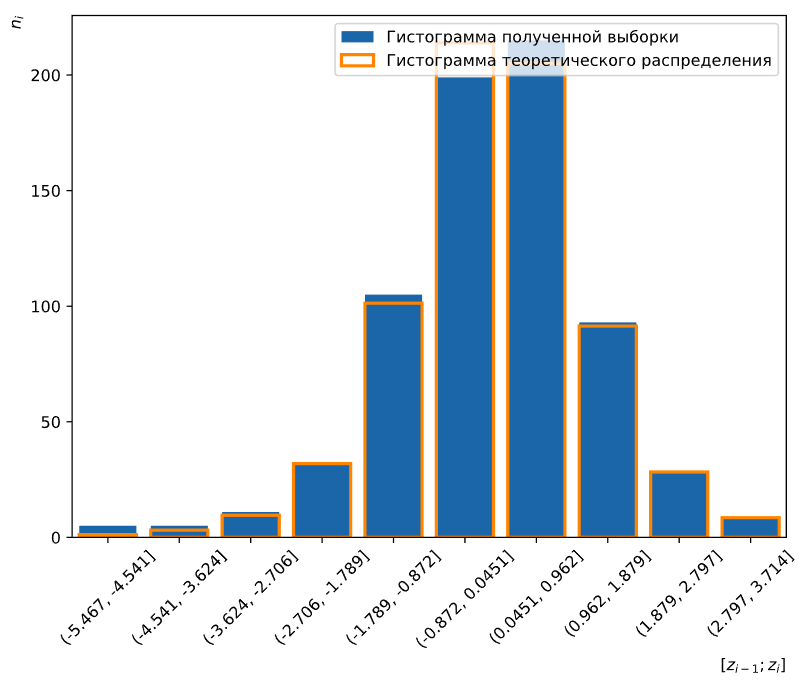
Рисунок 14 — График гистограмм выборки и теоретического распределения

Для полученных частот критерий Пирсона равен 8.05 при критическом значении 14.07. Критерий меньше критического значения, следовательно, мы принимаем нулевую гипотезу H₀ о том, что наша выборка распределена по закону Стьюдента со степенью свободы k = 5.

Вывод

В результате выполнения данной практической работы мы сгенерировали выборку нормального распределения, используя определение центральной предельной теоремы, сгенерировали выборку хи-квадрат распределения по определению, сгенерировали выборку распределения Фишера по определению, сгенерировали выборку t-распределения по определению. Для каждой из полученных выборок проверили соответствие искомому распределению при помощи критерия Пирсона.