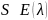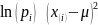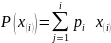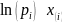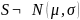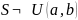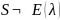ПР3
.docx
МИНОБРНАУКИ РОССИИ |
Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА Российский технологический университет» РТУ
МИРЭА
|
Институт информационных технологий (ИИТ)
Кафедра прикладной математики (ПМ)
ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ
по дисциплине «Прикладные задачи математической статистики»
Практическое задание № 3
Студент группы ИНБО-01-17
|
ИНБО-06-20 |
(подпись)
|
|
|
Преподаватель
|
Юрченков И. А.
|
(подпись)
|
|
|
Отчет представлен |
«12» декабря 2022 г. |
|
||
Москва 2022 г.
Постановка задачи:
Скачать папку с исходными данными по ссылке. Открыть папку, соответствующую своей группе. Далее открыть папку с вариантом, совпадающим с вашим номером в списке.
В папке 6 файлов с данными. Данные имеют различные распределения:
• 1 и 4 файлы - нормальное распределение;
• 2 и 5 файлы - равномерное распределение;
• 3 и 6 файлы - показательное распределение.
Необходимо идентифицировать распределения в каждом файле двумя способами:
- с помощью критерия согласия Пирсона;
-методом анаморфоз.
Методом Пирсона для каждого файла нужно проверить истинное распределение (то, к которому действительно относятся данные в файле, оно дано выше) и одно ложное. Например, если данные в файле распределены нормально, то нужно проверить нормальное распределение и одно из двух: показательное или равномерное. При расчете теоретических частот в качестве параметров распределений брать их точечные несмещенные оценки.
В отчет вставить гистограммы по каждому файлу, расчетные формулы и результаты проверки распределения.
При проверке распределения методом анаморфоз нужно построить 3 графика для каждого из 6 файлов. Каждый график представлен в координатах соответствующей анаморфозы. Тот график, на котором достигнуто спрямление, соответствует истинному распределению. Для проверки качества спрямления необходимо построить линейный тренд (провести линейную регрессию) и показать значения коэффициента детерминации (𝑅2). Он должен быть близок к 1.
По параметрам прямой (угловому коэффициенту и свободному члену) найти параметры распределения. Для построения анаморфозы нормального распределения мат. ожидание заменить его несмещенной точечной оценкой.
В выводах сравнить результаты, полученные двумя способами.
Исходные данные:
В качестве исходных данных дано шесть статистических рядов. Ряды 1-3 имеют 32 значения. Ряды 4-6 имеют 128 значений.
Ход работы:
Перед
применением тестов необходимо сформировать
гистограммы данных и расcчитать число
групп 𝑔,
границы групп
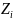 , 𝑖
∈
, 𝑖
∈
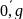 ,
абсолютные и относительные частоты
групп (
,
абсолютные и относительные частоты
групп (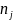 ,
,
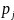 ),
𝑗
∈
),
𝑗
∈
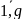 ,
опираясь на значения полученной выборки
данных. Узел «Квантование» в Loginom
рассчитывает данные параметры
автоматически, так что применение формул
не требуется.
,
опираясь на значения полученной выборки
данных. Узел «Квантование» в Loginom
рассчитывает данные параметры
автоматически, так что применение формул
не требуется.
Затем необходимо построить вариационный ряд для подсчёта абсолютных и относительных частот. Результат представлен на Рисунках 1-6.
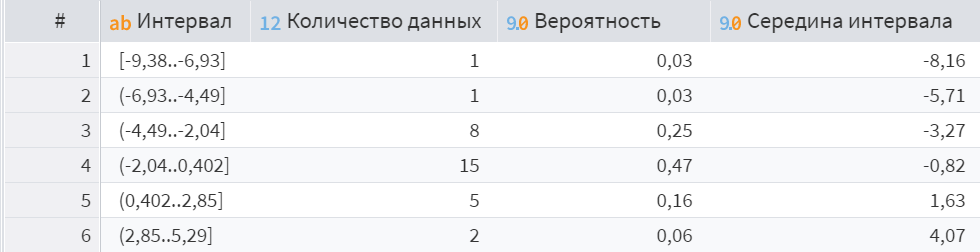
Рисунок 1 – Вариационный ряд для первого набора данных
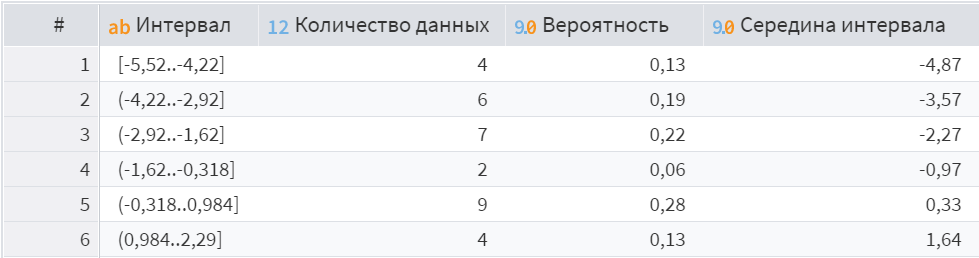
Рисунок 2 – Вариационный ряд для второго набора данных

Рисунок 3 – Вариационный ряд для третьего набора данных
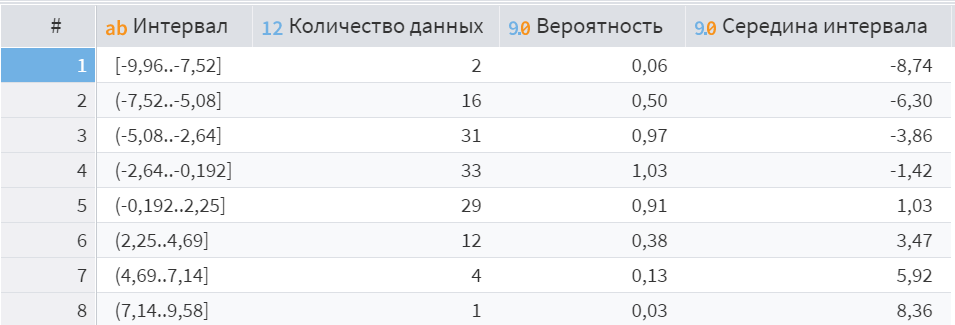
Рисунок 4 – Вариационный ряд для четвертого набора данных
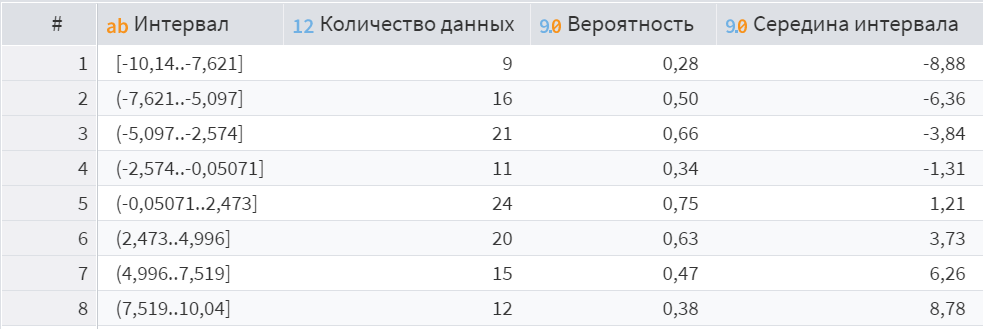
Рисунок 5 – Вариационный ряд для пятого набора данных
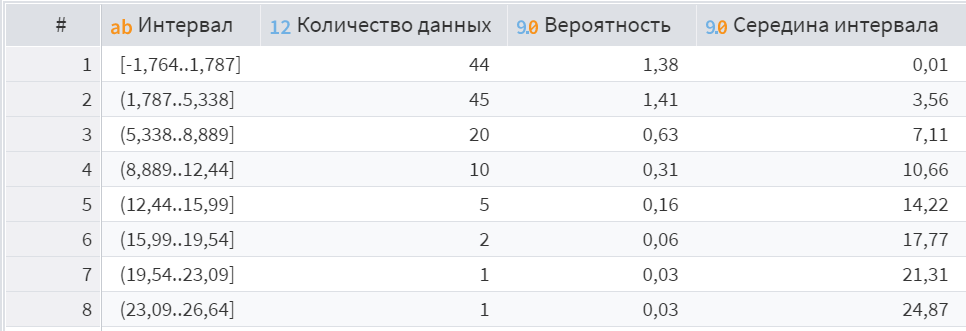
Рисунок 6 – Вариационный ряд для шестого набора данных
По результатам расчетов вариационного ряда наступает возможность визуализировать практическое приближенное распределение значений выборки в виде гистограммы. Результат представлен на Рисунках 7-12.
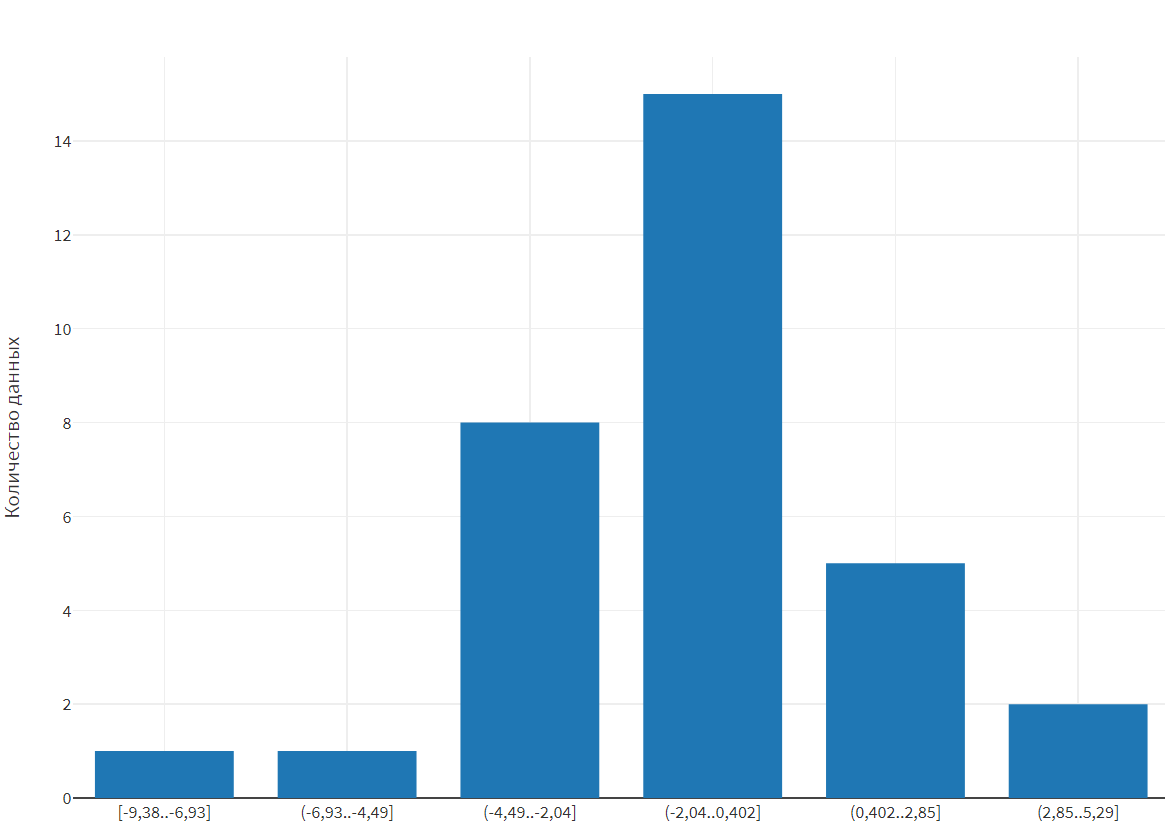
Рисунок 7 – Гистограмма для первого набора данных
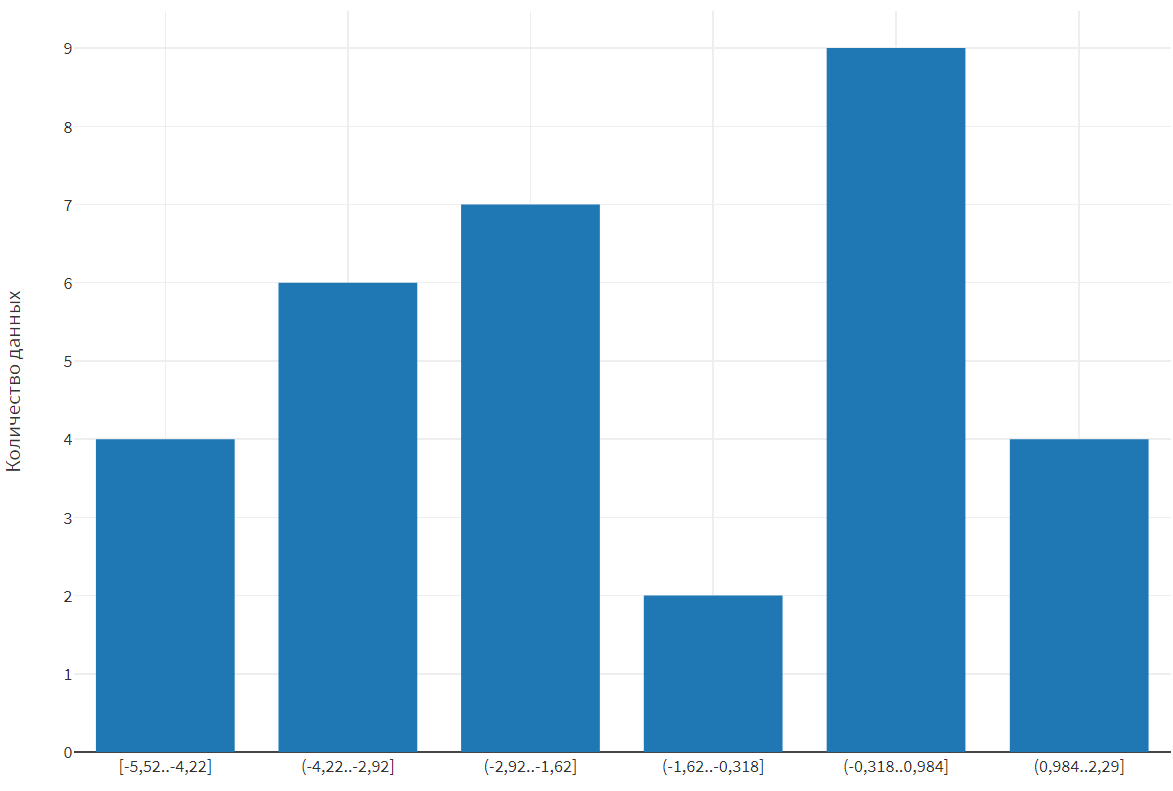
Рисунок 8 – Гистограмма для второго набора данных
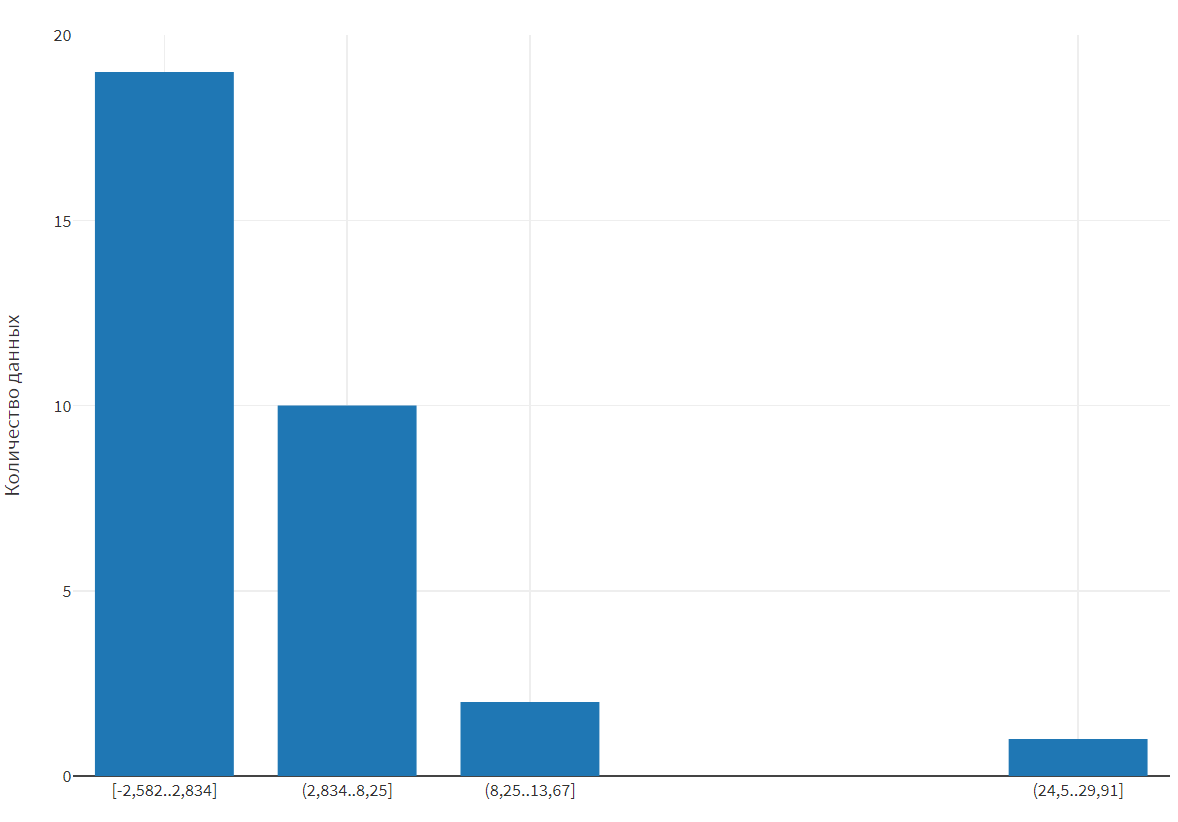
Рисунок 9 – Гистограмма для третьего набора данных
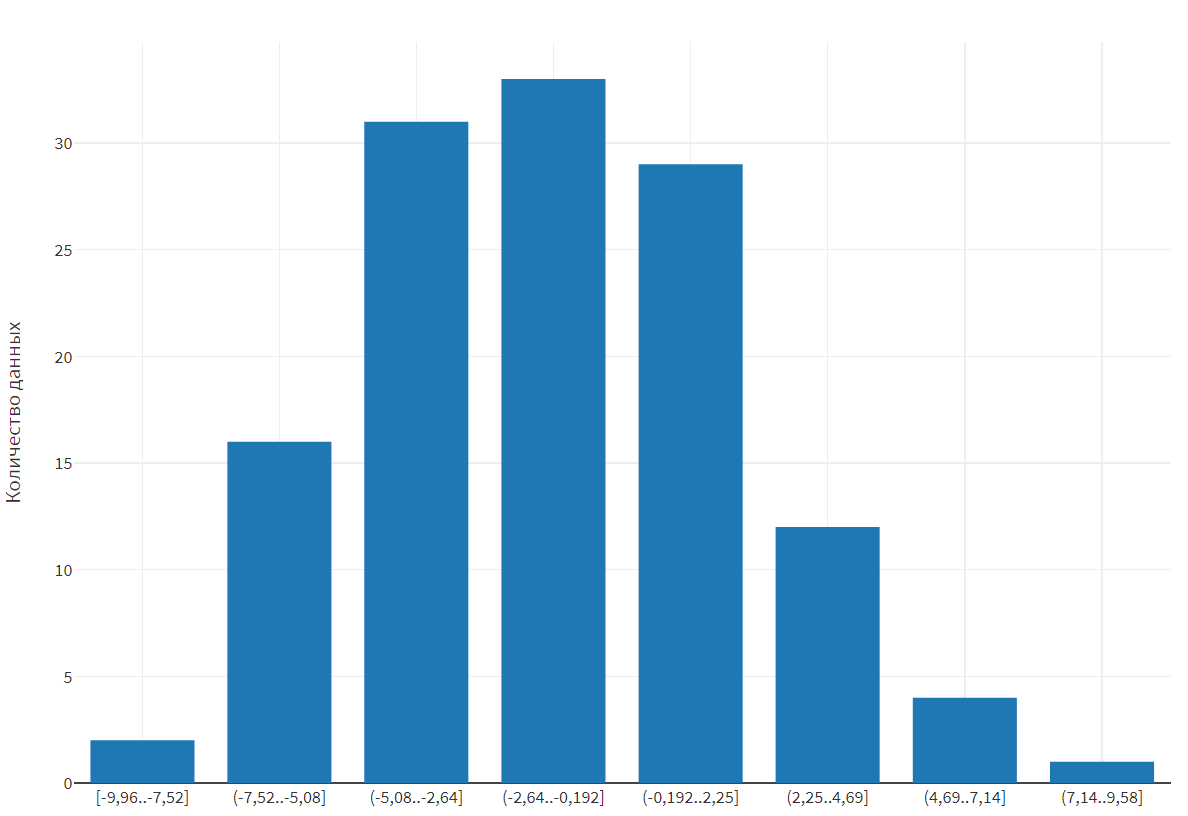
Рисунок 10 – Гистограмма для четвертого набора данных
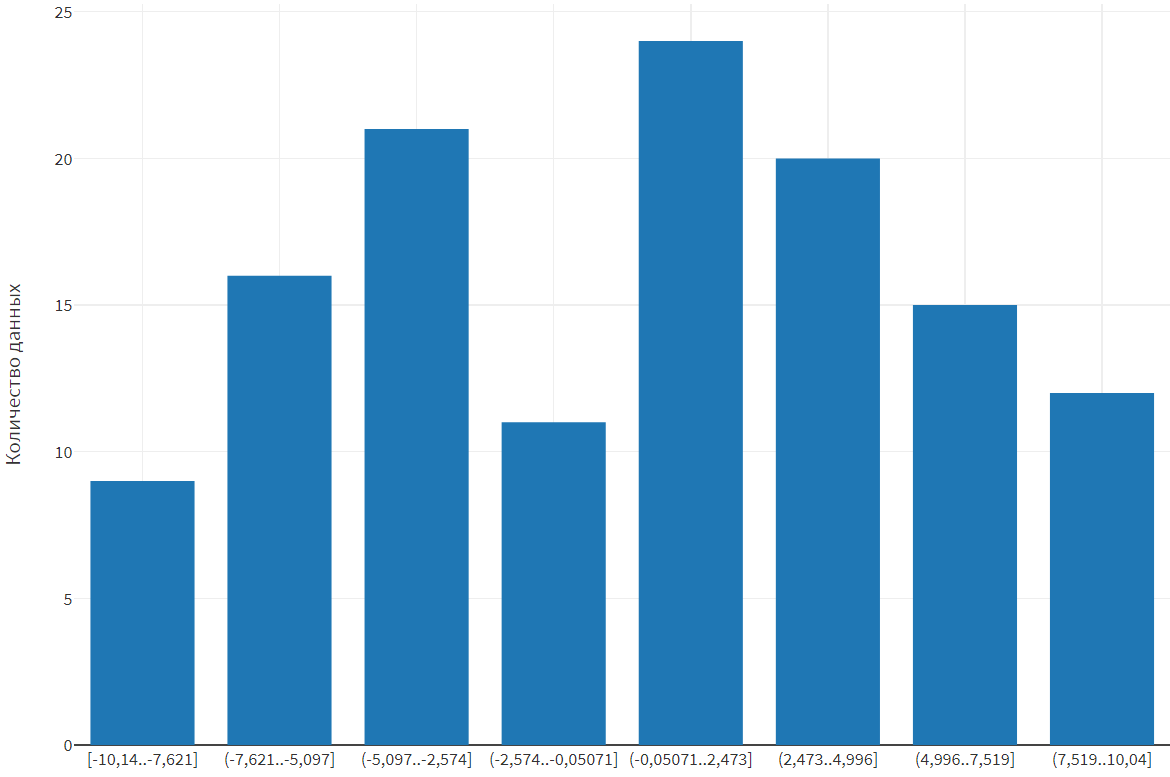
Рисунок 11 – Гистограмма для пятого набора данных
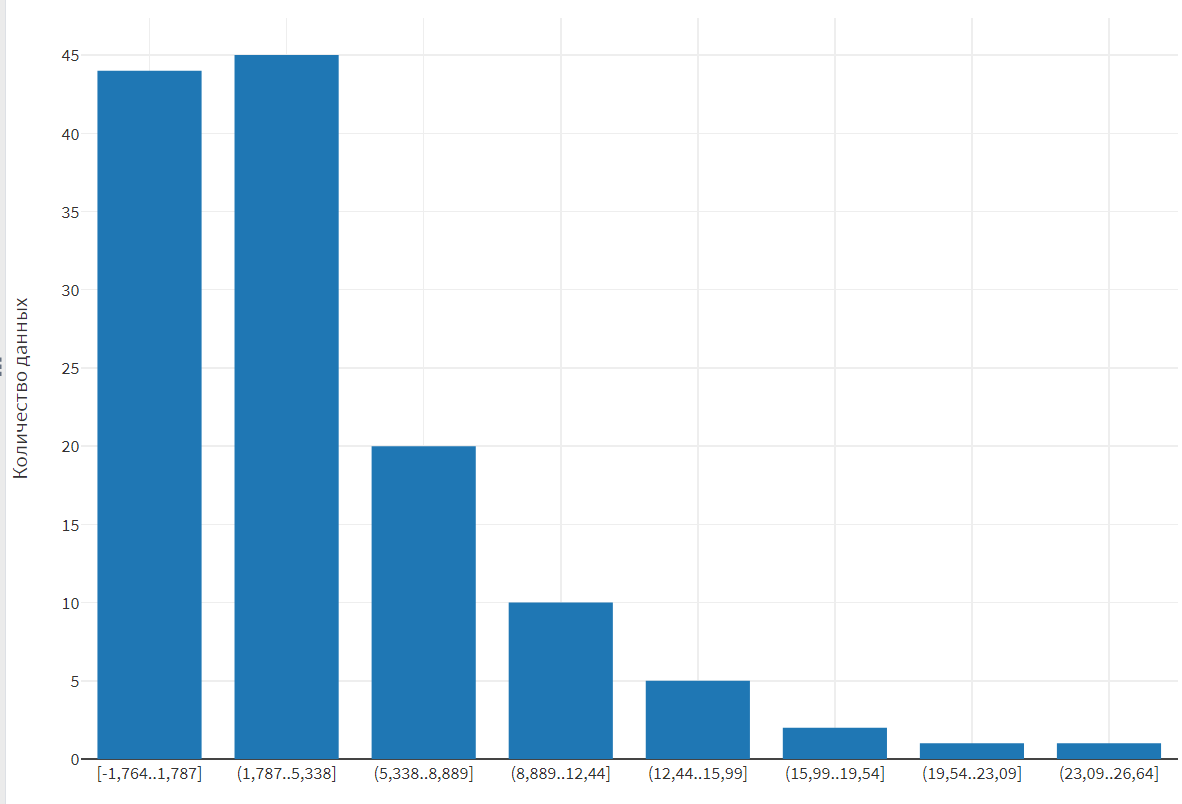
Рисунок 12 – Гистограмма для шестого набора данных
Далее
была найдена точечная оценка математического
ожидания по формуле:
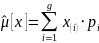 .
Затем
были рассчитаны точечные оценки дисперсии
по формуле:
.
Затем
были рассчитаны точечные оценки дисперсии
по формуле:
 .
Квадратный корень из оценки дисперсии
дает оценку среднеквадратического
отклонения. Все расчеты были сделаны с
помощью узлов «Калькулятор» и
«Группировка». Результаты представлены
в Таблице 1.
.
Квадратный корень из оценки дисперсии
дает оценку среднеквадратического
отклонения. Все расчеты были сделаны с
помощью узлов «Калькулятор» и
«Группировка». Результаты представлены
в Таблице 1.
Таблица 1 – Точечные оценки параметров генеральной совокупности имеющихся выборок
№ выборки |
|
|
|
1 |
-1,06 |
5,98 |
2,45 |
2 |
-1,55 |
4,13 |
2,03 |
3 |
3,52 |
24,87 |
4,99 |
4 |
-1,34 |
11,22 |
3,35 |
5 |
0,11 |
27,15 |
5,21 |
6 |
4,42 |
20,31 |
4,51 |
Принадлежность
выборок к известному распределению
была определена при помощи критерия
согласия Пирсона:
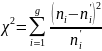 ,
,
где 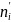 — теоретические частоты попадания в
i-ый интервал.
— теоретические частоты попадания в
i-ый интервал.
Теоретическая частота — это количество элементов из предполагаемого нами распределения, попавших в данный интервал. При этом в качестве параметров теоретического распределения используются рассчитанные нами ранее их точечные оценки. Из этого следует формула для расчёта теоретических частот:
|
|
|
где 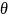 — параметры теоретического распределения;
— параметры теоретического распределения;
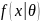 — функция
плотности теоретического распределения;
— функция
плотности теоретического распределения;
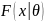 — функция
вероятности теоретического распределения.
— функция
вероятности теоретического распределения.
Рассчитанные теоретические частоты, значения критерия Пирсона, критические значения и сделанные на основе этого выводы представлены в Таблице 2.
Таблица 2 — Гипотезы, значения критериев и выводы, сделанные на их основе
Выборка
№ 1. H0:
|
||||
|
|
|
|
Вывод |
1 |
0.67 |
5.24 |
7.82 |
|
1 |
3.17 |
|||
8 |
7.88 |
|||
15 |
10.24 |
|||
5 |
6.98 |
|||
2 |
2.49 |
|||
Выборка
№ 1. H0:
|
||||
|
|
|
|
Вывод |
1 |
5.33 |
18.25 |
7.82 |
|
1 |
5.33 |
|||
8 |
5.33 |
|||
15 |
5.33 |
|||
5 |
5.33 |
|||
2 |
5.33 |
|||
Выборка № 2. H0: |
||||
|
|
|
|
Вывод |
4 |
5.33 |
2.88 |
7.82 |
, принимается H0 о том, что выборка распределяется по равномерному закону. |
6 |
5.33 |
|||
7 |
5.33 |
|||
2 |
5.33 |
|||
9 |
5.33 |
|||
4 |
5.33 |
|||
Выборка № 2. H0: |
||||
|
|
|
|
Вывод |
4 |
2.56 |
10.4 |
7.82 |
, отвергается H0 о том, что выборка распределяется по нормальному закону. |
6 |
4.87 |
|||
7 |
6.79 |
|||
2 |
6.92 |
|||
9 |
5.17 |
|||
4 |
2.82 |
|||
Выборка
№ 3. H0:
|
||||
|
|
|
|
Вывод |
19 |
21.15 |
8.548 |
9.488 |
, принимается H0 о том, что выборка распределяется по экспоненциальному закону. |
10 |
6.72 |
|||
2 |
2.13 |
|||
0 |
0.68 |
|||
0 |
0.22 |
|||
1 |
0.07 |
|||
Выборка № 3. H0: |
||||
|
|
|
|
Вывод |
19 |
11.72 |
24.53 |
7.81 |
, отвергается H0 о том, что выборка распределяется по нормальному закону. |
10 |
10.12 |
|||
2 |
3.4 |
|||
0 |
0.44 |
|||
0 |
0.22 |
|||
1 |
0.07 |
|||
Выборка № 4. H0: |
||||
|
|
|
|
Вывод |
2 |
6 |
3.907 |
11.07 |
, принимается H0 о том, что выборка распределяется по нормальному закону. |
16 |
15.44 |
|||
31 |
26.92 |
|||
33 |
31.81 |
|||
29 |
25.49 |
|||
12 |
13.84 |
|||
4 |
5.09
|
|||
1 |
1.27 |
|||
Выборка № 4. H0: |
||||
|
|
|
|
Вывод |
2 |
16 |
51.25 |
11.07 |
, отвергается H0 о том, что выборка распределяется по равномерному закону. |
16 |
16 |
|||
31 |
16 |
|||
33 |
16 |
|||
29 |
16 |
|||
12 |
16 |
|||
4 |
16 |
|||
1 |
16 |
|||
Выборка № 5. H0: |
||||
|
|
|
|
Вывод |
9 |
16 |
5.13 |
11.07 |
, принимается H0 о том, что выборка распределяется по равномерному закону. |
16 |
16 |
|||
21 |
16 |
|||
11 |
16 |
|||
24 |
16 |
|||
20 |
16 |
|||
15 |
16 |
|||
12 |
16 |
|||
Выборка № 5. H0: |
||||
|
|
|
|
Вывод |
9 |
6.65 |
36.45 |
11.07 |
, отвергается H0 о том, что выборка распределяется по нормальному закону. |
16 |
11.76 |
|||
21 |
17.29 |
|||
11 |
21.16 |
|||
24 |
21.56 |
|||
20 |
18.28 |
|||
15 |
12.9 |
|||
12 |
7.58 |
|||
Выборка № 6. H0: |
||||
|
|
|
|
Вывод |
44 |
63.65 |
3.44 |
12.59 |
, принимается H0 о том, что выборка распределяется по экспоненциальному закону. |
45 |
31.92 |
|||
20 |
16.01 |
|||
10 |
8.03 |
|||
5 |
4.03 |
|||
2 |
2.02 |
|||
1 |
1.01 |
|||
1 |
0.51 |
|||
Выборка № 6. H0: |
||||
|
|
|
|
Вывод |
44 |
16 |
248.62 |
11.07 |
, отвергается H0 о том, что выборка распределяется по равномерному закону. |
45 |
16 |
|||
20 |
16 |
|||
10 |
16 |
|||
5 |
16 |
|||
2 |
16 |
|||
1 |
16 |
|||
1 |
16 |
|||
Проверим гипотезу о распределении выборки при помощи анаморфоз.
Анаморфоза нормального распределения представлена в формуле:
|
|
|
В
данном случае при построении анаморфозы
нормального распределения
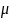 заменяется точечной, полученной ранее.
заменяется точечной, полученной ранее.
Анаморфоза равномерного распределения представлена в формуле:
|
|
|
Анаморфоза экспоненциального распределения представлена в формуле:
|
|
|
Соответствующие анаморфозы, построенные для каждой из выборок, представлены на Рисунках 13-18.
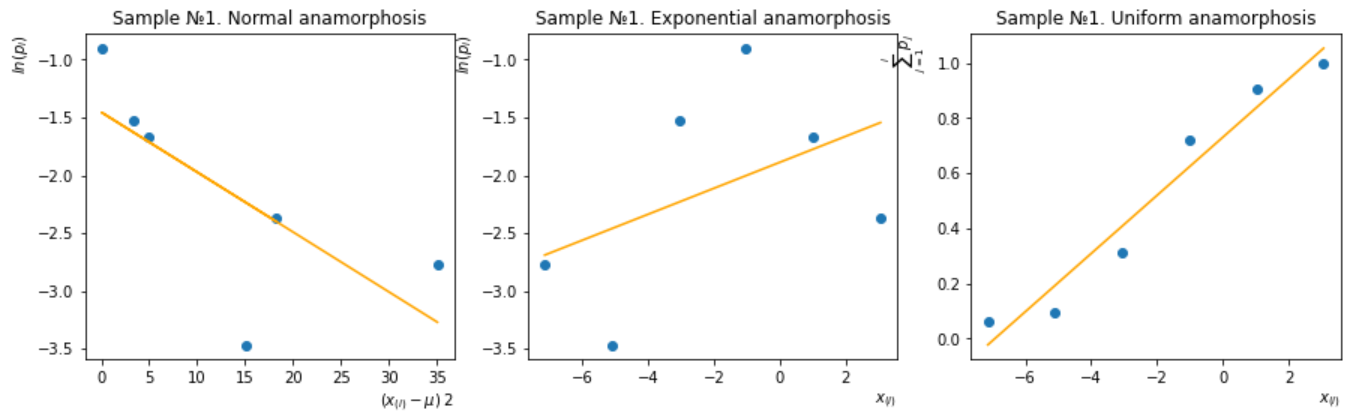
Рисунок 13 – Метод анаморфоз для первой группы
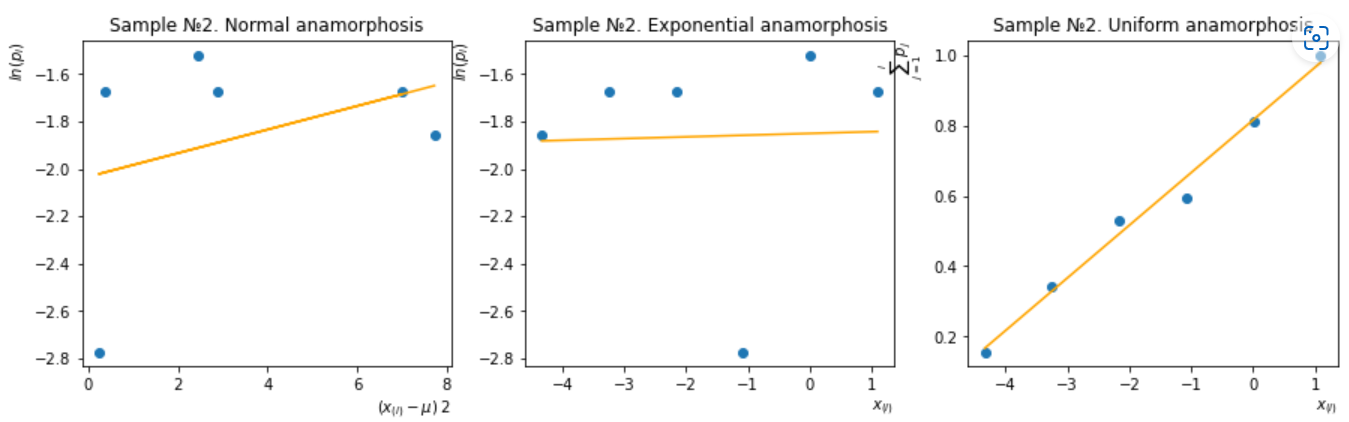
Рисунок 14 – Метод анаморфоз для второй группы
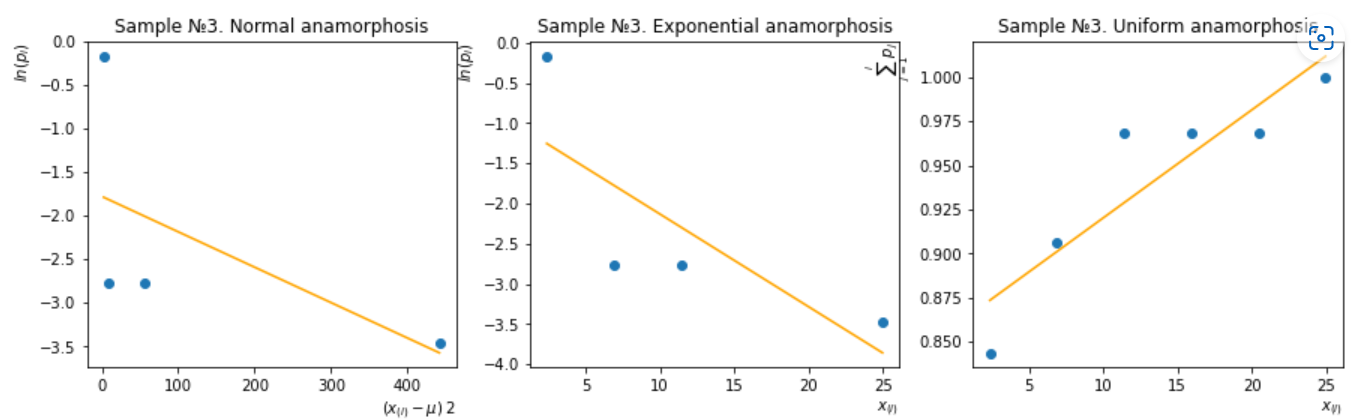
Рисунок 15 – Метод анаморфоз для третьей группы
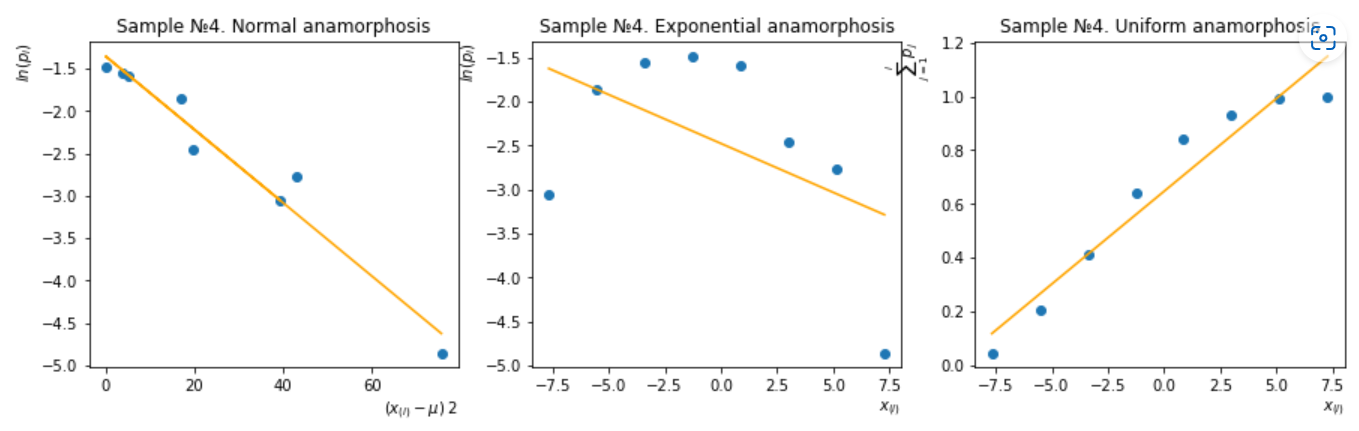
Рисунок 16 – Метод анаморфоз для четвертой группы
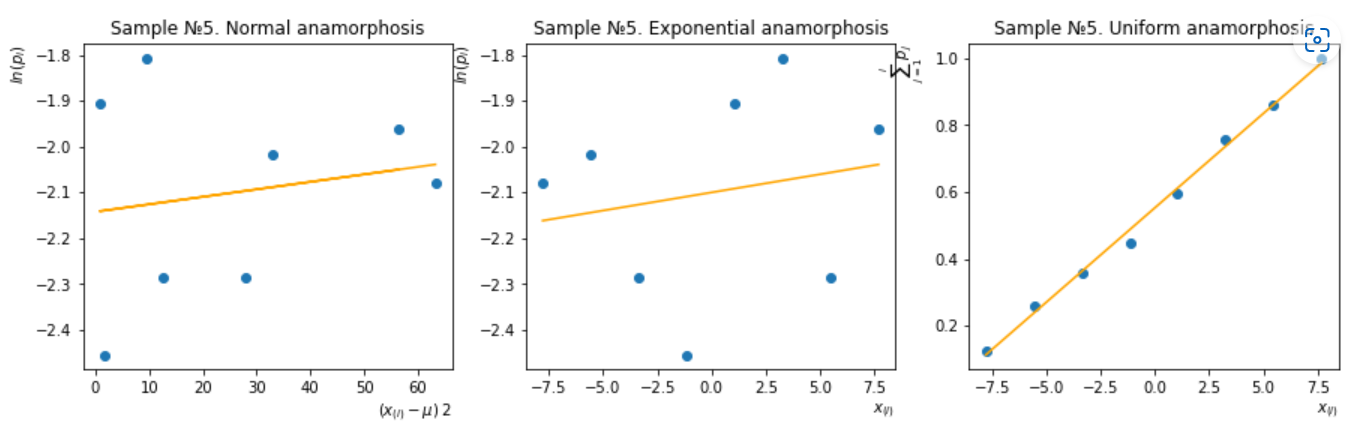
Рисунок 17 – Метод анаморфоз для пятой группы
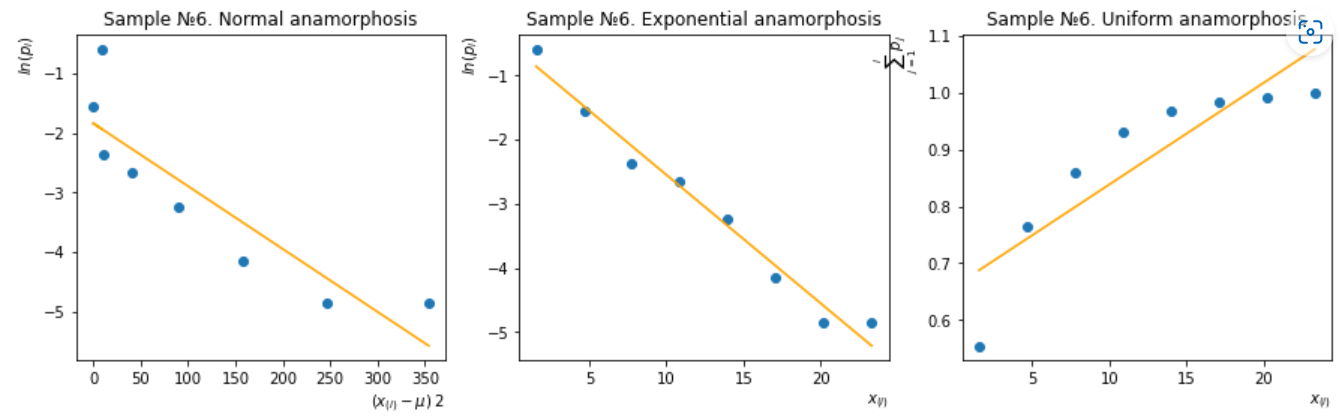
Рисунок 18 – Метод анаморфоз для шестой группы
Итак, наибольшее спрямление имеют выборки:
Первая группа – анаморфоза нормального распределения.
Вторая группа – анаморфоза равномерного распределения.
Третья группа – анаморфоза экспоненциального распределения.
Четвертая группа – анаморфоза нормального распределения.
Пятая группа – анаморфоза равномерного распределения.
Шестая группа – анаморфоза экспоненциального распределения.
На основе этих предположений получаем гипотезы, представленные в Таблице 3:
Таблица 3 — Гипотезы, сделанные на основе графиков анаморфоз
№ выборки |
H0 |
H1 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|



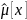
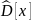
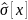
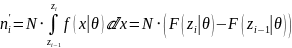
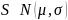
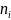
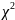
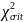
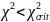 ,
принимается H0
о том, что выборка распределяется по
нормальному закону.
,
принимается H0
о том, что выборка распределяется по
нормальному закону.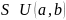
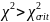 ,
отвергается H0
о том, что выборка распределяется по
равномерному закону.
,
отвергается H0
о том, что выборка распределяется по
равномерному закону.