Вопросы к зкзамену Клюев

В О П Р О С Ы

к экзамену (зачёту) по курсам "Прикладная теория информации" и

"Теория информации, данные, знания"

Билет 1

Определение случайного процесса. Понятие статистического ансамбля. Вероятностное описание случайного процесса с помощью многомерных плотностей вероятности. Основные свойства многомерных плотностей вероятности случайного процесса

Определение 1. Если для каждого значения t зависимая переменная x представляет собой

случайную величину, то говорят, что х=x(t) есть случайная функция времени или случайный

процесс.

Определение 2. Случайный процесс (случайная функция времени) x(t) – это есть некое множество детерминированных функций (реализаций случайного процесса), на котором задана вероятностная мера.

Статистический ансамбль представляет собой бесконечный набор реализаций случайного процесса, каждая из которых управляется одинаковыми вероятностными законами. Каждый элемент ансамбля соответствует одной возможной реализации случайного процесса.

Вероятностное описание случайного процесса с помощью многомерных плотностей вероятности: Многомерные плотности вероятности случайного процесса описываются функциями, которые учитывают все возможные реализации процесса и вероятность их появления. Для полного описания необходимо знать одномерные плотности вероятности, совместные плотности вероятности для нескольких моментов времени.

Основные свойства многомерных плотностей вероятности случайного процесса:

Билет 2

Двумерная условная плотность вероятности случайного процесса и ее основные свойства. Зависимость условной плотности вероятности от разности времен для процесса с конечным вероятностным последействием. Многомерные условные плотности вероятности, их свойства и связь с многомерными безусловными плотностями вероятности.

Условная плотность вероятности описывает вероятность нахождения случайного процесса в определенном состоянии при условии, что он был в другом состоянии в другой момент времени W(x₁,t₁; x₂,t₂)=W(x₁,t₁)×W(x₂,t₂ /x₁,t₁).

Физический смысл: W(x₂, t₂/x₁, t₁)dx₂ - есть условная вероятность того, что значение случайной величины х(t₂) лежит в интервале [х₂, х₂+dх₂], если в момент времени t₁ случайный процесс имел значение в интервале [х₁, х₁+dх₁]

Основные свойства условной плотности вероятности:

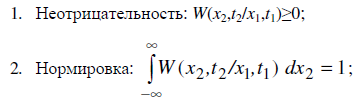
Зависимость от разности времен: для процессов с конечным вероятностным последействием условная плотность вероятности зависит только от разности времен. t=t2-t1

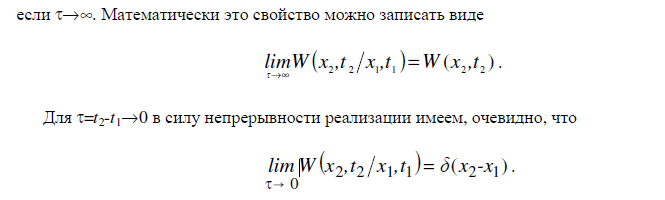
Связь с многомерными безусловными плотностями вероятности: Многомерные условные плотности вероятности могут быть выражены через многомерные безусловные плотности вероятности, используя формулу Байеса.

W(x1​,t1​;x2​,t2​;…)=∫W(x1​,t1​;x2​,t2​;…∣x0​,t0​)W(x0​,t0​)dx0​

Билет 3

Классификация случайных процессов по их вероятностному последействию. Совершенно случайные процессы и марковские процессы, их описание. Уравнение Смолуховского для условной плотности вероятности марковского процесса.

Классификация случайных процессов по вероятностному последействию: Случайные процессы можно классифицировать по тому, как текущее состояние процесса влияет на его будущее состояние:

1. Совершенно случайные процессы – это такой случайный процесс, значения которого в любые несовпадающие моменты времени t1,…,tn статистически независимы.

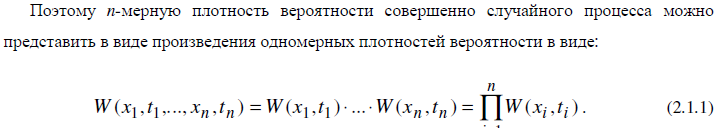
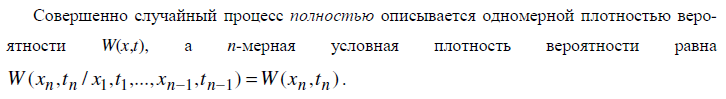
2. Марковские случайные процессы - случайный процесс х(t), у которого условная n-мерная плотность вероятности зависит только от последнего фиксированного значения для любых упорядоченных моментов времени t1 < t2 < ... < tn

Марковский случайный процесс называют еще случайным процессом без последействия, то есть если точно известно состояние марковского процесса в настоящий момент времени, то его будущее состояние не зависит от всех прошлых моментов времени.

n-мерная плотность вероятности для марковского процесса

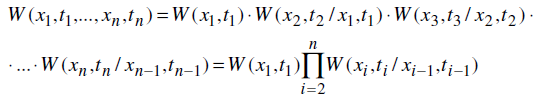
Это означает, что для полного описания марковского процесса достаточно знать одномерное распределение и условную плотность вероятности второго порядка.

Условные плотности вероятности для марковских процессов часто называются вероятностями перехода, поскольку они имеют смысл вероятности перехода с одного уровня х0 на другой уровень х1.

Уравнение Смолуховского. Условная плотность вероятности для марковского процесса удовлетворяет уравнению Смолуховского, которое выражает тот факт, что вероятности перехода для каких-то трех последовательных моментов времени должны быть определенным образом согласованы между собой.

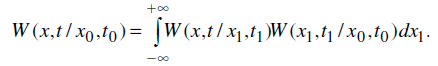(2.2.3)

Ограничение, которое налагается уравнением Смолуховского на допустимый вид условных плотностей вероятности W: интегрирование по х1 произведения двух условных плотностей вероятности должно снова давать условную плотность вероятности W и должно автоматически исключать зависимость результата от промежуточного момента времени t1, от которого зависит подынтегральная функция в (2.2.3) [1].

Уравнение Смолуховского (2.2.3) справедливо для любого марковского процесса.

3. Квазидетерминированные случайные процессы

Квазидетерминированным называется процесс, реализации которого описываются функцией времени заданного вида, но содержащей в себе один или несколько случайных параметров (величин).

Для детерминированного процесса можно записать условную плотность вероятности в виде:

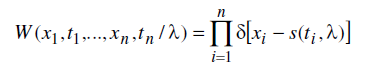
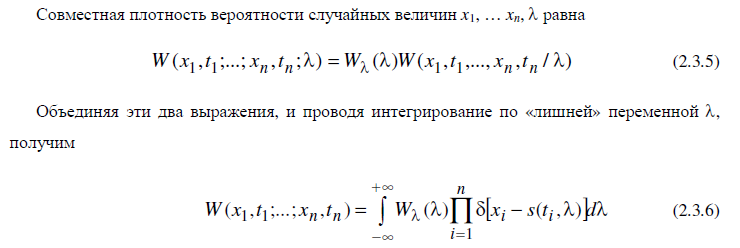
Билет 4

Детерминированные и квазидетерминированные процессы, их описание в рамках теории случайных процессов, выражения для n-мерных плотностей вероятности.

Детерминированные процессы описываются точными математическими функциями без случайных компонентов.

Пусть x(t)=s(t) - детерминированная функция. В качестве примера рассмотрим детерминированный процесс x(t) = A₀ cos(w₀t + j₀ ) , где амплитуда A0, начальная фаза j0 и частота w0 являются постоянными величинами. Ансамбль детерминированного процесса состоит из одной и той же реализации. Поэтому вероятность попасть в момент времени t1 в точку s(t1) будет равна единице. Следовательно, одномерная плотность вероятности будет равна W(x₁, t₁) = d[x₁ − s(t₁)], где d(х) – дельта-функция Дирака.

Рассуждая аналогично, для многомерной плотности вероятности получим, что

Квазидетерминированным называется процесс, реализации которого описываются функцией времени заданного вида, но содержащей в себе один или несколько случайных параметров (величин).

Для детерминированного процесса можно записать условную плотность вероятности в виде:

Многомерная плотность вероятности (2.3.6)

Билет 5

Квазигармонический процесс X(t) = A₀cos(₀t + ) со случайной начальной фазой, равномерно распределенной в интервале [-,]. Его одномерная плотность вероятности.

Найдем плотность вероятности квазидетерминированного случайного процесса (2.3.3). Для этого нужно найти плотность вероятности для значений x в некоторый фиксированный момент времени t, если известна плотность вероятности для начальных фаз φ. Ясно, что начальные фазы могут принимать значения только в интервале (– π, π).

Билет 6

Многомерная характеристическая функция случайного процесса и ее основные свойства.

Характеристическая функция является функцией n переменных u1, u2,…, un и зависит от n

параметров t1,t1,…,tn.

Билет 7

Моментные функции случайного процесса. Среднее значение и корреляционная функция. Связь моментных функций с характеристической функцией.

В качестве характеристик случайных процессов, более простых, чем плотности вероятности и характеристические функции, широко используются моментные и кумулянтные функции. Наиболее распространенными статистическими характеристиками являются:

Моментные функции случайного процесса включают в себя его среднее значение и корреляционную функцию.

Связь моментных функций с характеристической функцией

Задание n-мерной характеристической функции эквивалентно заданию всех n-мерных моментных функций любого порядка s=1,2,…,¥ при условии, что эти моментные функции существуют и ряд (3.2.11) сходится.

Билет 8

Кумулянтные функции случайного процесса, их связь с характеристической функцией. Связь между кумулянтными и моментными функциями (на примере функций 1-го и 2-го порядка).

Кумулянтные функции описывают статистические свойства случайного процесса и связаны с характеристической функцией. Задание всех кумулянтных функций заданной размерности полностью описывает случайный процесс, поскольку эквивалентно заданию характеристической функции или плотности вероятностей заданной размерности.

Мы найдем выражение только для первых двух кумулянтных функций через моментные функции из их определения

Следовательно, кумулянтная функция первого порядка в некоторый момент времени tk представляет собой среднее значение случайного процесса в этот момент времени.

В результате последовательных преобразований, а, также учитывая свойство нормировки

характеристической функции, получим, что К₂(tk1, tk2)=

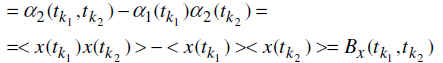
Кумулянтная функция второго порядка называется ковариационной функцией Bx[t1,t2]

случайного процесса. И при совпадающих моментах времени t1 = t2 = t корреляционная функция

является дисперсией случайного процесса.

Билет 9

Ковариационная функция случайного процесса. Дисперсия. Понятия некоррелированности и статистической независимости двух значений случайного процесса. Коэффициент корреляции.

Ковариационная функция B_x[t₁,t₂] – это кумулянтная функция второго порядка. Она равна корреляционной функции минус произведение средних значений

Понятия некоррелированности и статистической независимости двух значений случайного процесса

Статистическая независимость: Две случайные величины называются независимыми, если вероятностное распределение одного значения не зависит от другого.

Коэффициент корреляции между X(t1​) и X(t2​) определяется как:

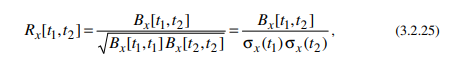
Билет 10

Гауссовские случайные процессы, их n-мерная характеристическая функция и одномерная плотность вероятности. Информация, необходимая для полного описания гауссовского случайного процесса.

Гауссовские случайные процессы — это процессы, такой что любой конечный набор этих случайных величин имеет многомерное нормальное распределение, то есть любая конечная линейная комбинация из них нормально распределена.

Гауссовым называется случайный процесс, у которого все кумулянтные функции высших порядков, начиная с третьего, равны нулю.

Информация, необходимая для полного описания гауссовского случайного процесса

Билет 11

Основные свойства гауссовских случайных процессов

Билет 12

Стационарные случайные процессы. Понятия стационарности в узком и широком смысле, их взаимоотношение.

Стационарные случайные процессы

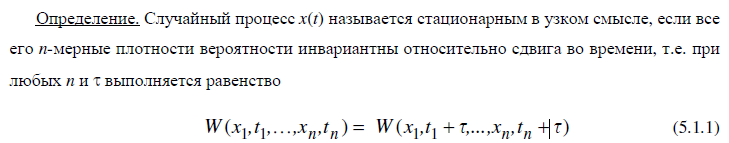
Из стационарности в узком смысле следует стационарность в широком смысле, но не наоборот.

Для гауссовых процессов понятия стационарности в узком и широком смыслах совпадают, поскольку их n-мерные плотности вероятности полностью определяются средним значением и ковариационной функцией.

Для случайных марковских процессов понятия стационарности в узком и широком смысле являются близкими, но не совпадают. Обычно если вводят стационарный марковский процесс, то в узком смысле.

Совершенно случайный процесс стационарен в узком смысле, если W(x,t)=W(x).

Билет 13

Эргодичность случайных процессов. Необходимые и достаточные условия эргодичности по отношению к среднему значению.

Эргодичность случайных процессов

Процесс называется эргодичным, если его временные средние совпадают с ансамблевыми средними.

Необходимые и достаточные условия эргодичности по отношению к среднему значению

Определение: говорят, что случайный процесс x(t) обладает эргодическим свойством относительно среднего значения, если среднее по времени при сходится к среднему по статистическому ансамблю, то есть

Стационарность является необходимым условием для эргодичности, но не достаточным!

Для того, чтобы стационарный в широком смысле случайный процесс х(t) был эргодичен по отношению к среднему значению, необходимо и достаточно, чтобы выполнялось условие

, где В_х - ковариационная функция случайного процесса

Билет 14

Количество информации. Основные свойства информации.

Количество информации, это мера снятой неопределенности сообщения. В контексте информационной теории это понятие используется для измерения количества известной информации, которое содержится в сообщении или событии.

Основные свойства информации

1. Неотрицательность: количество информации не может быть отрицательным.

2. Монотонность: количество информации возрастает с уменьшением вероятности наступления события. То есть, чем менее вероятное событие, тем больше информации оно содержит.

3. Аддитивность для независимых источников: если информация поступает от различных независимых источников, общее количество информации равно сумме информаций от каждого источника.

Билет 15

Энтропия — это физическая величина, которая измеряет степень неопределенности системы. Чем выше уровень энтропии, тем выше степень беспорядка в системе.

1. Энтропия 𝐻(𝑋) ≥ 0 поскольку pi удовлетворяет неравенству 0 ≤ 𝑝𝑖 ≤ 1.

𝐻(𝑋) = 0 тогда и только тогда, когда одна из вероятностей равна 1 при всех остальных, равных нулю (мера недостоверности наверняка осуществимого события равна 0).

2. Энтропия максимальна, когда все состояния источника равновероятны. При равновероятности состояний предсказание об осуществимости какого-то конкретного из них максимально недостоверно.

3. Пусть случайные события A и B независимы. Тогда энтропия произведения (совместного осуществления) событий A⋅B равна сумме энтропий перемножаемых событий: H(A⋅B)=H(A)+H(B).

При равномерном распределении (равновероятностном появлении символа): 𝑝_𝑖 =1/𝑚_𝑥

Тогда энтропия: 𝐻(𝑋) <= log 𝑚_𝑥

Билет 16

Дискретные источники сообщений и их описание. Эргодические источники. Марковские источники сообщений.

Дискретными называют источники информации, сообщения которых представляют собой последовательности четко различимых знаков, букв, цифр, символов, принадлежащих конечному упорядоченному множеству.

Источник будем называть эргодическим, если его вероятностные параметры можно оценить по одной достаточно длинной реализации, которую он вырабатывает.

При неограниченном возрастании длины реализации (n) оценка параметра (результат измерения) совпадает с его истинным значением с вероятностью, равной единице.

Марковские источники сообщений

Марковский источник описывается матрицей переходных вероятностей между символами.

Билет 17

Экономное кодирование. Алгоритм кодирования по методу Шеннона-Фэно

Метод Шеннона-Фэно основывается на распределении символов по их вероятностям:

1. Отсортировать символы по убыванию вероятности их появления.

2. Разделить символы на две примерно равные по вероятности группы, т.е. сумма вероятностей одной группы была примерно равна сумме вероятностей другой.

3. Присвоить первой группе бит - '0', а второй - '1'.

4. Рекурсивно применить этот процесс к каждой группе, разбивая ее на подгруппы и назначая им соответствующие битовые значения.

5. Продолжать этот процесс до достижения требуемой точности или минимального размера блока. В результате каждому сообщению будет соответствовать своя последовательность из нулей и единиц, т.е. кодовое слово

Билет 18

Экономное кодирование. Алгоритм кодирования по методу Хаффмена

Метод Хаффмена строит дерево кодирования

1. Каждый символ сообщения рассматривается как отдельный узел с его вероятностью. Этот список узлов можно организовать в виде дерева, где каждый узел содержит символ и его вероятность.

2. Построим двоичное дерево, объединяя два узла с наименьшими вероятностями появления. Этот процесс повторяется до тех пор, пока не будет построено полное дерево. При каждом шаге новый узел добавляется в список, а два самых маловероятных узла удаляются.

3. Когда дерево построено, присвоим каждому символу код, представленный последовательностью битов от корня до соответствующего листа. При этом левому потомку присваивается '0', а правому - '1'. Это обеспечивает, что коды символов с более высокой вероятностью будут более короткими, что способствует эффективному сжатию.

4. Каждый символ будет иметь код, представленный последовательностью битов от корня до соответствующего листа.