1 Часть. Электротехника. Постоянный ток

1. Линейные и нелинейные, разветвленные и неразветвленные электрические цепи.

Электрической цепью называется технически обоснованная совокупность её компонентов, соединённых между собой определённым образом.

Компонентами или элементами электрической цепи являются:

• источники электрической энергии,

• активные сопротивления,

• реактивные сопротивления,

• различные электронные приборы.

Линейные элементы - это элементы электрической цепи, для которых зависимость тока от напряжения I(U) постоянна. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.

Нелинейным элементом электрической цепи называют элемент ВАХ которого отлична от линейной. Если цепь содержит хотя бы один нелинейный элемент, то цепь именуется нелинейной электрической цепью.

Цепь, состоящая из 2-х и более ветвей, называется.

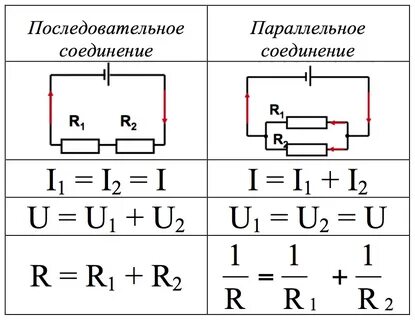
2. Законы Ома для участка цепи.

Для пассивного

Для активного

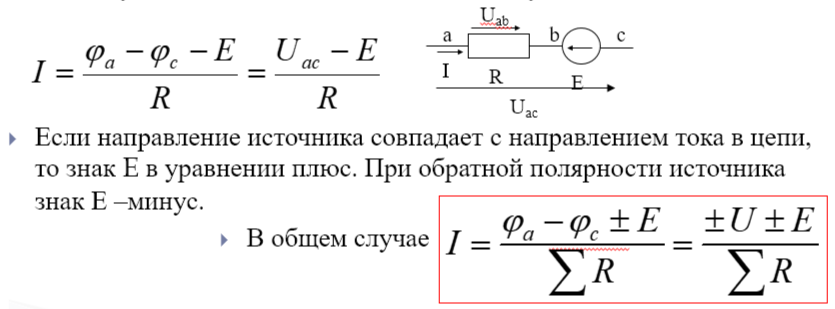
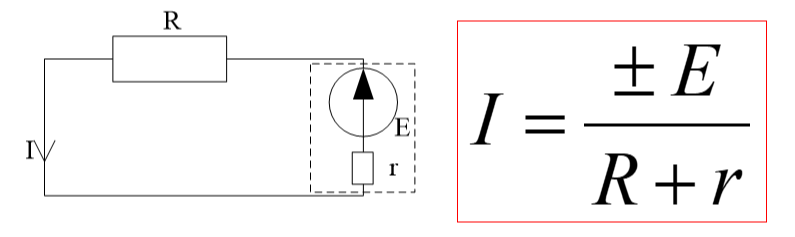
Для замкнутого контура

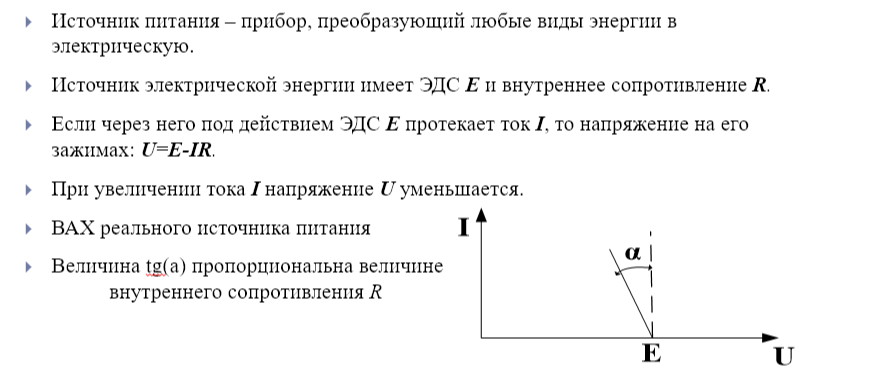
3. Вольтамперные характеристики элементов электрических цепей

Зависимость тока, протекающего по сопротивлению от напряжения на этом сопротивлении, называется вольтамперной характеристикой (ВАХ) элемента электрической цепи.

4. Источник ЭДС и источник тока.

5. Законы Кирхгофа

1 Закон - Алгебраическая сумма токов, подтекающих к любому схему равна нулю.

• Сумма втекающих в любой узел токов равна сумме токов, утекающих от этого узла.

• По первому закону Кирхгофа можно составить уравнение, где - количество узлов в схеме.

• Физически, первый закон Кирхгофа означает, что заряды ни в одном из узлов не накапливаются.

2. Закон - Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме эдс вдоль того же контура.

• Алгебраическая сумма напряжений в любом замкнутом контуре равна нулю

• По второму закону Кирхгофа можно построить уравнений: , где

• N_в - число ветвей схемы;

• N_{в ит} - число ветвей, содержащих источник тока.

• Для контура с источником тока второй закон Кирхгофа не записывают!!!

1 РГР

1. Определяем кол-во узлов и ветвей, а затем уравнений: |

2. Выбрать контуры и расставить токи.

3. Записываем систему уравнений.

4. Проверяем уравнения и число неизвестных.

5. Решаем мтд Гаусса.

6. Проверяем по 1 зк Кирхгофа накопление тока в узлах.

6. Метод контурных токов

• Для расчета схема сложной электрической цепи разбивается на контуры по кратчайшим путям, т.е. выбираются контуры-ячейки.

• Токи в ветвях, принадлежащих более, чем одному контуру, определяются на основе первого закона Кирхгофа через контурные токи. В результате происходит понижение размерности задачи за счет сокращения числа неизвестных токов.

• Контурные уравнения строятся только на основе второго закона Кирхгофа.

КОНТУРНЫЕ ВЕЛИЧИНЫ

• Контурное сопротивление – сумма всех сопротивлений, входящих в контур (R_ii).

• Общее (взаимное) сопротивление двух контуров – сумма сопротивлений, лежащих на общей ветви двух контуров. Знак общего сопротивления определяется исходя из взаимного направления контурных токов по общей ветви – если контурные токи сонаправлены, то «+», если противонаправлены, то «-» (R_ij).

• Контурный ток – ток, замыкающийся в рамках рассматриваемого контура (I_ii).

• Контурная ЭДС – алгебраическая сумма ЭДС выбранного контура, взятая относительно направления контурного тока (E_ii).

7. Метод узловых потенциалов -

• Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы.

• Ток в любой ветви схемы можно найти по закону Ома. Для того чтобы можно было применить закон Ома, необходимо знать значение потенциалов узлов схемы.

• Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по I закону Кирхгофа.

УЗЛОВЫЕ ВЕЛИЧИНЫ

• Узловой ток (J_ii) формируется всеми источниками питания, подключенными к текущему узлу. Причем, если источник питания направлен к узлу, то его вклад положительный, если от узла – отрицательный.

• Собственная проводимость узла (G_ii) – сумма проводимостей всех ветвей, подключенных к текущему (i-му) узлу.

• Общая (взаимная) проводимость i-го и j-го узлов (G_ij = G_ji) – сумма проводимостей ветвей, непосредственно соединяющих i-й и j-й узлы, взятая со знаком «–».

• Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят!

• Узловое уравнение в общем виде для узла с номером i в схеме, состоящей из n узлов:

8. Метод двух узлов

• Метод двух узлов – частный случай метода узловых потенциалов.

• Применяется в схемах, где несколько параллельных ветвей подключено к паре узлов.

• Преимущество этого метода перед другими возрастает с увеличением числа параллельных ветвей электрических цепей.

• Определяется узловое напряжение, что позволяет определять токи в параллельных ветвях на основе закона Ома. 

9. Принцип и метод наложения

• Метод наложения токов (суперпозиции) применяется для расчета сложных электрических цепей постоянного тока с несколькими источниками энергии.

• Наиболее целесообразно применять его при небольшом числе источников.

• По сравнению с другими методами он имеет преимущества в тех случаях, когда не требуется полный расчет цепи, а можно ограничиться, например, определением токов только в некоторых ветвях электрической цепи.

АЛГОРИТМ

1. В методе наложения электрическая цепь с несколькими источниками ЭДС и напряжений заменяется частными электрическими схемами с одним источником.

2. Число частных схем равно числу источников, действующих в электрической цепи.

3. Все источники питания, кроме рассматриваемого, из цепи удаляют, оставляя в только их внутренние сопротивления.

4. В результате расчета каждой частной схемы определяются частичные токи, возникающие под действием данного источника питания.

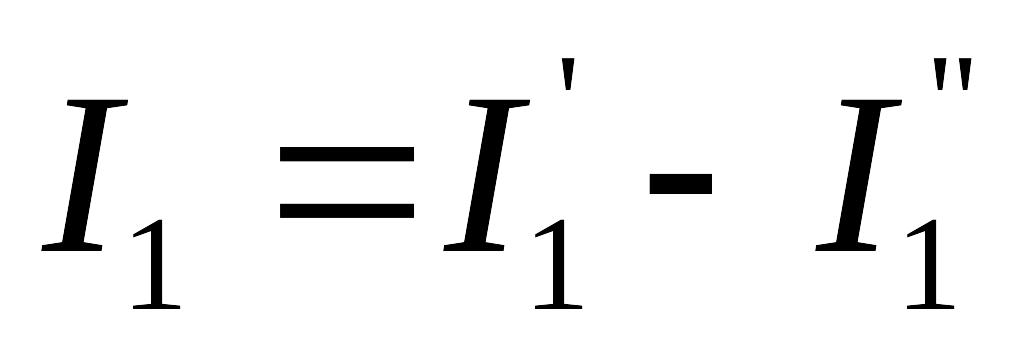
5. З начение токов ветвей исходной схемы определяется алгебраическим суммированием частичных токов в этих ветвях.

10. Метод эквивалентного генератора

• Метод применяется для определения тока или напряжения в отдельной ветви схемы, но не для полного расчета цепи.

• Применяется в случае необходимости подбора параметров нагрузочного элемента.

• Ветвь, характеристики которой требуется определить называется ветвью с нагрузкой.

• В основе метода лежит теорема об активном двухполюснике:

• активный двухполюсник в расчетном отношении можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах двухполюсника, а внутреннее сопротивление равно входному сопротивлению того же двухполюсника, но в схеме которого все источники питания заменены на их внутренние сопротивления.

АЛГОРИТМ

1. Все элементы схемы, за исключением нагрузочной ветви заменяются эквивалентным генератором, характеризующимся внутренним сопротивлением и ЭДС.

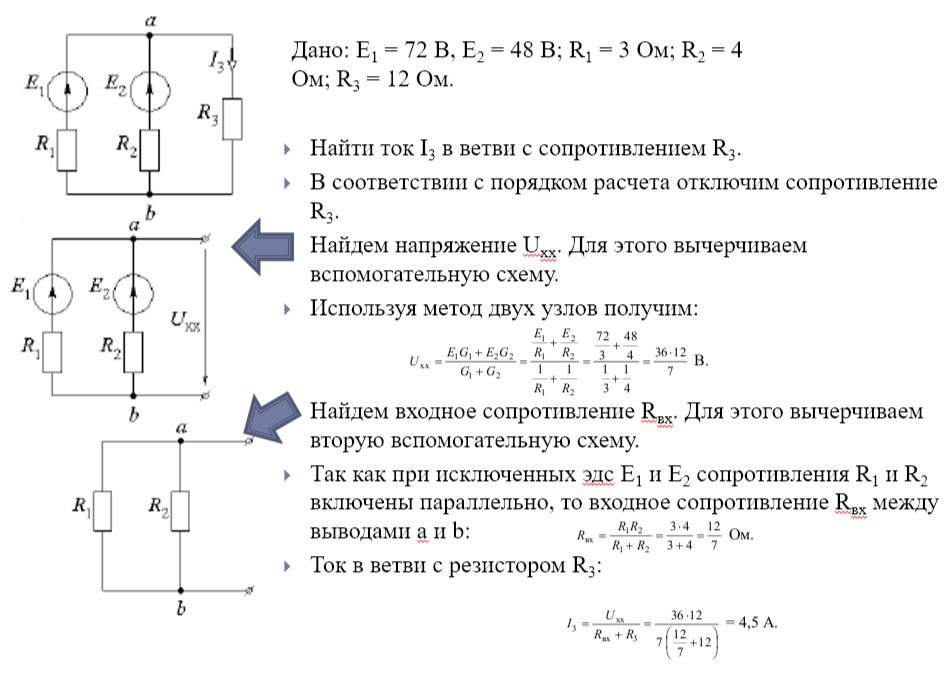
2. Для расчета тока в сопротивлении R следует сначала отключить это сопротивление.

3. При определении параметров эквивалентного генератора расчетным путем необходимо вычертить две схемы.

4. Первая схема служит для определения Uхх = Eэ и отличается от исходной тем, что исследуемая ветвь разрывается. Методом контурных токов, методом уравнений Кирхгофа или другим методом рассчитывают напряжение между точками разрыва.

5. Вторая схема служит для определения Rвх = Rэ; в ней исключаются источники питания (заменяются на внутренние сопротивления) и находится входное сопротивление относительно зажимов выделенной ветви.

6. Если выделенная ветвь содержит источник эдс, то последнюю учитывают при определении Uхх.

7. Рассчитывается искомый ток.