10.3.3. Поняття: штучний нейрон, штучна нейронна мережа, функції активації штучного нейрона (лінійна, порогова, сигмоїдна, радіально-базисна Гауса)
Штучний нейрон (Математичний нейрон Маккалоха — Піттса[en], Формальний нейрон[1]) — вузол штучної нейронної мережі, що є спрощеною моделлю природного нейрона. Математично, штучний нейрон зазвичай представляють як деяку нелінійну функцію від єдиного аргументу — лінійної комбінації всіх вхідних сигналів. Цю функцію називають функцією активації або функцією спрацьовування, передавальною функцією. Отриманий результат посилається на єдиний вихід. Такі штучні нейрони об'єднують в мережі — з'єднують виходи одних нейронів з входами інших. Штучні нейрони та мережі є основними елементами ідеального нейрокомп'ютера.
Біологічний нейрон складається з тіла, діаметром від 3 до 100 мкм, що містить ядро (з великою кількістю ядерних пор) та інші органели (у тому числі сильно розвинений шорсткий ЕПР з активними рибосомами, апарат Гольджі) і відростків. Виділяють два види відростків. Аксон — зазвичай довгий відросток, пристосований для проведення збудження від тіла нейрона. Дендрити — як правило, короткі і сильно розгалужені відростки, які служать головним місцем утворення збуджуючих і гальмівних синапсів (різні нейрони мають різне співвідношення довжини аксона і дендритів). Нейрон може мати кілька дендритів і зазвичай тільки один аксон. Один нейрон може мати зв'язки з десятками тисяч інших нейронів. Кора головного мозку людини містить десятки мільярдів нейронів.
Історія розвитку. Математична модель штучного нейрону була запропонована В. Маккалохом та В. Піттсом разом з моделлю мережі, що складається з цих нейронів. Автори показали, що мережа на таких елементах може виконувати числові і логічні операції[3]. Практично мережа була реалізована Френком Розенблатом в 1958 році як комп'ютерна програма, а згодом як електронний пристрій — перцептрон. Спочатку нейрон міг оперувати тільки з сигналами логічного нуля і логічної одиниці[4], оскільки був побудований на основі біологічного прототипу, який може перебувати тільки в двох станах — збудженому або не збудженому. Розвиток нейронних мереж показав, що для розширення області їхнього застосування необхідно, щоб нейрон міг працювати не тільки з бінарними, але і з безперервними (аналоговими) сигналами. Таке узагальнення моделі нейрона було зроблено Уїдроу і Хоффом[5], які запропонували використовувати логістичну криву як функцію спрацьовування нейрона.
Зв'язки, якими вихідні сигнали одних нейронів надходять на входи інших, часто називають синапсами за аналогією зі зв'язками між біологічними нейронами. Кожен зв'язок характеризується своєю вагою. Зв'язки з позитивною вагою називаються збудливими, а з негативною — гальмівними[6]. Нейрон має один вихід, який часто називають аксоном за аналогією з біологічним прототипом. З єдиного виходу нейрона сигнал може надходити на довільне число входів інших нейронів.
Відмінності між біологічним і штучним нейроном. Нейронні мережі, побудовані на штучних нейронах, виявляють деякі ознаки, які дозволяють зробити припущення про подібність їх структури до структури мозку живих організмів. Тим не менше, навіть на нижчому рівні штучних нейронів існують суттєві відмінності. Наприклад, штучний нейрон є безінерційною системою, тобто сигнал на виході з'являється одночасно з появою сигналів на вході, що зовсім не характерно для біологічного нейрона.
Штучні нейронні мережі (ШНМ, англ. artificial neural network), які зазвичай просто називають нейронними мережами (НМ, англ. neural networks, NN) або нейромережами (англ. neural nets),[1] це обчислювальні системи, натхнені біологічними нейронними мережами, які складають мозок тварин.
ШНМ ґрунтується на сукупності з'єднаних вузлів (англ. units, nodes), які називають штучними нейронами, які приблизно моделюють нейрони біологічного мозку. Кожне з'єднання, як і синапси в біологічному мозку, може передавати сигнал до інших нейронів. Штучний нейрон отримує сигнали, потім обробляє їх і може сигналізувати нейронам, з якими його з'єднано. «Сигнал» у з'єднанні це дійсне число, а вихід кожного нейрона обчислюється деякою нелінійною функцією суми його входів. З'єднання називають ребрами (англ. edges). Нейрони та ребра зазвичай мають вагу[en] (англ. weight), яка підлаштовується в процесі навчання. Вага збільшує або зменшує силу сигналу на з'єднанні. Нейрони можуть мати такий поріг, що сигнал надсилається лише тоді, коли сукупний сигнал перевищує цей поріг.
Як правило, нейрони зібрано в шари (англ. layers). Різні шари можуть виконувати різні перетворення даних свого входу. Сигнали проходять від першого шару (шару входу) до останнього (шару виходу), можливо, після проходження шарами декілька разів.
Тренування. Нейронні мережі навчаються (або, їх тренують) шляхом обробки прикладів, кожен з яких містить відомий «вхід» та «результат», утворюючи ймовірнісно зважені асоціації між ними, які зберігаються в структурі даних самої мережі. Тренування нейронної мережі заданим прикладом зазвичай здійснюють шляхом визначення різниці між обробленим виходом мережі (часто, передбаченням) і цільовим виходом. Ця різниця є похибкою. Потім мережа підлаштовує свої зважені асоціації відповідно до правила навчання і з використанням цього значення похибки. Послідовні підлаштовування призведуть до виробляння нейронною мережею результатів, усе більше схожих на цільові. Після достатньої кількості цих підлаштовувань, тренування можливо припинити на основі певного критерію. Це форма керованого навчання.
Такі системи «навчаються» виконувати завдання, розглядаючи приклади, як правило, без програмування правил для конкретних завдань. Наприклад, у розпізнаванні зображень вони можуть навчитися встановлювати зображення, на яких зображені коти, аналізуючи приклади зображень, мічені[en] вручну як «кіт» та «не кіт», і використовуючи результати для ідентифікування котів на інших зображеннях. Вони роблять це без будь-якого апріорного знання про котів, наприклад, що вони мають хутро, хвости, вуса та котоподібні писки. Натомість, вони автоматично породжують ідентифікаційні характеристики з прикладів, які оброблюють.
Моделі. ШНМ почалися як спроба використати архітектуру людського мозку для виконання завдань, у яких звичайні алгоритми мали невеликий успіх. Незабаром вони переорієнтувалися на покращення емпіричних результатів, відмовившись від спроб залишатися вірними своїм біологічним попередникам. ШНМ мають здатність навчатися нелінійностей та складних зв'язків та моделювати їх. Це досягається тим, що нейрони з'єднуються за різними схемами, що дозволяє виходам одних нейронів стати входом інших. Ця мережа утворює орієнтований зважений граф.
Штучна нейронна мережа складається з імітацій нейронів. Кожен нейрон з'єднано з іншими вузлами (англ. nodes) ланками (англ. links), як біологічне з'єднання аксон—синапс—дендрит. Усі вузли, з'єднані ланками, отримують деякі дані й використовують їх для виконання певних операцій і завдань з даними. Кожна ланка має вагу (англ. weight), що визначає силу впливу одного вузла на інший,[96] дозволяючи вагам обирати сигнал між нейронами.
Штучні нейрони. ШНМ складаються зі штучних нейронів, які концептуально походять від біологічних. Кожен штучний нейрон має входи та видає єдиний вихід, який можливо надсилати багатьом іншим нейронам.[97] Входи (англ. inputs) можуть бути значеннями ознак зразка зовнішніх даних, таких як зображення чи документи, або вони можуть бути виходами інших нейронів. Виходи кінцевих нейронів виходу (англ. output neurons) нейронної мережі завершують завдання, наприклад, розпізнавання об'єкта на зображенні.
Щоби знайти вихід нейрона, ми беремо зважену суму всіх входів, зважених за вагами з'єднань (англ. connection weights) від входів до нейрона. Ми додаємо до цієї суми зміщення (англ. bias).[98] Цю зважену суму іноді називають збудженням (англ. activation). Цю зважену суму потім пропускають крізь (зазвичай нелінійну) передавальну функцію (англ. activation function) для отримання виходу. Первинними входами є зовнішні дані, наприклад зображення та документи. Кінцеві виходи завершують завдання, наприклад, розпізнавання об'єкта на зображенні.
Будова. Нейрони зазвичай впорядковано в кілька шарів (англ. layers), особливо в глибокому навчанні. Нейрони одного шару з'єднуються лише з нейронами безпосередньо попереднього й наступного шарів. Шар, який отримує зовнішні дані, це шар входу (англ. input layer). Шар, який видає кінцевий результат, це шар виходу (англ. output layer). Між ними є нуль або більше прихованих шарів (англ. hidden layers). Використовують також одношарові (англ. single layer) та безшарові (англ. unlayered) мережі. Між двома шарами можливі кілька схем з'єднання. Вони можуть бути «повноз'єднаними» (англ. 'fully connected'), коли кожен нейрон одного шару з'єднується з кожним нейроном наступного шару. Вони можуть бути агрегувальними (англ. pooling), коли група нейронів одного шару з'єднується з одним нейроном наступного шару, знижуючи таким чином кількість нейронів у цьому шарі.[100] Нейрони лише з такими зв'язками утворюють орієнтований ациклічний граф і відомі як мережі прямого поширення (англ. feedforward networks).[101] Крім того, мережі, які дозволяють з'єднання до нейронів у тому же або попередніх шарах, відомі як рекурентні мережі (англ. recurrent networks).
Гіперпараметр (англ. hyperparameter) — це сталий параметр, чиє значення встановлюють перед початком процесу навчання. Значення же параметрів (англ. parameters) виводять шляхом навчання. До прикладів гіперпараметрів належать темп навчання (англ. learning rate), кількість прихованих шарів і розмір пакета.[103] Значення деяких гіперпараметрів можуть залежати від значень інших гіперпараметрів. Наприклад, розмір деяких шарів може залежати від загальної кількості шарів.
Навчання (англ. learning) — це пристосовування мережі для кращого виконання завдання шляхом розгляду вибіркових спостережень. Навчання включає підлаштовування ваг (і, можливо, порогів) мережі для підвищення точності результатів. Це здійснюється шляхом мінімізування спостережуваних похибок. Навчання завершено, якщо розгляд додаткових спостережень не знижує рівня похибки. Навіть після навчання рівень похибки зазвичай не досягає 0. Якщо навіть після навчання рівень похибки занадто високий, зазвичай потрібно змінити будову мережі. Практично це здійснюють шляхом визначення функції витрат (англ. cost function), яку періодично оцінюють протягом навчання. Поки її результат знижується, навчання триває. Витрати часто визначають як статистику, значення якої можливо лише наближувати. Виходи насправді є числами, тож коли похибка низька, різниця між результатом (майже напевно кіт) і правильною відповіддю (кіт) невелика. Навчання намагається знизити загальну відмінність над спостереженнями. Більшість моделей навчання можливо розглядати як пряме застосування теорії оптимізації та статистичного оцінювання.
Темп навчання (англ. learning rate) визначає розмір коригувальних кроків, які здійснює модель для підлаштовування під похибку в кожному спостереженні.[105] Високий темп навчання скорочує тривалість тренування, але з меншою кінцевою точністю, тоді як нижчий темп навчання займає більше часу, але з потенціалом до більшої точності. Такі оптимізації, як Quickprop[en] (укр. «швидпошир»), переважно спрямовані на прискорення мінімізування похибки, тоді як інші вдосконалення переважно намагаються підвищити надійність. Щоби запобігти циклічним коливанням усередині мережі, таким як чергування ваг з'єднань, і покращити швидкість збігання, удосконалення використовують адаптивний темп навчання, який підвищується або знижується належним чином.[106] Концепція імпульсу (англ. momentum) дозволяє зважувати баланс між градієнтом і попередньою зміною так, щоби підлаштовування ваги певною мірою залежало від попередньої зміни. Імпульс, близький до 0, додає ваги градієнтові, тоді як значення, близьке до 1, додає ваги крайній зміні.
Функція витрат. Хоча й можливо визначати функцію витрат ad hoc, вибір часто визначається бажаними властивостями цієї функції (такими як опуклість) або тим, що вона постає з моделі (наприклад, у ймовірнісній моделі апостеріорну ймовірність моделі можливо використовувати як обернені витрати).
Зворотне поширення (англ. backpropagation) — це метод, який використовують для підлаштовування ваг з'єднань для компенсування кожної помилки, виявленої під час навчання. Величина помилки фактично розподіляється між з'єднаннями. Технічно зворотне поширення обчислює градієнт (похідну) функції витрат, пов'язаний із заданим станом, відносно ваг. Уточнювання ваг можливо здійснювати за допомогою стохастичного градієнтного спуску (англ. stochastic gradient descent) або інших методів, таких як машини екстремального навчання,[107] «безпоширні» (англ. "no-prop") мережі,[108] тренування без вертання,[109] «безвагові» (англ. "weightless") мережі,[110][111] та не-конективістські нейронні мережі.
Кероване навчання (англ. supervised learning) використовує набір пар входів і бажаних виходів. Завдання навчання полягає в тому, щоби для кожного входу видавати бажаний вихід. У цьому випадку функція витрат пов'язана з усуненням неправильного висновування.[120] Витрати, які використовують зазвичай, це середньоквадратична похибка, яка намагається мінімізувати середню квадратичну похибку виходу мережі відносно бажаного виходу. Для керованого навчання підходять завдання на розпізнавання образів (також відоме як класифікування) та регресію (також відоме як наближення функції). Кероване навчання також застосовне до послідовних даних (наприклад, для розпізнавання рукописного тексту, мовлення та жестів[en]). Його можливо розглядати як навчання з «учителем» у вигляді функції, яка забезпечує безперервний зворотний зв'язок щодо якості отриманих на даний момент рішень.
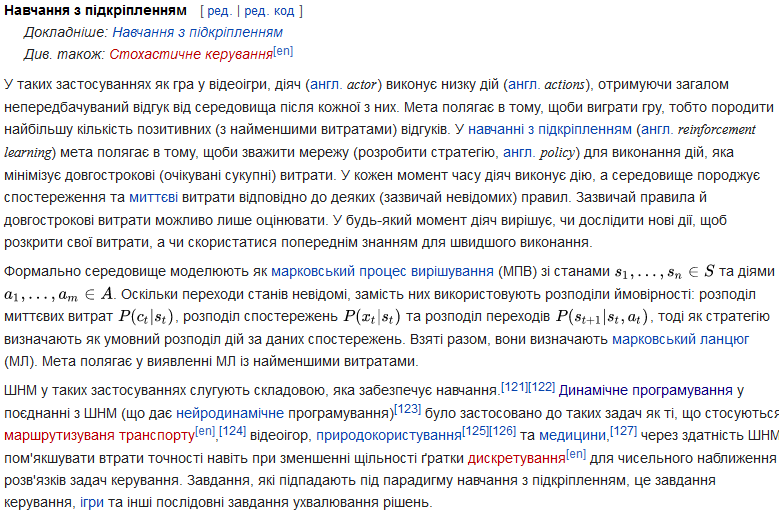
Самонавчання (англ. self-learning) в нейронних мережах було запропоновано 1982 року разом із нейронною мережею, здатною до самонавчання, названою поперечинним адаптивним масивом (ПАМ, англ. crossbar adaptive array, CAA).[128] Це система лише з одним входом, ситуацією s, й лише одним виходом, дією (або поведінкою) a. Вона не має ані входу зовнішніх порад, ані входу зовнішнього підкріплення з боку середовища. ПАМ обчислює поперечним чином як рішення щодо дій, так і емоції (почуття) щодо виниклих ситуацій. Ця система керується взаємодією між пізнанням та емоціями.[129] За заданої матриці пам'яті, W =||w(a, s)||, поперечинний алгоритм самонавчання на кожній ітерації виконує наступне обчислення:
У ситуації s виконати дію a;
Отримати наслідкову ситуацію s';
Обчислити емоцію перебування в наслідковій ситуації v(s');
Уточнити поперечинну пам'ять w'(a,s) = w(a,s) + v(s').
Поширюване зворотно значення (вторинне підкріплення, англ. secondary reinforcement) — це емоція щодо наслідків ситуації. ПАМ існує у двох середовищах: одне — поведінкове середовище, де вона поводиться, а інше — генетичне середовище, де вона спочатку й лише один раз отримує початкові емоції щодо ситуацій, з якими можливо зіткнутися в поведінковому середовищі. Отримавши геномний вектор (видовий вектор, англ. genome vector, species vector) із генетичного середовища, ПАМ навчатиметься цілеспрямованої поведінки в поведінковому середовищі, що містить як бажані, так і небажані ситуації.
Нейроеволюція (англ. neuroevolution) може створювати топології та ваги нейронної мережі за допомогою еволюційного обчислення. Завдяки сучасним вдосконаленням нейроеволюція конкурує зі складними підходами градієнтного спуску.[131] Одна з переваг нейроеволюції полягає в тому, що вона може бути менш схильною потрапляти в «глухий кут».[132]
Стохастичні нейронні мережі (англ. stochastic neural networks), що походять від моделей Шеррінгтона — Кіркпатріка[en], це один з типів штучних нейронних мереж, побудований шляхом введення випадкових варіацій у мережу, або надаванням штучним нейронам мережі стохастичних передавальних функцій, або надаванням їм стохастичних ваг. Це робить їх корисними інструментами для розв'язування задач оптимізації, оскільки випадкові флуктуації допомагають мережі уникати локальних мінімумів.[133] Стохастичні нейронні мережі, треновані за допомогою баєсового підходу, відомі як баєсові нейронні мережі (англ. Bayesian neural network).[134]
Інші. У баєсовій системі обирають розподіл над набором дозволених моделей таким чином, щоби мінімізувати витрати. Іншими алгоритмами навчання є еволюційні методи,[135] генно-експресійне програмування[en],[136] імітування відпалювання,[137] очікування-максимізація, непараметричні методи[en] та метод рою частинок.[138] Збіжна рекурсія (англ. convergent recursion) — це алгоритм навчання для нейронних мереж артикуляційних контролерів мозочкової моделі[en] (АКММ, англ. cerebellar model articulation controller, CMAC).
Є два режими навчання: стохастичний (англ. stochastic) та пакетний (англ. batch). У стохастичному навчанні кожен вхід створює підлаштовування ваг. У пакетному навчанні ваги підлаштовують на основі пакету входів, накопичуючи похибки в пакеті. Стохастичне навчання вносить «шум» до процесу, використовуючи локальний градієнт, розрахований з однієї точки даних; це знижує шанс застрягання мережі в локальних мінімумах. Проте пакетне навчання зазвичай дає швидший і стабільніший спуск до локального мінімуму, оскільки кожне уточнення виконується в напрямку усередненої похибки пакета. Поширеним компромісом є використання «мініпакетів» (англ. "mini-batches"), невеликих пакетів зі зразками в кожному пакеті, обраними стохастично з усього набору даних.
Побудова мереж. Пошук нейронної архітектури (ПНА, англ. neural architecture search, NAS) використовує машинне навчання для автоматизування побудови ШНМ. Різні підходи до ПНА побудували мережі, добре порівнянні з системами, розробленими вручну. Основним алгоритмом цього пошуку є пропонувати модель-кандидатку, оцінювати її за набором даних, і використовувати результати як зворотний зв'язок для навчання мережі ПНА.[150] Серед доступних систем — АвтоМН та AutoKeras.[151]
До проблем побудови належать визначення кількості, типу та з'єднаності рівнів мережі, а також розміру кожного, та типу з'єднання (повне, агрегувальне, …).
Гіперпараметри також слід визначати як частину побудови (їх не навчаються), керуючи такими питаннями як кількість нейронів у кожному шарі, темп навчання, крок, крок фільтрів (англ. stride), глибина, рецептивне поле та доповнення (для ЗНМ) тощо.[152]
Використання штучних нейронних мереж вимагає розуміння їхніх характеристик.
Вибір моделі: Це залежить від подання даних та застосування. Надмірно складні моделі навчаються повільно.
Алгоритм навчання: Існують численні компроміси між алгоритмами навчання. Майже кожен алгоритм працюватиме добре з правильними гіперпараметрами[153] для тренування на певному наборі даних. Проте обрання та налаштування алгоритму для навчання на небачених даних вимагає значного експериментування.
Робастність: Якщо модель, функцію витрат та алгоритм навчання обрано належним чином, то отримана ШНМ може стати робастною.
Можливості ШНМ підпадають під наступні широкі категорії:
Наближування функцій[en],[155] або регресійний аналіз,[156] включно з передбачуванням часових рядів, наближуванням допасованості[en][157] та моделюванням.
Класифікування, включно з розпізнаванням образів та послідовностей, виявлянням новизни[en] та послідовним ухвалюванням рішень.[158]
Обробка даних,[159] включно з фільтруванням, кластеруванням, сліпим виокремлюванням сигналу[en][160] та стисканням.
Робототехніка, включно зі скеровуванням маніпуляторів та протезів.
Застосування. Завдяки своїй здатності відтворювати та моделювати нелінійні процеси штучні нейронні мережі знайшли застосування в багатьох дисциплінах. До сфер застосування належать ідентифікування систем[en] та керування ними (керування транспортними засобами, передбачування траєкторії,[161] керування процесами, природокористування), квантова хімія,[162] універсальна гра в ігри[en],[163] розпізнавання образів (радарні системи, встановлювання облич, класифікування сигналів,[164] тривимірна відбудова,[165] розпізнавання об'єктів тощо), аналіз даних давачів,[166] розпізнавання послідовностей (розпізнавання жестів, мовлення, рукописного та друкованого тексту[167]), медична діагностика, фінанси[168] (наприклад, передподійні[en] моделі для окремих фінансових довготривалих прогнозів та штучні фінансові ринки[en]), добування даних, унаочнювання, машинний переклад, соціальномережне фільтрування[169] та фільтрування спаму електронної пошти[en]. ШНМ використовували для діагностування кількох типів раку[170][171] та для відрізнювання високоінвазивних ліній ракових клітин від менш інвазивних з використанням лише інформації про форму клітин.
ШНМ використовували для прискорювання аналізу надійності інфраструктури, що піддається стихійним лихам,[174][175] і для прогнозування просідання фундаментів.[176] Також може бути корисним пом'якшувати повені шляхом використання ШНМ для моделювання дощового стоку.[177] ШНМ також використовували для побудови чорноскринькових моделей в геонауках: гідрології,[178][179] моделюванні океану та прибережній інженерії[en],[180][181] та геоморфології.[182] ШНМ використовують у кібербезпеці з метою розмежовування законної діяльності від зловмисної. Наприклад, машинне навчання використовували для класифікування зловмисного програмного забезпечення під Android,[183] для визначання доменів, що належать суб'єктам загрози, і для виявляння URL-адрес, які становлять загрозу безпеці.[184] Ведуться дослідження систем ШНМ, призначених для випробування на проникнення, для виявляння бот-мереж,[185] шахрайства з кредитними картками[186] та мережних вторгнень.
ШНМ пропонували як інструмент для розв'язування частинних диференціальних рівнянь у фізиці[187][188][189] та моделювання властивостей багаточастинкових відкритих квантових систем[en].[190][191][192][193] У дослідженні мозку ШНМ вивчали короткочасну поведінку окремих нейронів,[194] динаміку нейронних ланцюгів, що виникає через взаємодію між окремими нейронами, та те, як поведінка може виникати з абстрактних нейронних модулів, які подають цілі підсистеми. Дослідження розглядали довгострокову та короткочасну пластичність нейронних систем та їхній зв'язок із навчанням і пам'яттю від окремого нейрона до системного рівня.
Функція активації, або передавальна функція (англ. activation function[1][2][3][4][5], також excitation function, squashing function, transfer function[6]) штучного нейрона — залежність вихідного сигналу штучного нейрона від вхідного.
Зазвичай передавальна функція ϕ(x) відображає дійсні числа на інтервал (−1,1) або (0,1).
Більшість видів нейронних мереж для функції активації використовують сигмоїди[2]. ADALINE і самоорганізаційні карти використовують лінійні функції активації, а радіально базисні мережі використовують радіальні базисні функції[1].
Математично доведено, що тришаровий перцептрон з використанням сигмоїдної функції активації може апроксимувати будь-яку неперервну функцію з довільною точністю (Теорема Цибенка)[1].
Метод зворотного поширення помилки вимагає, щоб функція активації була неперервною, нелінійною, монотонно зростаючою, і диференційовною[1].
В задачі багатокласової[en] класифікації нейрони останнього шару зазвичай використовують softmax як функцію активації[3].
У хемометриці — функція, яка використовується в методі нейронної сітки для перетворення у вузлах вхідних даних з будь-якої області значень (зокрема неперервних) у чітко окреслений ряд значень (напр., в 0 чи 1).[7]
Порівняння передавальних функцій. Деякі бажані властивості передавальної функції включають:
Нелінійна — коли передавальна функція нелінійна, то, як доведено, двошарова нейронна мережа є універсальною апроксимацією функцій.[8] Тотожна передавальна функція не має такої властивості. Коли декілька шарів використовують тотожну передавальну функцію, тоді вся мережа еквівалентна одношаровій моделі.
Неперервна диференційовність — ця властивість бажана (RELU не є неперервно диференційовною і має неоднозначне рішення для оптимізації заснованій на градієнті) для використання методів оптимізації заснованих на градієнті. Передавальна функція двійковий крок не диференційовна у 0, але диференційовна в усіх інших значення, що є проблемою для методів заснованих на градієнті.[9]
Область визначення.
Монотонність.
Гладка функція з монотонною похідною.
Наближення до тотожної функції f ( x ) = x {\displaystyle f(x)=x} в початку координат.
Гаусовая функція:
Апроксимація. Радіальні базисні функції зазвичай використовуються для побудови апроксимації функцій[en] у вигляді
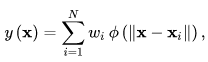
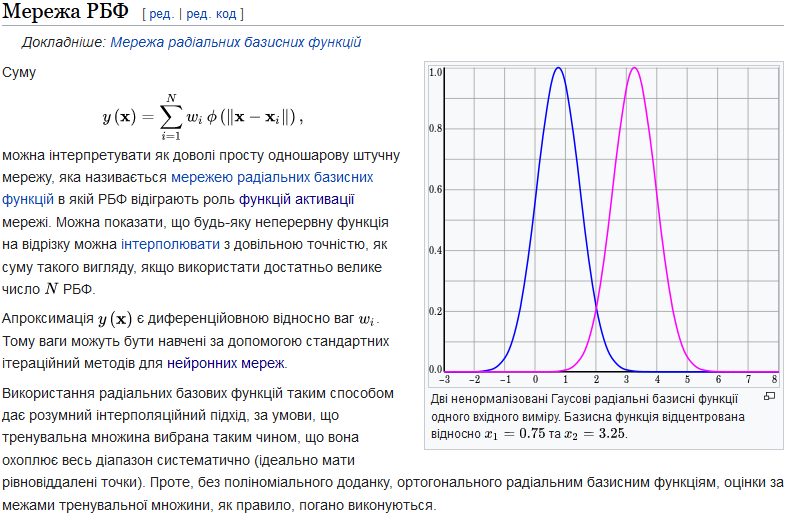
Як працюють нейрони. Нейронна мережа структурно та функціонально повторює роботу нервової системи живих організмів. Вона складається з безлічі штучних нейронів, які пов'язані у вигляді сіток та шарів. Взаємодіючи один з одним, вони передають дані від сітки до сітки та від шару до шару. Завдяки цьому нейронки можуть виконувати складні завдання: наприклад, розпізнавати картинки чи прогнозувати.
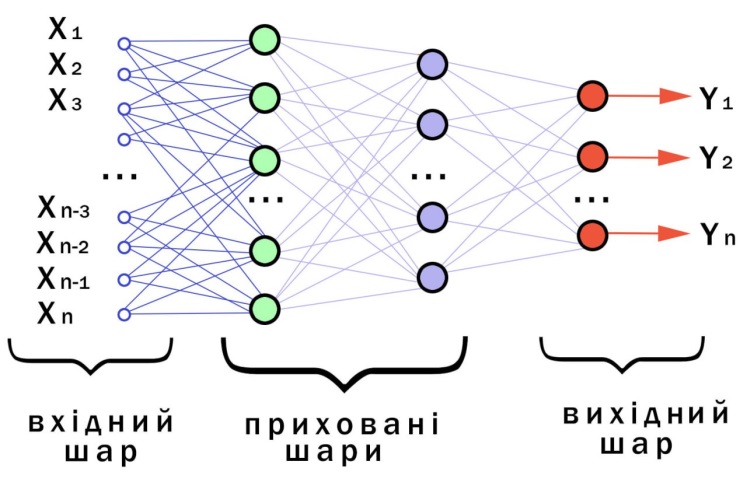
Найпростіша схема нейронної мережі
Базовий блок будь-якої нейронної мережі — це нейрон. Він працює за таким принципом:
1. Штучний нейрон отримує вхідні значення xi , які можуть виглядати як векторні або числові значення, що представляють ознаки або значення попередніх нейронів.
2. Вхідне значення множиться на відповідну вагу. Ця вага (wji) визначає важливість цього входу для обчислень нейрона. Отримані в результаті множення значення підсумовуються:
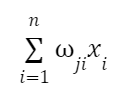
3. До суми зважених значень додається зміщення. Зміщення (bias) у штучному нейроні — це додатковий параметр, деяке константне значення, завдяки якому нейрон може активуватися, навіть якщо зважені входи набувають нульового значення.
Важливо! Без зміщення нейронна мережа могла б представляти лише лінійні відображення, а це обмежило б її здатність розв'язувати складні завдання та витягувати складні патерни з даних.
4. Отримана сума передається через функцію активації, яка застосовує нелінійне перетворення до виваженої суми. Функція активації визначає вихідний сигнал нейрона, додаючи нелінійності до моделі.
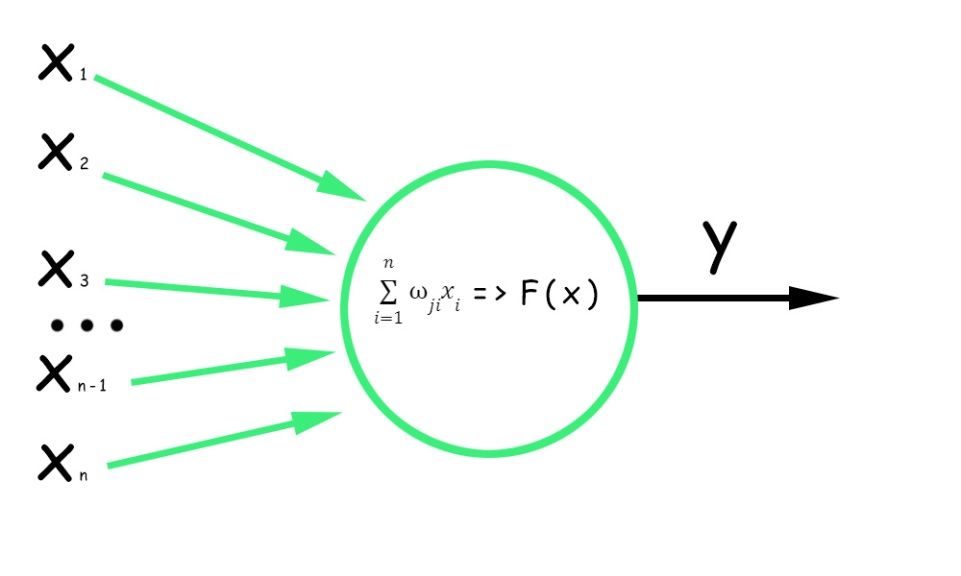
Як працює нейрон
Зверніть увагу, що й усунення, і функція активації разом впливають на активацію нейрона. Зміщення дозволяє встановити базовий рівень активації, тоді як функція активації визначає, як змінюватиметься активація нейрона залежно від входів та зсуву. У прихованих шарах нейронної мережі зазвичай (не завжди, але найчастіше) використовується та сама функція активації нейронів. Для вихідного шару функція активації трохи змінюється.
Порогова (ступінчаста) функція
Найпростіша функція активації. Іноді її називають функцією Гевісайда. Якщо значення ступінчастої функції перевищує певний поріг, нейрон вважається активованим:
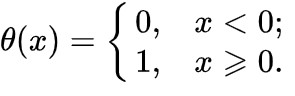
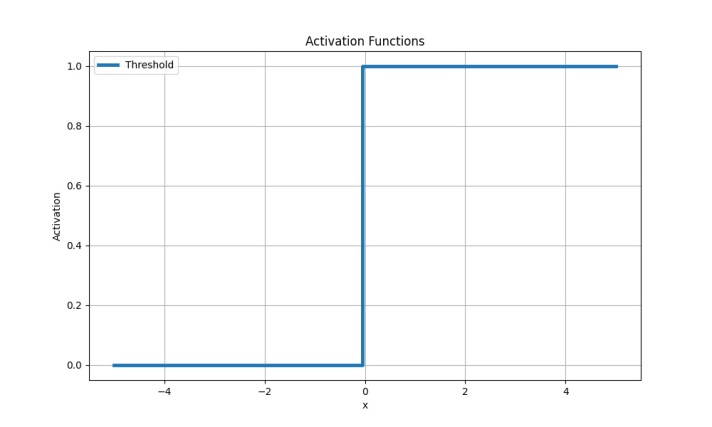
Порогова (ступінчаста) функція активації
Недоліки
Порогова функція безперервна і недиференційована, внаслідок чого ми отримуємо дві проблеми, через які в нейромережах із глибоким навчанням ця функція майже не використовується:
1. Перша проблема пов'язана з алгоритмом зворотного поширення помилки Backpropagation — механізмом навчання нейронної мережі. Завдяки йому налаштовуються ваги зв'язків між нейронами мережі з урахуванням обчислених помилок прогнозування.
Обчислити градієнт, необхідний для оновлення ваг у процесі навчання мережі, можна лише з функціями активації, що диференціюються (градієнт обчислюється за допомогою похідної функції активації з входу нейрона).
2. Друга проблема — стрибки у функції активації Гевісайда. Вони призводять до безперервних змін вихідних значень нейронів за невеликих змін вхідних даних. В результаті мережа може «застрягати» у певних ділянках нейронної мережі, де вихідні значення нейронів стрибають між двома різними значеннями.
Таке застрягання ускладнює відновлення ваг нейронів у цих регіонах, оскільки невеликі зміни ваг не призводять до безперервних змін виходів нейронів. В результаті мережа може не зміститися в потрібному напрямку та не досягти оптимальних значень ваг.
Лінійна функція
Ще одна найпростіша функція активації, в якій зміни вхідного сигналу пропорційно впливають на вихід без будь-яких нелінійних перетворень:
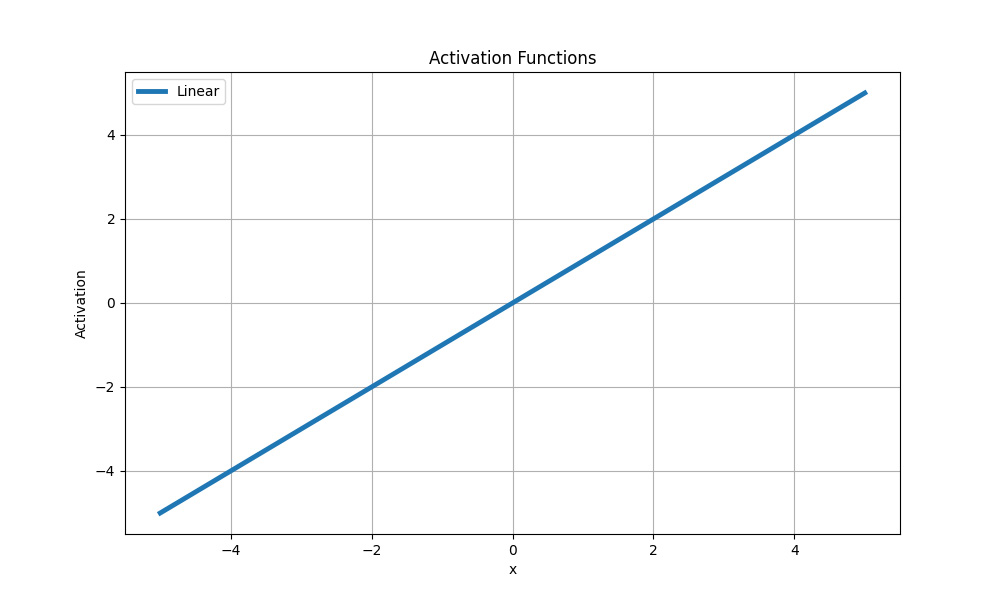
Лінійна функція активації
У зв'язку з цим застосування лінійної функції обмежене завданнями регресії, де потрібне передбачення безперервного значення. Наприклад, у задачі передбачення ціни на нерухомість з урахуванням різних ознак вона може бути застосована до вихідного шару.
Також функція може бути застосована до окремих лінійних шарів мережі, які виконують лінійні операції над входами. У цьому випадку функція активації легко передає значення без нелінійних перетворень.
Приклад використання
Припустімо, ми розв'язуємо завдання прогнозування продажу товарів на основі їхніх рекламних витрат.
Дано:
відомості про суму грошей, витрачених на рекламу у різних медіаканалах (розкрутка на телебаченні/радіо, у соціальних мережах);
відповідні відомостям обсяги продажу товарів.
Кінцева мета цієї задачі — побудова моделі, яка прогнозувала б обсяг продажів на основі вхідних даних.
Задіємо нейронну мережу з одним лінійним шаром та лінійною функцією активації. Вхідними даними будуть значення рекламних витрат у різних каналах, а вихідними даними — прогнозований обсяг продажу.
Нейронна мережа з лінійною функцією активації дозволить встановити лінійну залежність між рекламними витратами та обсягом продажу. Модель прагнутиме знайти оптимальні ваги для кожного каналу реклами, щоб якнайкраще передбачати обсяг продажів на основі даних про витрати.
Недоліки
Лінійна функція активації придатна тільки для простих моделей або як заключний шар у нейронній мережі для розв'язання задач регресії, де потрібно виконати прогнозування числового значення.
Сигмоїдна функція (логістична)
Логістична функція нелінійна та стискає вхідні значення від 0 до 1 за формулою:
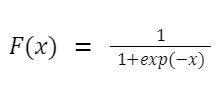
де x — вхідне значення.
Найчастіше сигмоїдна функція активації застосовується у задачах бінарної класифікації, де потрібно передбачити можливість приналежності до одного з двох класів. Вона конвертує вхідні значення у ймовірності, які можуть бути інтерпретовані як імовірність приналежності до позитивного класу.
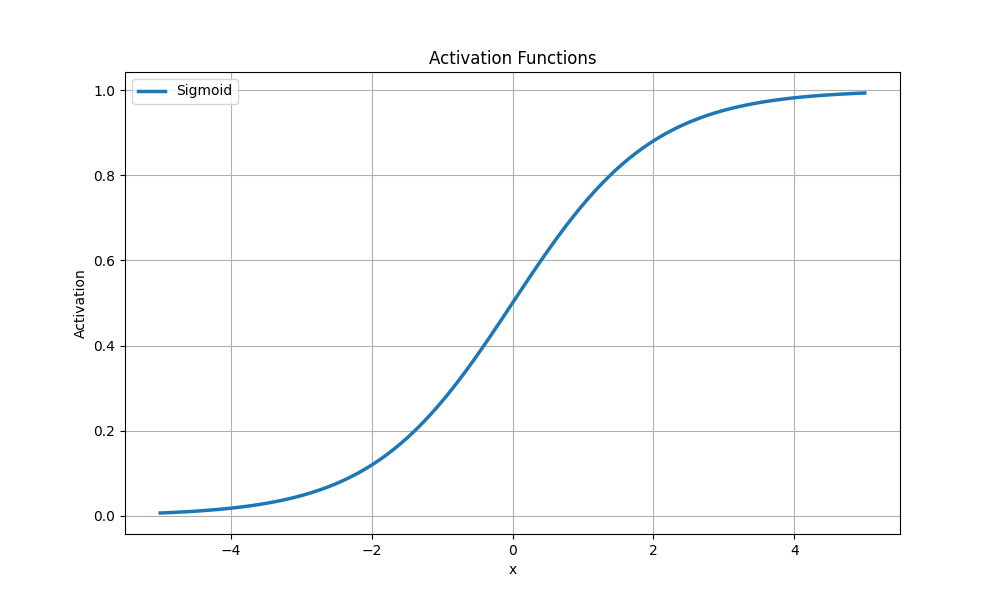
Сигмоїдна функція активації
Функція активації визначає вихідний сигнал нейрона з урахуванням його входу. Ми просто підставляємо до неї підсумоване значення добутку нейронних вхідних сигналів та коефіцієнтів ваг — і отримуємо вихідний сигнал нейронної мережі.
Нижче вказані переваги та недоліки різних функцій активації:
Порогова функція бінарна та використовується рідко через свою безперервність і відсутність градієнта.
Лінійна функція активації передає вхідний сигнал без змін, тому застосовується у простих моделях і не підходить для представлення складних нелінійних залежностей.
Гіперболічний тангенс (tanh) стискає вхідні значення в діапазоні від -1 до 1. Він часто використовується вприхованих шарах нейронних мереж зберігаючи негативні значення та забезпечуючи нелінійність.
Сигмоїда перетворює вхідні значення в діапазоні від нуля до одиниці. Вона часто використовується в задачах класифікації, але страждає від проблеми градієнта, що згасає, під час навчання глибоких нейронних мереж.