10.2. Пошук у просторі станів та подання знань
10.2.1. Стратегії пошуку в просторі станів: пошук в ширину, пошук в глибину, двонаправлений пошук.
Пошук рішень інтелектуальних задач у просторі станів
У більшості СШІ інформація, доступна стратегія керування недостатня для того, щоб вибрати відповідне правило на кожному кроці процесу. Тому самі процедури виведення є, як правило, пошуковими процедурами. Оскільки поняттям знання про завдання можуть відповідати стани завдання, а правилам виведення – оператори переходу з одного стану в інший від завдання до підзадач, то процедура пошуку рішення називається пошуком у просторі станів. Пошук рішень у просторі станів зводиться до визначення послідовності операторів, які відображають початкові стани в цільові. Причому якщо така послідовність не одна й задано критерій оптимальності, то пошук зводиться до визначення оптимальної послідовності операторів, які забезпечують оптимум заданого критерію оптимальності.
Методи пошуку рішень у просторі станів зручно розглянути, використовуючи дерево (граф) станів. На дереві станів (рис. 2.1) пошук рішення зводиться до визначення шляху (оптимального, якщо задано критерій оптимальності) від кореня дерева до цільової вершини А, тобто до вершини, яка відповідає цільовому стану. Вершини В і С є вершинами, що розкриваються (обчислюваними, проміжними). Вершина D термінальна, тобто завершальна. Ребра, що з’єднують вершини, означають приєднані процедури, які необхідно виконати, щоб перейти до наступного стану (вершини). Процес застосування приєднаних процедур називають породженням вершин або перебором варіантів. При породженні нової вершини обов’язково запам’ятовується покажчик на стару. У кінці перебору сукупність цих покажчиків утворює шлях вирішення задачі, який записується разом із іменами виконаних приєднаних процедур. Для знаходження рішення необхідно знову і знову вибирати, перевіряти й розкривати вузли доти, поки не буде знайдено розв’язок або не залишиться більше станів, які можна було б розгорнути. Порядок, у якому відбувається розгортання станів, визначається стратегією пошуку.
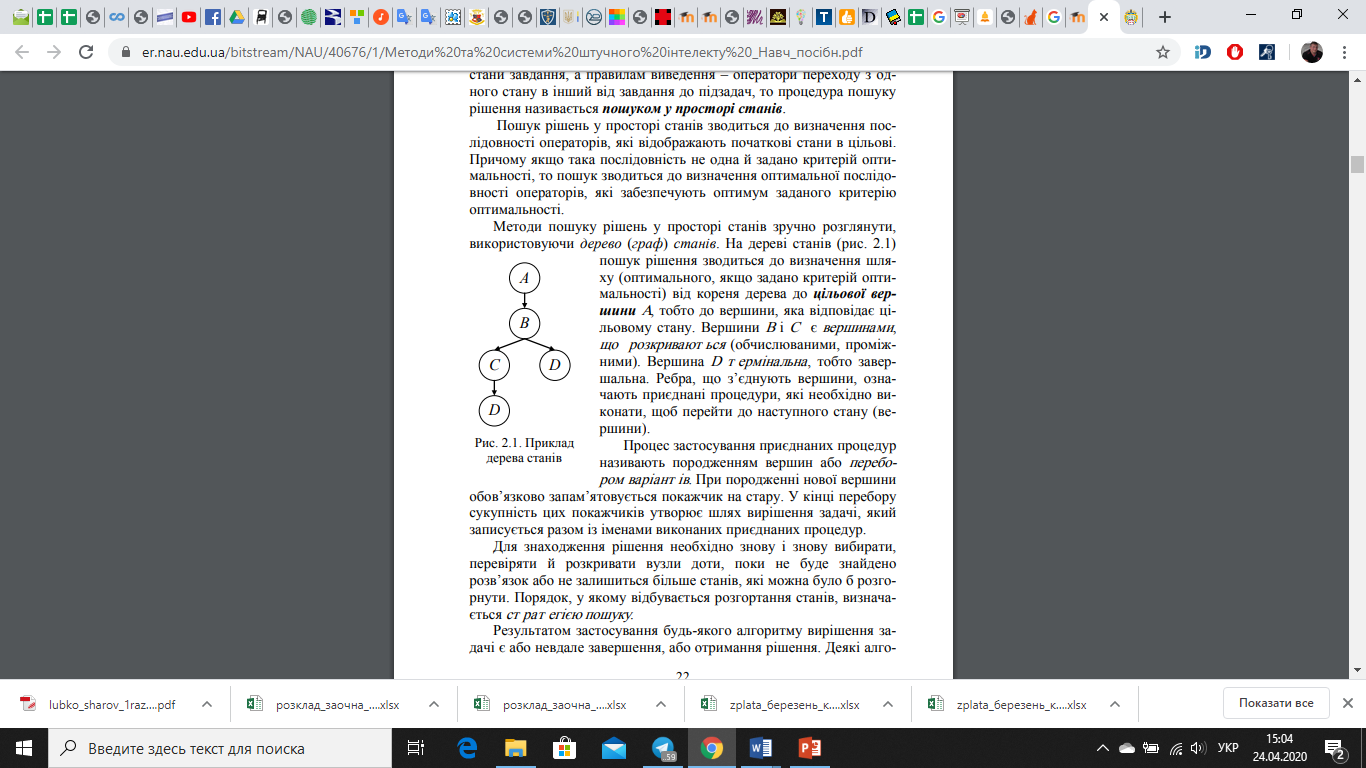
Рис. 2.1. Приклад дерева станів
Методи пошуку в одному просторі призначені для використання за таких умов: області невеликої розмірності, повнота моделі, точні та повні дані. Стратегії пошуку в одному просторі можна класифікувати так:
1. Неінформований пошук («сліпі» методи): − в ширину; − в глибину (з обмеженням глибини, з ітеративним поглибленням).
2. Інформований пошук (евристичний пошук). Пошук може здійснюватись у різних напрямках.
Прямий пошук йде від вихідного стану і, як правило, використовується тоді, коли цільовий стан задано неявно.
Зворотний пошук йде від цільового стану і використовується тоді, коли початковий стан задано неявно, а цільовий ‒ явно.
Двонаправлений метод пошуку дозволяє одночасно проводити два пошуки в прямому і у зворотному напрямку, зупиняючись після того, як два процеси пошуку зустрінуться на середині. У такому разі передбачається перевірка в одному або в обох процесах пошуку кожного вузла перед його розгортанням для визначення того, чи не знаходиться він на периферії іншого дерева пошуку. Уразі позитивного результату перевірки рішення знайдено і пошук припиняється.
Методи неінформованого або «сліпого» пошуку (повного перебору) означають, що в даних стратегіях не використовується додаткова інформація про стани, крім тієї, яка подана у завданні. Такі стратегії можуть лише виробляти наступників і відрізняти цільовий стан від нецільового. Потребують великої витрати часу. Пошук у ширину є досить простою стратегією, в якій спочатку розгортається кореневий вузол, потім – усі його наступники (рис. 2.2).
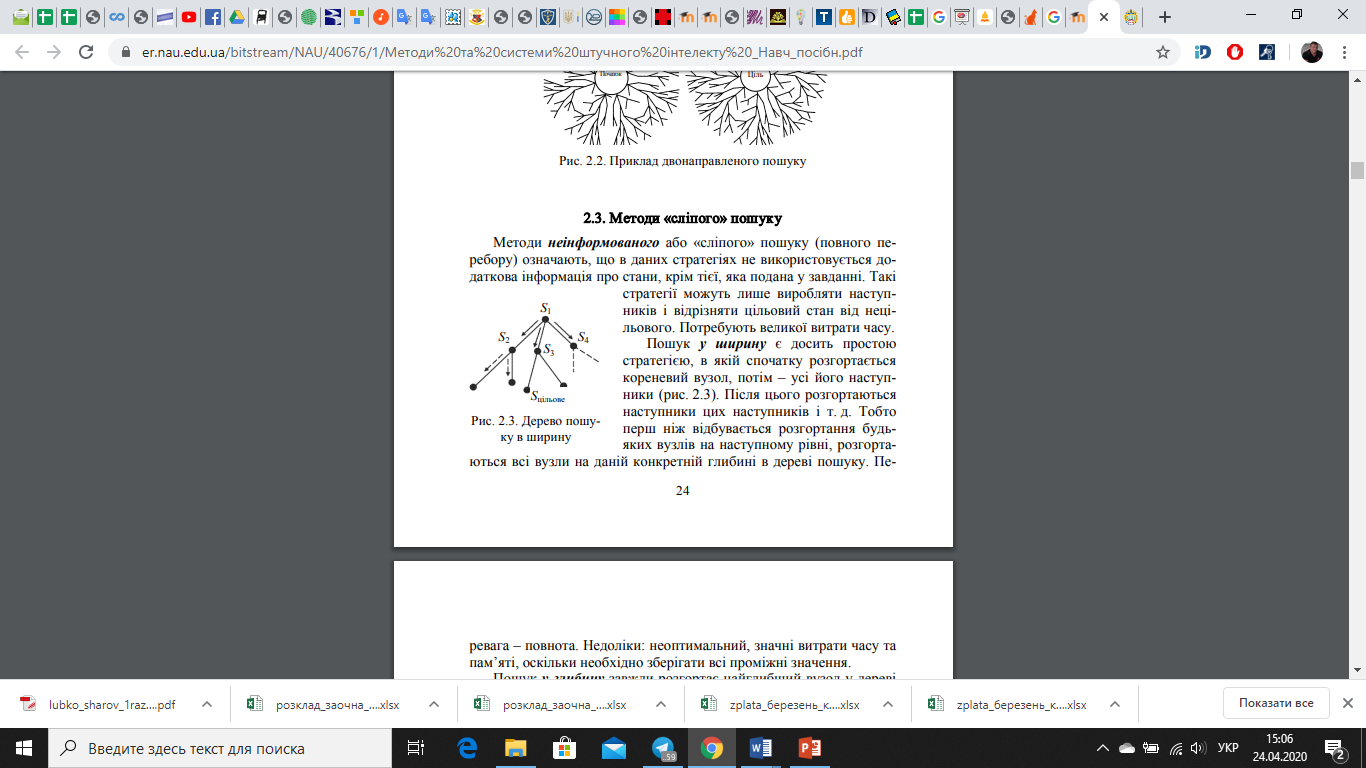
Рис. 2.2. Дерево пошуку в ширину
Після цього розгортаються наступники цих наступників і т. д. Тобто перш ніж відбувається розгортання будь-яких вузлів на наступному рівні, розгортаються всі вузли на даній конкретній глибині в дереві пошуку.
Перевага – повнота. Недоліки: неоптимальний, значні витрати часу та пам’яті, оскільки необхідно зберігати всі проміжні значення. Пошук у глибину завжди розгортає найглибший вузол у дереві пошуку (рис. 2.3). Пошук безпосередньо переходить на найглибший рівень дерева пошуку, на якому вузли не мають наступників.
У міру того, як ці вузли розгортаються, вони видаляються з периферії, тому надалі пошук «відновлюється» з наступного поверхневого вузла, який все ще має недосліджених наступників. Перевага – незначні потреби в пам’яті (зберігання лише єдиного шляху від кореня до листового вузла). Недолік – неоптимальний, може бути зроблений неправильний вибір і перехід у тупикову ситуацію, пов’язану з проходженням вниз по дуже довгому (чи навіть нескінченному) шляху, при тому, що інший варіант міг би привести до рішення, яке знаходиться недалеко від кореня дерева пошуку.
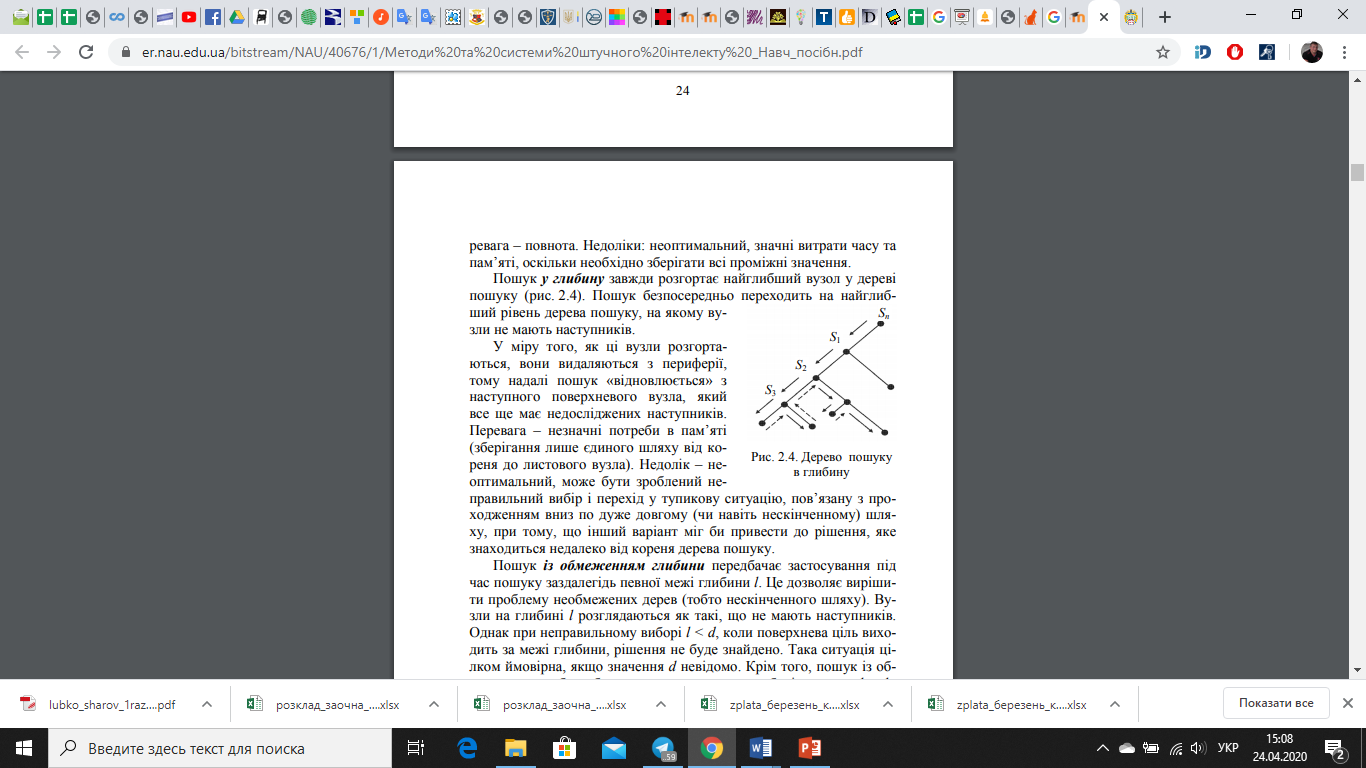
Рис. 2.3. Дерево пошуку в глибину
Пошук із обмеженням глибини передбачає застосування під час пошуку заздалегідь певної межі глибини l. Це дозволяє вирішити проблему необмежених дерев (тобто нескінченного шляху). Вузли на глибині l розглядаються як такі, що не мають наступників. Однак при неправильному виборі l < d, коли поверхнева ціль виходить за межі глибини, рішення не буде знайдено. Така ситуація цілком ймовірна, якщо значення d невідомо. Крім того, пошук із обмеженням глибини буде неоптимальним при виборі значення l > d.
Пошук углибину з ітеративним поглибленням передбачає поступове збільшення глибини пошуку (яка спочатку дорівнює 1, потім 2, 3 і т. д.) доти, поки не буде знайдено ціль. Така подія відбувається після того, як межа глибини досягає значення d, глибини поверхневого цільового вузла.
Методи повного перебору гарантують вирішення задачі, якщо воно існує, а за наявності декількох рішень гарантує оптимальне. Однак на практиці ці методи використовуються для вирішення лише невеликих за розмірами графів станів.
Для реальних випадків найчастіше використовується додаткова інформація, заснована на попередньому досвіді або отримана на підставі теоретичних висновків. Така інформація називається евристичною, а організована в правила – евристичними методами пошуку або евристиками. Евристична інформація має суто спеціальний характер і може застосовуватися лише в рамках даного завдання, в кращому випадку в рамках завдань даного класу, вона робить перебір впорядкованим.
У алгоритмах евристичного пошуку список відкритих вершин впорядковується за зростанням деякої оціночної функції, що формується на основі евристичних правил. Оціночна функція може включати дві складові, одна з яких називається евристичною і характеризує близькість поточної та цільової вершин. Що менше значення евристичної складової оціночної функції, то ближче розглянута вершина до цільової вершини. Евристичні методи найчастіше застосовуються не для пошуку єдино правильного (оптимального рішення), а для пошуку першого рішення, що задовольняє деякому критерію за певних обмежень.
Пошук у ширину — алгоритм пошуку на графі[1]. Якщо задано граф G = (V, E) та початкову вершину s, алгоритм пошуку в ширину систематично обходить всі досяжні із s вершини. На першому кроці вершина s позначається, як пройдена, а в список додаються всі вершини, досяжні з s без відвідування проміжних вершин. На кожному наступному кроці всі поточні вершини списку відмічаються, як пройдені, а новий список формується із вершин, котрі є ще не пройденими сусідами поточних вершин списку. Для реалізації списку вершин найчастіше використовується черга та принцип FIFO. Виконання алгоритму продовжується до досягнення шуканої вершини або до того часу, коли на певному кроці в список не включається жодна вершина. Другий випадок означає, що всі вершини, доступні з початкової, уже відмічені, як пройдені, а шлях до цільової вершини не знайдений.
Алгоритм має назву пошуку в ширину, оскільки «фронт» пошуку (між пройденими та непройденими вершинами) одноманітно розширюється вздовж всієї своєї ширини. Тобто, алгоритм проходить всі вершини на відстані k перед тим як пройти вершини на відстані k+1.[1]
Наведемо кроки алгоритму:
Почати з довільної вершини v. Виконати BFS(v):=1. Включити вершину v у чергу.
Розглянути вершину, яка перебуває на початку черги; нехай це буде вершина х. Якщо для всіх вершин, суміжних із вершиною х, уже визначено BFS-номери, то перейти до кроку 4, інакше - до кроку 3.
Нехай {x,y} - ребро, у якому номер BFS(у) не визначено. Позначити це ребро потовщеною суцільною лінією, визначити BFS(у) як черговий BFS-номер, включити вершину у чергу й перейти до кроку 2.
Виключити вершину х із черги. Якщо черга порожня, то зупинитись, інакше - перейти до кроку 2.
Просторова складність. Так як в пам'яті зберігаються всі розгорнуті вузли, просторова складність алгоритму становить O ( | V | + | E | ) {\displaystyle O(\vert V\vert +\vert E\vert )}.
Алгоритм пошуку з ітеративним поглибленням схожий на пошук в ширину тим, що при кожній ітерації перед переходом на наступний рівень досліджується повний рівень нових вузлів, але вимагає значно менше пам'яті.
Часова складність. Так як в гіршому випадку алгоритм відвідує всі вузли графу, при зберіганні графу у вигляді списків суміжності[en], тимчасова складність алгоритму становить O ( | V | + | E | ) {\displaystyle O(\vert V\vert +\vert E\vert )}.
Повнота. Якщо у кожного вузла є кінцеве число наступників, алгоритм є повним: якщо рішення існує, алгоритм пошуку в ширину його знаходить, незалежно від того, чи є граф кінцевим. Однак якщо рішення не існує, на нескінченному графі пошук не закінчується.
Оптимальність. Якщо довжини ребер графу рівні між собою, пошук в ширину є оптимальним, тобто завжди знаходить найкоротший шлях. В разі зваженого графу пошук в ширину знаходить шлях, що містить мінімальну кількість ребер, але не обов'язково найкоротший.
Пошук за критерієм вартості є узагальненням пошуку в ширину і оптимальний на зваженому графі з невід'ємними вагами ребер. Алгоритм відвідує вузли графу в порядку зростання вартості шляху з початкового вузла і зазвичай використовує чергу з пріоритетами.
Алгоритм пошуку в глибину (англ. Depth-first search, DFS) — алгоритм для обходу дерева, структури подібної до дерева, або графу. Робота алгоритму починається з кореня дерева (або іншої обраної вершини в графі) і здійснюється обхід в максимально можливу глибину до переходу на наступну вершину.[1]
Нехай G=(V, E) — простий зв'язний граф, усі вершини якого позначено попарно різними символами. У процесі пошуку вглиб вершинами графу G надають номери (DFS-номери) та певним способом даних для збереження множин, яку називають стеком. Зі стеку можна вилучити тільки той елемент, котрий було додано до нього останнім: стек працює за принципом «останній прийшов — перший вийшов» (LIFO). Інакше кажучи, додавання й вилучення елементів у стеку відбувається з одного кінця, який називається верхівкою стеку. DFS-номери вершини х позначають DFS(х).
Наведемо кроки алгоритму:
Почати з довільної вершини v. Виконати DFS(v):=1. Включити цю вершину в стек.
Розглянути вершину у верхівці стеку: нехай це вершина х. Якщо всі ребра, інцидентні вершині х, позначено, то перейти до кроку 4, інакше — до кроку 3.
Нехай {x, y} — непозначене ребро. Якщо DFS(у) уже визначено, то позначити ребро {x, y} штриховою лінією та перейти до кроку 2. Якщо DFS(у) не визначено, то позначити ребро {x, y} потовщеною суцільною лінією, визначити DFS(у) як черговий DFS-номер, включити цю вершину в стек і перейти до кроку 2.
Виключити вершину х зі стеку. Якщо стек порожній, то зупинитись, інакше — перейти до кроку 2.
Обчислювальною складністю алгоритму (або просто складністю) назвемо кількість кроків виконуваних алгоритмом в гіршому випадку. Вона є функцією від розмірності задачі, представленої вхідними даними. Наприклад, для графу, що задається списками інцидентності, розмірність задачі представляється як пара (n, m). Складність алгоритму визначається, як функція f, така, що f (n, m) дорівнює числу кроків алгоритму для довільного графу з n вершинами і m ребрами. Під кроком алгоритму розуміється машинна команда, і при такому визначенні кроку обчислювальна складність залежить від конкретної системи команд і способу трансляції. Нас же буде надалі цікавити не точна складність алгоритму, обчислення якої практично неможливо, а асимптотична складність, яка визначається швидкістю росту числа кроків алгоритму при необмеженому збільшенні розмірності задачі. Крім того, обчислювальна складність алгоритму, обчислена при різних системах команд або способах трансляції, відрізняються один від одного в p разів, де p — речова константа, а їх швидкість росту однакова. Для порівняння швидкості росту двох функцій f(n) i g(n) будемо використовувати позначення f(n) = O[g(n)] або f(n) = Ω[g(n)]. Будемо говорити, що функція f(n) має порядок зростання не більше, ніж функція g(n), що позначається f(n) = O[g(n)], тоді і тільки тоді, коли існують C = const і N > 0, такі, що |f(n)| <= C|g(n)| n>= N Будемо говорити, що функція f(n) має порядок зростання не менше, ніж функція g(n), що позначається f(n) = Ω[g(n)], тоді і тільки тоді, коли існують C = const і N > 0, такі, що |f(n)| >= C|g(n)| n>= N Оцінимо обчислювальну складність рекурсивного варіанту алгоритму пошуку у глибину. O(n) + O(2m) = O(n) + O(m) = O(n+m).
Двонаправлений пошук — ускладнений алгоритм пошуку ушир або пошуку углиб, в основі якого лежить така ідея, що можна одночасно проводити два пошуки (в прямому напрямку, від початкового стану, та у зворотному напрямку, від цілі), зупиняючись після того, як два процеси пошуку зустрінуться на середині.
Ідея. Нехай b — максимальний коефіцієнт розгалуження дерева пошуку та d — глибина оптимального розв'язку в дереві пошуку. Як показано на рис. 1, значення bd/2 + bd/2 набагато менше, ніж bd, або, як показано на малюнку, площа двох невеликих кіл менше площі одного великого кола з центром на початку пошуку, який охоплює ціль пошуку.
Двонаправлений пошук реалізується за допомогою методу, у якому передбачається перевірка в одному або обох процесах пошуку кожного вузла перед його розгортанням для визначення того, чи не знаходиться він на периферії іншого дерева пошуку; у випадку позитивного результату перевірки рішення знайдено. Наприклад, якщо задача має рішення на глибині d = 6 і в кожному напрямку здійснюється пошук ушир із послідовним розгортанням по одному вузлу, то у найгіршому випадку ці два процеси пошуку зустрінуться, якщо у кожному з них будуть розгорнуті усі вузли на глибині 3, крім одного. Це означає, що при b = 10 буде сформована загальна кількість вузлів, рівне 22 200, а не 11 111 100, як при стандартному пошуку ушир. Перевірка належності вузла до іншого дерева пошуку може бути виконана за сталий час за допомогою хеш-таблиці, тому часова складність двонаправленого пошуку визначається як O(bd/2). У пам'яті необхідно зберігати щонайменше одне з дерев пошуку, для того, щоб можна було виконати перевірку належності до іншого дерева, тому просторова складність також визначається як O(bd/2). Такі вимоги до простору є одним з найістотніших недоліків двонаправленого пошуку. Цей алгоритм є повним та оптимальним (при однакових вартостях етапів), якщо обидва процеси пошуку здійснюються ушир; інші сполучення методів можуть характеризуватися відсутністю повноти, оптимальності або того та іншого.
Принцип реалізації. Двонаправлений пошук стає привабливим завдяки зменшенню часової складності, але постає питання, як організувати пошук у зворотному напрямку. Це не так легко як здається на перший погляд. Припустимо, що попередниками вузла n, що визначаються за допомогою функції Pred(n), є всі ті вузли, для яких n слугує наступником. Для двонаправленого пошуку потрібно, щоб функція визначення попередника Pred(n) була ефективно обчислюваною. Напростішим є такий випадок, коли всі дії у просторі станів оборотні таким чином, що Pred(n) = Succ-1(n), а інші випадки можуть потребувати проявити значну винахідливість.
Розглянемо питання про те, що мається на увазі під поняттям «ціль» при пошуку «у зворотному напрямку від цілі». В задачі гри у вісім та пошуку маршруту на графі є тільки один цільовий стан, тому зворотний пошук дуже схожий на прямий пошук. Якщо ж є декілька явно перерахованих цільових станів, то може бути створений новий фіктивний цільовий стан, безпосередніми попередниками якого є всі фактичні цільові стани. Інакше, формуванню деяких надлишкових вузлів можна запобігти, розглядаючи множину цільових станів як єдиний цільовий стан, кожним з попередників якого є також множина станів, а саме, множина станів, що має відповідного наступника у множині цільових станів.
Найскладнішим випадком двонаправленого пошуку є така задача, в якій для перевірки цілі дається тільки неявний опис деякої (можливо, великої) множини цільових станів, наприклад всіх станів, що відповідають перевірці цілі «мат» у грі в шахи. При зворотному пошуку треба було б створити компактні описи «всіх станів, що дозволяють поставити мат за допомогою ходу m1» і т. д.; і ці описи треба було б звіряти зі станами, що формуються під час прямого пошуку. Загального способу ефективного рішення такої проблеми не існує.