2.1 Функції бінарної логіки
Алгебра логіки (Булева алгебра, Булева логіка, двійкова логіка, двійкова алгебра, англ. Boolean algebra) — розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями.[1] В алгебрі логіки значенням змінних є значення істинності істина або хиба, які зазвичай визначаються як 1 і 0 відповідно. На відміну від елементарної алгебри, у якій значеннями змінних є числа, а основними операціями є додавання і множення, основними операціями булевої алгебри є кон'юнкція операція І (англ. AND) позначається як ∧, диз'юнкція АБО (англ. OR) позначається як ∨, і заперечення НІ (англ. NOT) позначається як ¬. Таким чином, формалізм для описання логічних відношень є аналогічним тому, як описуються числові відношення в елементарній алгебрі.
Булеву алгебру запропонував Джордж Буль у своїй книзі Математичний аналіз логіки (1847), і більш детально в наступній книзі Дослідження законів думки[en] (1854). Відповідно до Гантінгтона[en], термін «Булева алгебра» вперше запропонував Шеффер у 1913, хоча Чарлз Сандерс Пірс у 1880 дав назву «Булева алгебра з однією сталою» першій главі своєї книги «Найпростіша математика». Булева алгебра є фундаментальною основою для розвитку цифрової електроніки, і втілена в усіх мовах програмування. Вона також використовується в теорії множин і статистиці.
2.2 Представлення даних на рівні машин
У системах автоматичного керування існує два потоки інформації: перший потік — це інформація про об'єкт керування, яка сприймається датчиками через канали, і засоби обробки і поступає у систему автоматичного керування; другий потік — це керівна інформація, яку видає комп'ютер системи автоматичного керування на виконавчі пристрої через засоби обробки інформації.
Обидва потоки інформації проходять цілим каскадом різноманітних перетворень. Розглянемо найважливіші перетворення цих потоків інформації.
Узгодження рівнів сигналів. Вихідні сигнали датчиків, як правило, не можна передавати безпосередньо в комп'ютер, їх спочатку потрібно узгодити за рівнем. Багато датчиків (наприклад, термоелементи, тензорезистори тощо) мають рівень вихідного сигналу недостатній для передачі каналом зв'язку в комп'ютер, і тому їх потрібно підсилювати. Для підсилення сигналів у сучасних системах автоматичного керування застосовуються операційні підсилювачі, охоплені різними видами зворотних зв'язків. Сучасна електронна промисловість випускає широку гаму типів операційних підсилювачів, як загального призначення, так і спеціалізованих.
Узгодження імпедансів. Крім узгодження сигналів за рівнем, необхідно узгоджувати імпеданси (тобто повні опори) послідовно з'єднаних пристроїв обробки інформації. Пристрій з низьким вхідним опором істотно впливає на процеси, що протікають в об'єкті, до якого він приєднаний. Наприклад, вольтметр з низьким вхідним опором, увімкнений паралельно до пристрою, напругу на якому слід виміряти, спотворює режим досліджуваного кола, оскільки зменшує еквівалентний опір цього кола, в результаті чого напруга на пристрої, до якого приєднаний вольтметр, відрізнятиметься від напруги на пристрої без вольтметра.
Пристрій з високим вихідним імпедансом дуже чутливий до опору навантаження, оскільки навантаження з малим опором спричинює значні вихідні струми, що може призвести до перевантаження пристрою.
Зменшення впливу електромагнітних завад. На роботу систем автоматичного керування негативно впливають завади.
Канали обробки і передачі інформації через взаємні резистивні, індуктивні і ємнісні зв'язки впливають один на одного, чим створюють взаємні завади. Частину сигналу одного каналу, яке через ці зв'язки проникає у розміщений поблизу сусідній канал, часто називають наводкою. Особливо велику за інтенсивністю наводку створюють електричні кола живлення на високочутливі вхідні пристрої систем автоматичного керування.
Зовнішні завади поділяються на промислові, атмосферні і космічного походження.
Аналогова фільтрація. У багатьох випадках смуги частот сигналу і смуги частот завад відомі заздалегідь. Наприклад, частоти вихідних сигналів датчиків температури, тензодатчиків, датчиків вологості лежать у діапазоні від нуля до кількох герц (рідше до десятків герц). Наводка від мережі живлення має, як відомо, частоту коливання 50 Гц. Смуга частот шумів простягається від часток герца до мегагерців.
За допомогою аналогової фільтрації корисні сигнали підсилюються у вибраній смузі частот, а завади, що лежать поза цією смугою, пригнічуються.
Мультиплексування сигналів. Вихідні сигнали багатьох типів датчиків систем автоматичного керування змінюються дуже повільно внаслідок інерційності процесів в об'єктах керування. Швидкодія ж сучасних цифрових пристроїв обробки сигналів дуже велика. Для прикладу можна зазначити, що смуга частот термоперетворювачів становить одиниці герца, у той час як тактова частота цифрових пристроїв обробки інформації (процесорів, контролерів) становить сотні мегагерців. Пропускна здатність сучасних каналів зв'язку також є значною. Таким чином, цифрові пристрої обробки інформації мають таку продуктивність, а канали зв'язку таку пропускну здатність, що можуть одночасно обробляти сотні і тисячі вихідних сигналів датчиків паралельно. Щоб це здійснити, застосовуються мультиплексори.
Дискретизація аналогових сигналів. Вихідні сигнали датчиків є неперервними, тобто існують у будь-який момент часу. Цифрові ж пристрої обробки сигналів обробляють окремі значення сигналів, що наведені у вигляді чисел. Таким чином, на пристрій обробки має надходити не аналоговий сигнал у кожний момент часу, а послідовність окремих значень сигналу через певні інтервали часу. Процес періодичної вибірки окремих значень із аналогового сигналу і представлення неперервного аналогового сигналу послідовністю дискретних значень називається дискретизацією аналогового сигналу.
Вимірювальний перетворювач, який здійснює дискретизацію аналогового сигналу, квантування та кодування сигналу, називається аналого-цифровим перетворювачем (АЦП). Аналого-цифровий перетворювач є невід'ємною складовою частиною будь-якого цифрового приладу. Мікроелектронна промисловість випускає аналого-цифрові перетворювачі у вигляді однієї або кількох мікросхем.
Методи аналого-цифрового перетворення. Методи аналого-цифрового перетворення поділяються на: методи зіставлення; методи зрівноважування.
У методах зіставлення аналого-цифрове перетворення здійснюється за один прийом або такт, тобто з максимальною швидкістю. Щоб домогтися цього, потрібно за допомогою міри відтворити всі N значення, на які квантується діапазон, тобто міра має бути багатоканальною.
У методах зрівноважування аналого-цифрове перетворення здійснюється за кілька тактів. Методи зрівноважування поділяються на методи слідкуючого і розгортального зрівноважування.
Цифрово-аналогове перетворення. У цифрових системах автоматичного керування керівний комп'ютер оперує з сигналами у вигляді двійкових чисел. Щоб передати ці сигнали для керування виконавчими органами, їх потрібно перетворити в аналогову форму. В аналогову форму потрібно також перетворити опорні сигнали для аналогових регуляторів.
Пристрій, який перетворює цифрові сигнали в аналогові, називається цифро-аналоговим перетворювачем (ЦАП).
Цифро-аналогові перетворювачі складаються з опорного джерела напруги з високою стабільністю, матриці резисторів і набору електронних ключів. Використовуються два види матриці резисторів. У матриці пертого виду опір наступного резистора вдвічі більший за опір попереднього. Таким чином, опори резисторів матриці відповідають розрядам двійкового числа. Якщо резистори матриці з'єднати паралельно й увімкнути до опорного джерела стабільної напруги, то через резистори матриці протікатимуть струми, значення яких відповідатимуть розрядам двійкового числа.
2.2.1. Позиційні системи числення, двійкова, вісімкова, шістнадцядкова системи числення. Беззнаковий код цілих чисел. Доповнювальний код цілих чисел. Основні арифметичні операції над цілими числами в беззнаковому та доповнювальному кодах.
Позиційна система числення (або Позиційна нотація) — система числення, в якій значення кожного числового знака (цифри) в запису числа залежить від його позиції (розряду). Таким чином, позиція цифри має вагу у числі. Здебільшого вага кожної позиції кратна деякому натуральному числу b, b>1, яке називається основою системи числення.
Двійкова система числення — це позиційна система числення, база якої дорівнює двом та використовує для запису чисел тільки два символи: зазвичай 0 (нуль) та 1 (одиницю).
Вісімкова система числення — позиційна цілочисельна система числення з основою 8. Для представлення чисел в ній використовуються цифри від 0 до 7.
Шістнадцяткова система числення — це позиційна система числення з основою 16. Тобто кожне число в ній записується за допомогою 16 символів. Арабські цифри від 0 до 9 відповідають значенням від нуля до дев'яти, а 6 літер латинської абетки A, B, C, D, E, F відповідають значенням від десяти до п'ятнадцяти.
У МП двійкові коди (ДК) використовуються для подання будь-яких даних, що обробляються: чисел, тексту, команд і т. д. При цьому розрядність ДК може перевищувати розрядність внутрішніх регістрів самого процесора і комірців використовуваної пам'яті. У такому випадку довгий код може займати кілька комірок пам'яті і оброблятися кількома командами процесора. Всі комірки пам'яті, виділені під багатобайтний ДК, розглядаються як одне число.
Правила виконання арифметичних дій над двійковими числами задаються таблицею1. Правила арифметики в усіх позиційних системах аналогічні.
Таблиця 1. - Правила виконання арифметичних дій над двійковими числами
Двійкове додавання |
Двійкове віднімання |
Двійкове множення |
0+0=0 0+1=1 1+0=1 1+1=10 |
0-0=0 1-0=1 1-1=0 10-1=1 |
0*0=0 0*1=0 1*0=0 1*1=1 |
Додавання двох чисел в двійковій системі можна виконувати стовпцем, складаючи або дві цифри молодшого розряду, або дві цифри чисел, які додаються, в даному розряді і одиниці перенесення з сусіднього молодшого розряду.
Наприклад,
1111101
+ 101101.01
11011.01
-------------------
1001000.10
Числа в двійковій системі віднімаються аналогічно числам в десятковій системі. При відніманні чисел в даному розряді, якщо цифра, що зменшується, менше цифри числа, що віднімається, позичають одиницю з наступного старшого розряду. При цьому одиниця, що позичається із старшого розряду, рівна двом одиницям даного розряду.
Наприклад,
10101.11
- 1011.01
---------------
1010.10
При здійсненні обчислень, звичайно, доводиться мати справу не тільки з цілими невід’ємними числами, але також з від’ємними.
У програмуванні виділяють два типи чисел: беззнакові та знакові. Всі беззнакові числа вважаються невід’ємними, і всі їх розряди використовуються для задання абсолютної величини числа. Так, за допомогою одного байту можна закодувати цілі беззнакові числа від 0 до 255.
Для представлення ж від’ємних чисел слід виділити один біт для знаку. Як правило, це старший біт. Якщо один біт в числі виділяється під його знак, таке число називається знаковим. Як правило, 0 у старшому (крайньому зліва) біті відповідає додатнім числам, а 1 - від’ємним.
Представлення від’ємних чисел залежить від кількості байтів, яка відводиться на число. Для визначеності будемо розглядати однобайтові знакові числа.
Виділяють три основних способи представлення від’ємних чисел:
прямий код, який утворюється з коду відповідного додатного числа шляхом встановлення знакового біта в 1;
обернений код, який утворюється шляхом заміни значення кожного біта на протилежне;
додатковий код, який утворюється шляхом додавання 1 до молодшого біта оберненого коду.
Приклад. Розглянемо число -3. Двійковим еквівалентом відповідного додатного числа 3 є 00000011.
Прямий код. Встановимо знаковий біт в 1 (нагадаємо, що 1 в старшому біті знакового числа сигналізує про його від’ємність). Всі інші біти залишаються без змін. В результаті вийде 10000011.
Обернений код. Замінимо кожний біт на протилежний (1 на 0; 0 на 1); результатом буде 11111100.
Додатковий код. Додамо 1 до оберненого коду; в результаті вийде 11111101. Зверніть увагу, що якщо розглядати послідовність 11111101 як беззнакове, а не як знакове число, вона інтерпретується як додатнє число 253.
Приклад 1. Числа А, –А, С и –С представити в прямому, оберненму (зворотньому), доповнюваному кодах.
А = 30710 = 1001100112 С = 9110 = 10110112
[A]пр = [A]об = [A]дк = 0|000000100110011
[–A]пр = 1|000000100110011
[–A]об = 1|111111011001100
[–A]дк = 1|111111011001100+1 = 1|111111011001101
[C]пр = [C]об = [C]дк = 0|000000001011011
[–C]пр = 1|000000001011011
[–C]об = 1|111111110100100
[–C]дк = 1|111111110100100+1 = 1|111111110100101
Приклад 2. Обчислити: А + B, A – B, –A – B. Нехай А=16010, B=4510.
[A]дк = 0|000000010100000
[–A]дк = 1|111111101100000
[B]дк = 0|000000000101101
[–B]дк = 1|111111111010011
|
А + B |
|
|
A – B |
|
|
–A – B |
+ |
0|000000010100000 |
|
+ |
0|000000010100000 |
|
+ |
1|111111101100000 |
0|000000000101101 |
|
1|111111111010011 |
|
1|111111111010011 |
|||
|
0|000000011001101 |
|
|
0|000000001110011 |
|
|
1|111111100110011 |
Приклад 3. Виконати додавання чисел, представленних в машинних кодах: A+C; –A+C; A+(– C); –A+(– C).
A = 30710 =1001100112 С = 9110 = 10110112
[A]дк = 0|000000100110011
[–A]дк = 1|111111011001101
[C]дк = 0|000000001011011
[–C]дк = 1|111111110100101
|
А + C |
|
|
–A + C |
+ |
0|000000100110011 |
|
+ |
1|111111011001101 |
0|000000001011011 |
|
0|000000001011011 |
||
|
0|000000110001110 |
|
|
1|111111100101000 |
|
А + (– C) |
|
|
–A + (– C) |
+ |
0|000000100110011 |
|
+ |
1|111111011001101 |
1|111111110100101 |
|
1|111111110100101 |
||
|
0|000000011011000 |
|
|
1|111111001110010 |
Зауваження. В ЕОМ операції віднімання, множення, ділення здійснюються за допомогою операції додавання. Наприклад, при відніманні від'ємник записується у доповняльному коді і віднімання заміняється додаванням.
Приклад 4: 23 + 22 = 45
Приклад 5: 23 - 13 = 23 + (-13 ) = 10
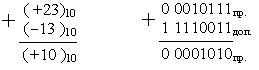
(-13)10 = (1 0001101)пр. = (1 1110010)об. = (1 1110011)доп.
Приклад 6: 7 - 13 = 7 + (-13) = -6
Оскільки результат від'ємний (біт знаку містить одиницю), то він представлений у доповняльному коді. Для перевірки правильності виконання операції потрібно перейти до прямого коду, який визначає абсолютне значення результату. Для цього потрібно:
1. відняти від доповняльного кода 1: 11111010дк. - 00000001 = 11111001об.
2. проінвертувати обернений код для переходу до прямого: 10000110пр.
Приклад 7: (- 7 – 13) = (-7) +(-13) = -20
|
|
||||||||||||||||
1 0010100пр. - прямий двійковий код числа ( -20 )10