
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4 Элементарные преобразования строк (столбцов) матрицы
- •Вопрос 5 Нахождение обратной матрицы методом элементарных преобразований
- •Вопрос 6 Теория систем линейных алгебраических уравнений(слау)
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9 Однородные слау (ослау)
- •Вопрос 10
- •Построение нормальной системы решений (нср)
- •Вопрос 11
- •Вопрос 12 Общее решение неоднородных слау(нслау)
- •Вопрос 13 Определение линейного пространства (лп). Примеры.
- •I. Сложение
- •II. Умножение
- •III. Аксиомы дистрибутивности
- •Вопрос 14 лз и лнз системы векторов
- •Вопрос 15 Базис и размерность лп.
- •Вопрос 16 Линейные подпространства. Линейные оболочки. Размерность линейной оболочки.
- •Вопрос 17 Координаты вектора в базисе.
- •Вопрос 18
- •Вопрос 19 Сумма и пересечение линейных подпространств.
- •Вопрос 20 Матрица перехода от одного базиса к другому.
- •Вопрос 21 Линейные формы (линейные функционалы). Их свойства. Сопряженное пространство. Биортогональный базис.
- •Вопрос 22
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32 Билинейные формы
- •Общий вид бф
- •Преобразование матрицы бф при смене базиса
- •Вопрос 33 Квадратичные формы
- •Общий вид кф
- •Вопрос 34
- •Вопрос 35 Закон инерции кф
- •Вопрос 36 Классификация квадратичных форм в вещественном лп
- •Вопрос 37 Полуторалинейные формы в комплексном лп
- •Общий вид пф
- •Вопрос 38
- •Неравенство Коши-Буняковского
- •Вопрос 39 Общий вид сп в веп и кеп
- •Вопрос 40 Ортонормированный базис в веп и кеп
- •Вопрос 41
- •Вопрос 42 Ортогональные дополнения линейных подпространств в
- •Вопрос 43
- •Вопрос 44 Линейные, полуторалинейные и билинейные формы
- •Вопрос 45
- •Сопряженный оператор и его свойства
- •Свойства сопряженного оператора
- •Вопрос 46 Нормальные операторы (но) и их свойства.
- •Вопрос 47 Самосопряженные операторы
- •Вопрос 48
- •Вопрос 49 Спектральная теорема для нормальных операторов и нормальных матриц
- •Спектральная теорема для самосопряженных операторов и эрмитовых (симм.) матриц
- •Спектральная теорема для унитарных операторов и унитарных (ортог.) матриц
- •Вопрос 50 Приведение эрмитовой квадратичной формы к главным осям унитарным преобразованием
Вопрос 11
Пусть (10) А .
Опр. Упорядоченная ЛНЗ система решений ОСЛАУ … называется фундаментальной системой решений(ФСР) , если
Замеч.
Если
…
решением
будет
где
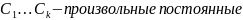
Теор. (о ФСР ОСЛАУ)
Если Rg A = r<n, то (10) обладает ФСР
Любая ФСР ОСЛАУ имеет (n-r) элементов
Любые (n-r) ЛНЗ упорядоченных решений (10) образуют ее ФСР
Если …
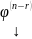 произвольные ФСР ОСЛАУ (10),
то
произвольные ФСР ОСЛАУ (10),
то
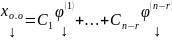
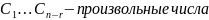
Док-во:
1) следует из того, что при r<n НСР, которая является ФСР
2)
Рассм. мн-во всевозм. Реш-ий ОСЛАУ.
Выясним, что совокупность всех реш-ий
явл. ЛП (назовем его Х). Опред. ФСР этой
с-мы удовл. всем св-вам базиса. Т.о., ФСР
явл. базисом в Х. В частности, НСР – базис
в Х. НСР содержит (n-r)
элементов
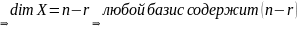 элементов
любая
ФСР содержит (n-r)
элементов
элементов
любая
ФСР содержит (n-r)
элементов
3) любая ЛНЗ с-ма из (n-r) эл-тов будет базисом в Х любая ЛНЗ с-ма из (n-r) реш-ий будет ФСР
4) смотри замечание к определению ФСР
Вопрос 12 Общее решение неоднородных слау(нслау)
Рассмотрим
(1) А
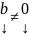
Теор.(О структуре общего решения НСЛАУ)
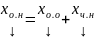 ,
где хо.о
– общее решение ОСЛАУ, хч.н.
– частное решение
,
где хо.о
– общее решение ОСЛАУ, хч.н.
– частное решение
Док-во:
Пусть
Rg
A=r=n.
Тогда методом элементарных преобразований
она приводится к виду
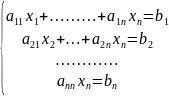
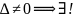 Решение(
Решение(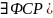 (
(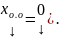 Т.е.
Т.е.
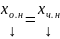
Пусть
Rg
A<n.
Покажем, что
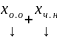 является решением (1) А(
является решением (1) А(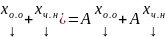 =
= .
Покажем, что решение (1) входит в (2). Пусть
.
Покажем, что решение (1) входит в (2). Пусть
 произвольное
решение (1), а
произвольное
решение (1), а
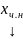 -
какое-либо частное решение. Тогда
-
какое-либо частное решение. Тогда
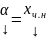 А(
А(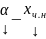 )=
)=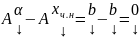
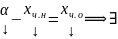
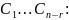
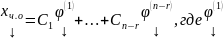 …
произвольные
ФСР ОСЛАУ А
…
произвольные
ФСР ОСЛАУ А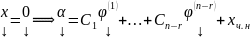 ,
т.е. любое решение можно представить в
таком виде
,
т.е. любое решение можно представить в
таком виде
Вопрос 13 Определение линейного пространства (лп). Примеры.
Рассмотрим множество k, состоящее не менее, чем из двух элементов.
Опр.
k
называется полем, если
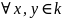 введены операции «сложения» и «умножения»,
не выводящие из k,
т.е.
введены операции «сложения» и «умножения»,
не выводящие из k,
т.е.
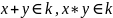 ,
удовлетворяющие следующим свойствам
(аксиомам поля):
,
удовлетворяющие следующим свойствам
(аксиомам поля):
I. Сложение
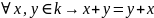 (коммутативность)
(коммутативность)
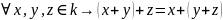 (ассоциативность)
(ассоциативность)
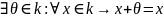 (существование
нейтрального элемента)
(существование
нейтрального элемента)
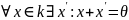 (существование
противоположного элемента)
(существование
противоположного элемента)
II. Умножение
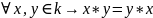
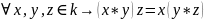
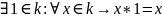
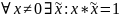
III. Аксиомы дистрибутивности
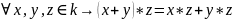
Пример ℝ, ℚ, ℂ - поля, ℤ - не поле.
Далее
рассматриваются
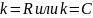 .
.
Опр.
Множество элементов произвольной
природы V,
для элементов которого определены
операции сложения и умножения на элементы
поля k,
не выводящие из V
(т.е.
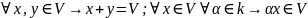 ),
называется линейным пространством над
полем k,
если выполнены следующие свойства
(аксиомы ЛП):
),
называется линейным пространством над
полем k,
если выполнены следующие свойства
(аксиомы ЛП):
1º
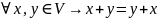 (коммутативность)
(коммутативность)
2º
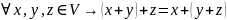 (ассоциативность)
(ассоциативность)
3º
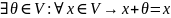 (существование нейтрального элемента)
(существование нейтрального элемента)
4º
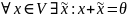 (существование противоположного
элемента)
(существование противоположного
элемента)
5º
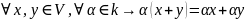 (дистрибутивность относительно суммы
элементов V)
(дистрибутивность относительно суммы
элементов V)
6º
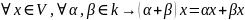 (дистрибутивность относительно суммы
элементов поля k)
(дистрибутивность относительно суммы
элементов поля k)
7º
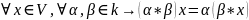
8º
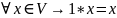
Замеч.
Если
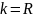 ,
то
,
то
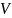 называется
действительным ЛП; если
называется
действительным ЛП; если
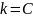 ,
то
называется комплексным ЛП.
,
то
называется комплексным ЛП.
Теор. (свойства нейтральных и противоположных элементов)
1º
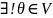
2º
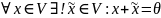
3º
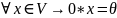
4º
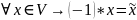
5º
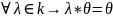
Замеч. Далее элементы поля k будем называть скалярами и обозначать преимущественно греческими буквами, а элементы ЛП будем называть векторами и обозначать латинскими буквами без стрелок.
#1º
(от
противного) Пусть
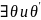 -
нейтральные элементы, тогда
-
нейтральные элементы, тогда
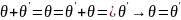
2º
Пусть
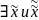 –
противоположные элементы для x,
тогда
–
противоположные элементы для x,
тогда
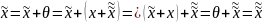
3º
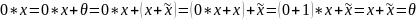
4º
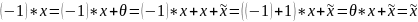
5º
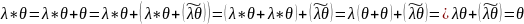 #
#
Примеры.
1) ЛПВпр, ЛПВпл, ЛПВ – изучены в курсе АГ.
2)
ЛП строк (или столбцов) длины (высоты)
n:
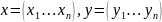
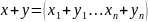
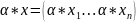
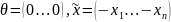
Остальные свойства также выполнены.
Такое
ЛП обозначают
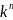 .
В частности, при n=1
получаем, что поле k
также является ЛП. В частности, ℝ и ℂ -
ЛП.
.
В частности, при n=1
получаем, что поле k
также является ЛП. В частности, ℝ и ℂ -
ЛП.
3)
Совокупность
всевозможных решений ОСЛАУ. Если
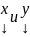 - решения, то
- решения, то
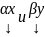 тоже решение
тоже решение
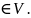
 - является
решением;
- является
решением;
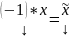 также является решением. Остальные
свойства являются свойствами столбцов.
также является решением. Остальные
свойства являются свойствами столбцов.
4)
Прямоугольные
матрицы размером (m*n)
c
обычными операциями сложения и умножения
на числа
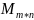
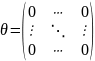 ;
;
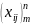 ;
;
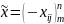
Остальные свойства ЛП выполняются, исходя из свойств линейных операций с матрицами
5)
Всевозможные
многочлены степени
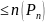
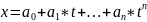 ,
,
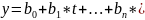
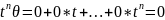 ,
,
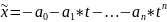
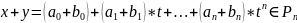
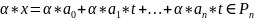
6)
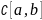 – множество функций, непрерывна на
– множество функций, непрерывна на
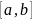 с операциями:
с операциями:
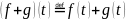
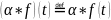
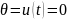
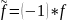
7)
Пусть
V
и
W
– ЛП над полем k.
Их декартовым произведением называется
совокупность всевозможных пар x
и y
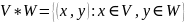 ,
причем
,
причем
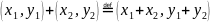 ,
,
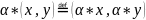 .
Декартово произведение V
и
W
образует
ЛП:
.
Декартово произведение V
и
W
образует
ЛП:
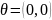 .
Если
.
Если
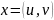 ,
то
,
то
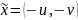 .
В частности, если
.
В частности, если
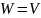 ,
то
,
то
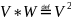 ,
в
частности,
,
в
частности,
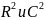 .
.
