Вопрос 8

Теорема Кронекера-Капелли. С-ма (1) 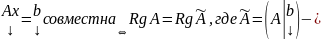расширенная матрица СЛАУ (1) (т.е. с-ма совметна ранг основной = рангу расширенной)

Док-во

Пусть с-ма совместна. Приводим её расшир. матр. к ТФ (в обл. A’). Тогда .

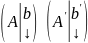(A’ – ТФ для А). Поскольку Rg A=r, то 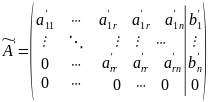(с-ма

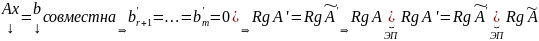
Пусть 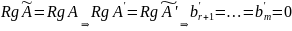(т.к. иначе найдется невырожденный минор (r+1) порядка у расширенной матрицы) 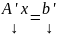-совм. 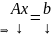тоже совместна.

Вопрос 9 Однородные слау (ослау)

Рассмотрим СЛАУ А (1), если 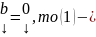однородная СЛАУ, в противном случае она неоднородная. Пусть (1₀) А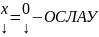 . Эта система всегда обладает нулевым (тривиальным) решением

Опр. Всякое решение ОСЛАУ, отличное от тривиального, называется нетривиальным

Теор. (Линейной свойство решений ОСЛАУ)

Пусть 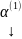… 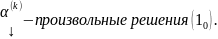Тогда 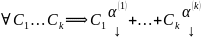тоже является решением (1₀)

Док-во: А(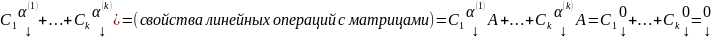

След. Если (1₀) имеет по крайней мере одно нетривиальное решение, то она имеет бесконечно много нетривиальных решений

Док-во:

Т.к. 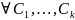– любые числа.

Теор. (О существовании нетривиального решения ОСЛАУ)

Пусть Rg A=r, а число неизвестных в системе =n 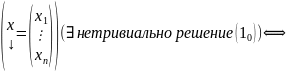Rg A<n, т.е.r<n

Док-во: 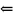. Пусть r<n. Приведем А к ТФ. Пусть это А`. Тогда Rg A`=r.Запишем эквивалентную СЛАУ, перенеся (n-r) св. переменных в правую часть

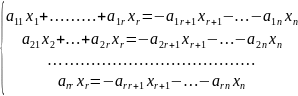1. СЛАУ (2) эквивалентно (1₀), т.е. имеет те же решения. Придадим св. переменным значения: x_r+1=…=x_n-1=0, x_n=1. По теореме Крамера (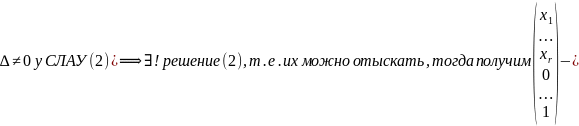 нетривиальное решение (1₀)

Пусть существует нетривиальное решение (1₀). Тогда обязательно Rg A=r<n. Т.к. если бы r=n, то (1₀) стала бы (3)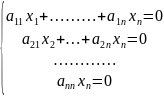 ( 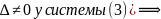имеет только тривиальные решения (по теореме Крамера) 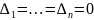(тогда и (1₀) имеет только тривиальные решения - противоречие )

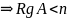
Вопрос 10

Пусть (1₀) А .

Опр. Решения 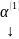… 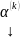ОСЛАУ наз. ЛЗ, если нетривиальная ЛК 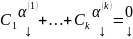(4). Система решений называется ЛНЗ, если (4) выполняется только если

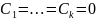
Опр. Упорядоченная ЛНЗ система решений ОСЛАУ 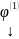… 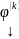называется фундаментальной системой решений(ФСР) , если

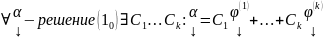
Замеч. Если …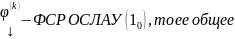 решением будет 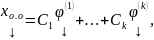где

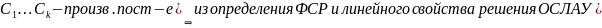
Док-во:

Следует из опр. ФСР и лин.св-в реш-ий ОСЛАУ

Построение нормальной системы решений (нср)

Пусть Rg A=r. Приведем ее к ТФ А`(Rg A`=r). Пусть r<n. Тогда (n-r) свободных переменных преобразуют СЛАУ перенос в правую часть. Получим СЛАУ (2). Присвоим свободным переменным следующий набор значений. n-r штук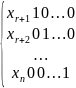

Всего n-r наборов

Замеч. Если n-r=1, тогда получаем, x_r+1=1. Для каждого такого набора найдем из (2) соответствующее значение главных пер.(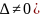

Тогда получаем всего (n-r) наборов решений 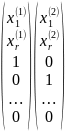… 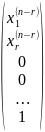. Имеем упорядоченную систему решений ОСЛАУ(1₀). Покажем, что столбцы-решения являются ЛНЗ. Рассмотрим матрицу 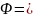… 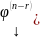. Ее минор 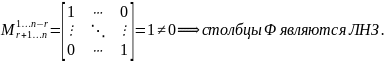Покажем, что любое решение ОСЛАУ (1₀) может быть представлено линейной комбинацией …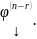 Пусть =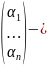 произвольное решение (1₀).

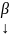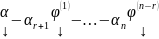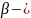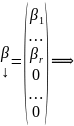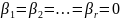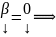Рассмотрим = . Тогда решение (1₀) т.к. является ЛК решений. Заметим, что это решение, свободные переменные которого нулевые. Найдем по ним основные переменные(из(2)), получим , таким образом, любое решение есть ЛК построенной системы, т.е.

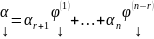
Опр. Построенная система решений называется нормальной (НСР). Очевидно, что она является ФСР(в соответствии с определением ФСР)