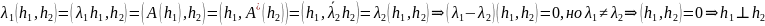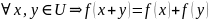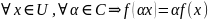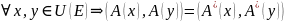- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4 Элементарные преобразования строк (столбцов) матрицы
- •Вопрос 5 Нахождение обратной матрицы методом элементарных преобразований
- •Вопрос 6 Теория систем линейных алгебраических уравнений(слау)
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9 Однородные слау (ослау)
- •Вопрос 10
- •Построение нормальной системы решений (нср)
- •Вопрос 11
- •Вопрос 12 Общее решение неоднородных слау(нслау)
- •Вопрос 13 Определение линейного пространства (лп). Примеры.
- •I. Сложение
- •II. Умножение
- •III. Аксиомы дистрибутивности
- •Вопрос 14 лз и лнз системы векторов
- •Вопрос 15 Базис и размерность лп.
- •Вопрос 16 Линейные подпространства. Линейные оболочки. Размерность линейной оболочки.
- •Вопрос 17 Координаты вектора в базисе.
- •Вопрос 18
- •Вопрос 19 Сумма и пересечение линейных подпространств.
- •Вопрос 20 Матрица перехода от одного базиса к другому.
- •Вопрос 21 Линейные формы (линейные функционалы). Их свойства. Сопряженное пространство. Биортогональный базис.
- •Вопрос 22
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32 Билинейные формы
- •Общий вид бф
- •Преобразование матрицы бф при смене базиса
- •Вопрос 33 Квадратичные формы
- •Общий вид кф
- •Вопрос 34
- •Вопрос 35 Закон инерции кф
- •Вопрос 36 Классификация квадратичных форм в вещественном лп
- •Вопрос 37 Полуторалинейные формы в комплексном лп
- •Общий вид пф
- •Вопрос 38
- •Неравенство Коши-Буняковского
- •Вопрос 39 Общий вид сп в веп и кеп
- •Вопрос 40 Ортонормированный базис в веп и кеп
- •Вопрос 41
- •Вопрос 42 Ортогональные дополнения линейных подпространств в
- •Вопрос 43
- •Вопрос 44 Линейные, полуторалинейные и билинейные формы
- •Вопрос 45
- •Сопряженный оператор и его свойства
- •Свойства сопряженного оператора
- •Вопрос 46 Нормальные операторы (но) и их свойства.
- •Вопрос 47 Самосопряженные операторы
- •Вопрос 48
- •Вопрос 49 Спектральная теорема для нормальных операторов и нормальных матриц
- •Спектральная теорема для самосопряженных операторов и эрмитовых (симм.) матриц
- •Спектральная теорема для унитарных операторов и унитарных (ортог.) матриц
- •Вопрос 50 Приведение эрмитовой квадратичной формы к главным осям унитарным преобразованием
Вопрос 44 Линейные, полуторалинейные и билинейные формы
Лемма.(О скалярном произведении)
Пусть
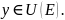 Если
Если
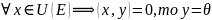
Док-во:
Поскольку
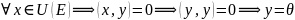
След.
Если
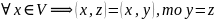
Док-во:

Опр.
Закон(правило)(функция) f,
ставящая любому элементу из
в
соответствие комплексное число (т.е. f
:
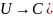 называется
линейной формой(функционалом) (ЛФ) в
,
если
:
называется
линейной формой(функционалом) (ЛФ) в
,
если
:
Теор. (О представлении ЛФ в
ЛФ
f,
действующая в
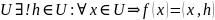 (h
фиксирован и не зависит от x
) – т.е. для всех х он один о тот же и
определяется только самой формой f
(h
фиксирован и не зависит от x
) – т.е. для всех х он один о тот же и
определяется только самой формой f
Док-во:
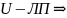 в
нем
ОНБ. Пусть это Е={e1…eк}.
Возьмем произвольные
в
нем
ОНБ. Пусть это Е={e1…eк}.
Возьмем произвольные
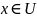 и
разложим его по базису :
и
разложим его по базису :
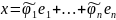 ,
тогда :
,
тогда :
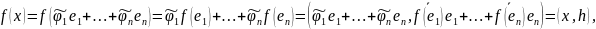 где
где
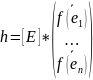 определяется только действием f
на базовые элементы и не зависит от x.
Докажем единственность: Пусть
определяется только действием f
на базовые элементы и не зависит от x.
Докажем единственность: Пусть
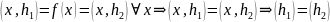
Замеч.
Аналогичные определения и утверждения
имеют место в
,
только
так : f
:
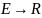
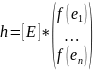
Рассмотрим ПФ в
Опр.
ПФ
в
–
это правило В :
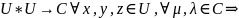
B(
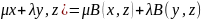
B(
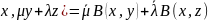
Теор.
ПФ В, действ. В
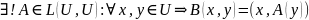
Док-во:
При фиксированном
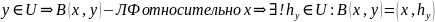 Определяем А следующим образом :
Определяем А следующим образом :
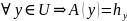 Покажем, что А – ЛО (т.е.
Покажем, что А – ЛО (т.е.
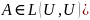 Пусть
x
– произвольный элемент из
,
тогда
Пусть
x
– произвольный элемент из
,
тогда
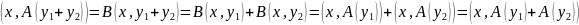 В силу произвольности х получим :
В силу произвольности х получим :
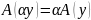 Покажем, что
Покажем, что
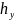 определяется единственным образом :
определяется единственным образом :
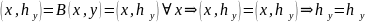 Аналогично А тоже определяется
единственным образом : Если
Аналогично А тоже определяется
единственным образом : Если
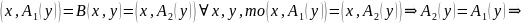
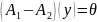
Вопрос 45
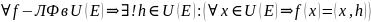
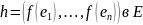
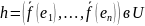
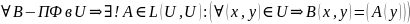
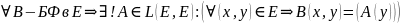
Сопряженный оператор и его свойства
Опр.
А*
назовем оператором, сопряженным к А в
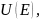 если
если
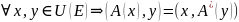
Теор. ( О существовании и единственности сопряженного оператора и его линейности)
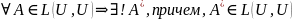
Док-во:
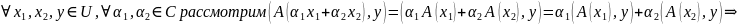 имеет
место полная линейность по первому
аргументу. СП в
полулинейно
по второму аргументу
имеет
место полная линейность по первому
аргументу. СП в
полулинейно
по второму аргументу
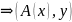 является ПФ в
является ПФ в
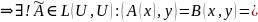 В силу произвольности x,y,
получаем
В силу произвольности x,y,
получаем
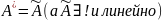
Теор. ( для евклидового аналогично)
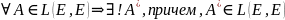
ДОКАЗАТЬ
Опр.
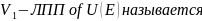 инвариантным
относительно А , если
инвариантным
относительно А , если
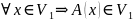 (где
(где
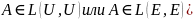
Свойства сопряженного оператора
I*=I
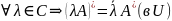
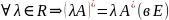
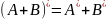
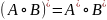
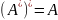
 инвариантно
относительно
инвариантно
относительно
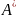
Если А – обратим, то тоже обратим, причем
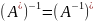
Если Е – ОНБ, то
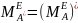
Док-во всех свойств сопряженного оператора:
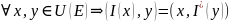
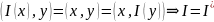
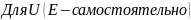
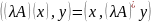
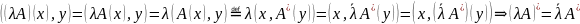
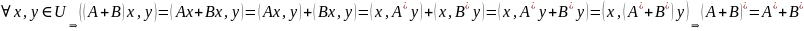
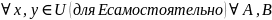
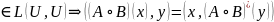
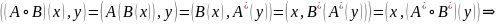
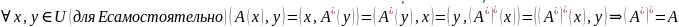
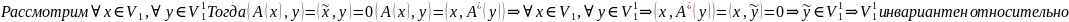
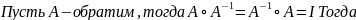 I=
I*
I=
I*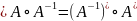 с одной стороны. С другой стороны I=
I*
=
с одной стороны. С другой стороны I=
I*
=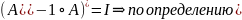 обратного оператора
обратного оператора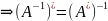
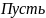 Е={e1…en}
ОНБ в
Е={e1…en}
ОНБ в
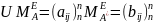 Тогда
Тогда
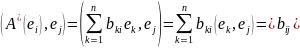
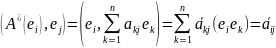 Таким образом,
Таким образом,
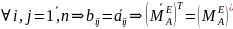 (В
аналогично,
но там нет комплексного сопряжения)
(В
аналогично,
но там нет комплексного сопряжения)
Вопрос 46 Нормальные операторы (но) и их свойства.
Опр.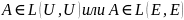 называется
нормальным, если
называется
нормальным, если
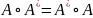
Опр.
Действительная матрица называется
нормальной, если
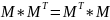
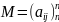 Комплексная матрица называется
нормальной, если
Комплексная матрица называется
нормальной, если
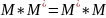
Теор.(Свойства НО)
Сл.
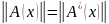
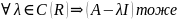 норм.
норм.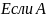 имеет
СВ h
и СЗ
,
то для
имеет
СВ h
и СЗ
,
то для
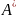 h
также является СВ с СЗ
h
также является СВ с СЗ
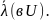
Замеч. В СВ и СЗ норм. А и совпадают
Пусть h – собственный вектор НО А. Тогда L=Span(h) и
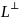 является инвариантным относительно
обоих операторов А и
является инвариантным относительно
обоих операторов А и
А – нормален
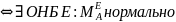
Сл. В любом ОНБ матрица нормального оператора нормальна
Если
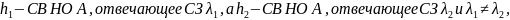 то
то
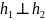
Док-ва свойств:
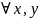 рассмотрим
рассмотрим
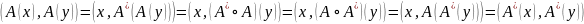
Cл.
: Если y=x,
то :
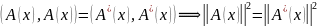
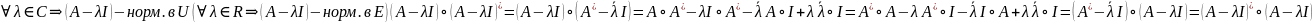 (в
аналогично,
но без к.с.)
(в
аналогично,
но без к.с.)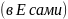 В
. Пусть
h
– СВ А СЗ
В
. Пусть
h
– СВ А СЗ
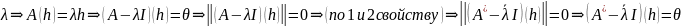
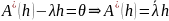
Пусть h – собственный вектор НО А. L=Span(h) Тогда
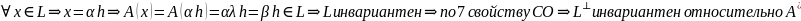 Рассмотрим
Рассмотрим

Пусть Е – ОНБ в
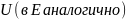 А
А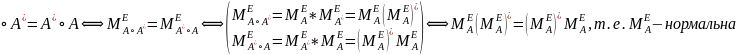
Пусть
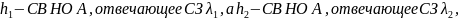 тогда
тогда