- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4 Элементарные преобразования строк (столбцов) матрицы
- •Вопрос 5 Нахождение обратной матрицы методом элементарных преобразований
- •Вопрос 6 Теория систем линейных алгебраических уравнений(слау)
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9 Однородные слау (ослау)
- •Вопрос 10
- •Построение нормальной системы решений (нср)
- •Вопрос 11
- •Вопрос 12 Общее решение неоднородных слау(нслау)
- •Вопрос 13 Определение линейного пространства (лп). Примеры.
- •I. Сложение
- •II. Умножение
- •III. Аксиомы дистрибутивности
- •Вопрос 14 лз и лнз системы векторов
- •Вопрос 15 Базис и размерность лп.
- •Вопрос 16 Линейные подпространства. Линейные оболочки. Размерность линейной оболочки.
- •Вопрос 17 Координаты вектора в базисе.
- •Вопрос 18
- •Вопрос 19 Сумма и пересечение линейных подпространств.
- •Вопрос 20 Матрица перехода от одного базиса к другому.
- •Вопрос 21 Линейные формы (линейные функционалы). Их свойства. Сопряженное пространство. Биортогональный базис.
- •Вопрос 22
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32 Билинейные формы
- •Общий вид бф
- •Преобразование матрицы бф при смене базиса
- •Вопрос 33 Квадратичные формы
- •Общий вид кф
- •Вопрос 34
- •Вопрос 35 Закон инерции кф
- •Вопрос 36 Классификация квадратичных форм в вещественном лп
- •Вопрос 37 Полуторалинейные формы в комплексном лп
- •Общий вид пф
- •Вопрос 38
- •Неравенство Коши-Буняковского
- •Вопрос 39 Общий вид сп в веп и кеп
- •Вопрос 40 Ортонормированный базис в веп и кеп
- •Вопрос 41
- •Вопрос 42 Ортогональные дополнения линейных подпространств в
- •Вопрос 43
- •Вопрос 44 Линейные, полуторалинейные и билинейные формы
- •Вопрос 45
- •Сопряженный оператор и его свойства
- •Свойства сопряженного оператора
- •Вопрос 46 Нормальные операторы (но) и их свойства.
- •Вопрос 47 Самосопряженные операторы
- •Вопрос 48
- •Вопрос 49 Спектральная теорема для нормальных операторов и нормальных матриц
- •Спектральная теорема для самосопряженных операторов и эрмитовых (симм.) матриц
- •Спектральная теорема для унитарных операторов и унитарных (ортог.) матриц
- •Вопрос 50 Приведение эрмитовой квадратичной формы к главным осям унитарным преобразованием
Вопрос 40 Ортонормированный базис в веп и кеп
Пусть – УП
Опр.
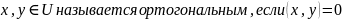
Аналогичная формулировка и для
Пусть
{e1…en}
– система элементов. Назовем ее
ортогональной(ОС), если
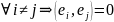 (т.е.
ее элементы попарно ортогональны). Если
же выполнено, что
(т.е.
ее элементы попарно ортогональны). Если
же выполнено, что
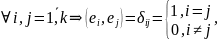 то система называется ортонормированной(ОНБ)
то система называется ортонормированной(ОНБ)
Опр.
ОС называется ортогональным базисом
(ОБ), если она является базисом в
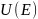
Опр. ОНС называется ортонормированным базисом(ОНБ), если она является базисом в
Замеч.
а) Если Е – ОБ, то
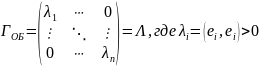 (x,y)=
(x,y)=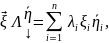 где
где
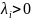
б)
Если Е – ОНБ, то
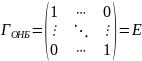 (x,y)=
(x,y)=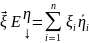
Теор. (О ЛНЗ ОС ненулевых элементов)
Пусть
{e1…ek}-ОС
: (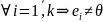 Тогда эта ОС является ЛНЗ
Тогда эта ОС является ЛНЗ
Док-во:
Составим ЛК
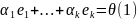
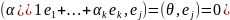
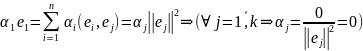 т.е.
(1) возможно
т.е.
(1) возможно
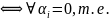
{e1…ek} – ЛНЗ
Теор. (Критерий ОНБ)
Пусть
x,y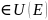 , Е – базис в нем. Тогда (Е – ОНБ)
, Е – базис в нем. Тогда (Е – ОНБ)
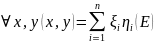
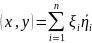 (
(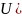
где x=[E]
Док-во:
ВЕП
Пусть Е – ОНБ
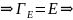 (x,y)=
(x,y)=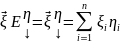
Пусть
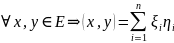 Возьмем x=ek,
y=em
(ek,
em)=
((0…1..0),(0…1…0))=(0…1…0)
Возьмем x=ek,
y=em
(ek,
em)=
((0…1..0),(0…1…0))=(0…1…0)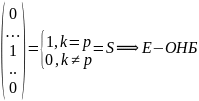
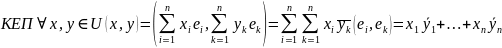 .
Выразим координаты
.
Выразим координаты
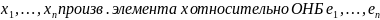 .
Умножая разложение этого элемента по
базису
.
Умножая разложение этого элемента по
базису
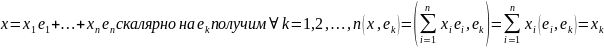
Вопрос 41
Теор.
(О построении ОНБ из произвольного
базиса
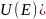
В любом евклидовом(унитарном) ЛП ОНБ, причем из произвольного базиса Е={e1…en} ОНБ может быть построен следующим образом:
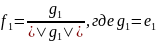
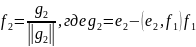
…
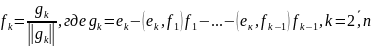
Док-во:
Рассмотрим
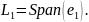 В нем существует ОНБ, состоящий из одного
элемента
В нем существует ОНБ, состоящий из одного
элемента
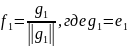 В самом деле
В самом деле
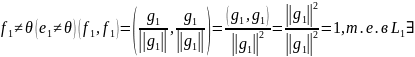 ОНБ {f1}.
Рассмотрим теперь
ОНБ {f1}.
Рассмотрим теперь
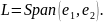 Строим
Строим
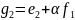 ,
где
,
где
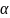 выбираем таким образом, чтобы
выбираем таким образом, чтобы
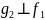 Тогда (
Тогда (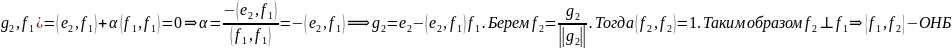 .
Пусть доказано, что
.
Пусть доказано, что
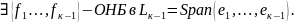 Покажем, что тогда
ОНБ в
Покажем, что тогда
ОНБ в
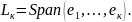 Возьмем
Возьмем
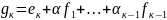 .
Заметим, что
.
Заметим, что
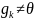 (
иначе
(
иначе
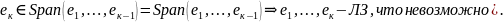 Выбираем теперь чтобы
Выбираем теперь чтобы
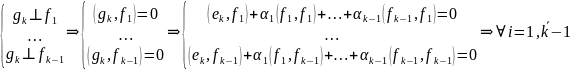
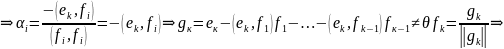
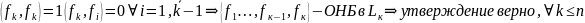
Замеч. Метод построения ортонормированных базисов из произвольного базиса называется методом ортогонализации по Шмидту
Замеч. Подобным образом любая ЛНЗ система векторов может быть преобразована в ОС(ОНС)
Вопрос 42 Ортогональные дополнения линейных подпространств в
Пусть
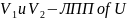 Будем
говорить, что
Будем
говорить, что
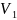 ортогонально
ортогонально
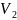 ,
если
,
если
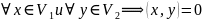
Замеч.
Очевидно, что если
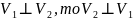 ,
т.е. эти ЛПП взаимно ортогональны
,
т.е. эти ЛПП взаимно ортогональны
Теор.(О пересечении ортогональных ЛПП)
Если
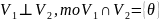
Док-во:
Пусть
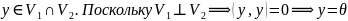
Опр.
Ортогональными дополнениями ЛПП
до
называется
множество элементов
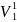 :
:
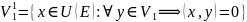
Теор. (Об ортогональности дополнений)
также
является ЛПП of
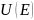
Док-во:
Пусть x,
z
– произвольные элементы из
.
Тогда
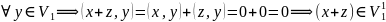 .
Пусть
.
Пусть
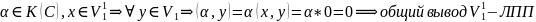
Лемма.
Пусть
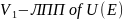 и
Е={e1…eк}-ОНБ
в нем. Тогда (
и
Е={e1…eк}-ОНБ
в нем. Тогда (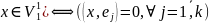
Док-во:
Пусть
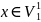 ,
тогда
,
тогда
 Берем в качестве
Берем в качестве
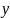 последовательно
e1…eк
;
получаем
последовательно
e1…eк
;
получаем
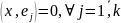
Пусть
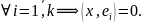 Возьмем произвольный
Возьмем произвольный
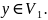 Тогда
Тогда
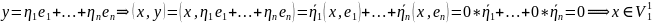
Вопрос 43
Теор.( О разложении в прямую сумму своего ЛПП и его ортогональные дополнения)
Пусть
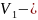 произвольное
ЛПП
произвольное
ЛПП
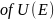 ,
тогда
:
,
тогда
:
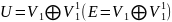 ,
т.е.
,
т.е.
(Опр.)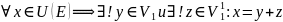 при
этом y
называется ортогональной проекцией x
на
,
z
называется ортогональной составляющей
x.
при
этом y
называется ортогональной проекцией x
на
,
z
называется ортогональной составляющей
x.
Док-во:
ЛПП
и
таким образом оно также является
унитарным
(евклидовым) ( это ЛП : со скалярным
произведением из
)
в
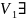 ОНБ. Пусть это Е={e1…eк}.
Тогда
ОНБ. Пусть это Е={e1…eк}.
Тогда
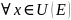 рассмотрим
рассмотрим
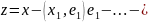 (
(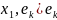 Поскольку
Поскольку
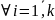
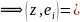 Из суммы
Из суммы
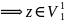
Таким
образом x=z+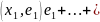 (
(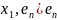 x=y+z,
x=y+z,
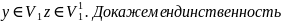 :
Пусть
:
Пусть