Вопрос 1

Опр. Система столбцов называется линейно зависимой, если нетривиальный набор 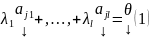. Если же (1) возможно только при , то система столбцов линейно независима.

Опр. Система строк называется линейно зависимой, если нетривиальный набор . Если же (2) возможно только при , то система строк линейно независима.

Достаточные условия о ЛЗ и ЛНЗ:

1. Система столбцов, содержащая нулевой столбец, линейно зависимая

# ЛЗ и ЛНЗ сохраняются при любой нумерации столбцов, поэтому БОО можно считать что ,

тогда =>это НТЛК =>ЛЗ #

2. Система столбцов, содержащая ЛЗ подсистему, ЛЗ

# БОО считаем линейно зависимая подсистема, :

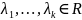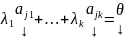=> это НТЛК => это ЛЗ#

3. Любая подсистема ЛНЗ системы столбцов является ЛНЗ

# Из предположения, что подсистема ЛЗ => система является ЛЗ, но по условию система столбцов является ЛНЗ => противоречие, значит подсистема ЛНЗ #

(Аналогично для системы строк)

Критерий ЛЗ

Система столбцов является ЛЗ  один из них является линейной комбинацией остальных.

• - ЛЗ система столбцов, 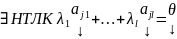, БОО

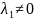
, т.е. - ЛК остальных

Пусть один из столбцов ЛК остальных БОО считаем Тогда

- это НТЛК=> линейно зависимая система

Вопрос 2

A=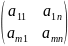 = 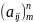– прямоугольная матрица

Опр. Минором k-ого порядка матрицы А (стоящего в строках 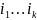и в столбцах 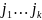) называется число:

Опр. Если , то по опр. ее ранг равен нулю. Если (Если ), то рангом ненулевой матрицы А называется

Опр. Пусть Rg A = r. Тогда любой ненулевой минор r-ого порядка этой матрицы называется базисным минором. Соответственно строки и столбцы, на пересечении которого расположен базисный минор, называется базисными строками и базисными столбцами.

Теорема о базисном миноре

1 Базисные строки/столбцы являются ЛНЗ

2 строка/столбец матрицы А является ЛК базисных строк/столбцов

Док-во:

1. # Пусть RgA=r. Пусть . Покажем что –ЛНЗ систем строк ( для столбцов аналогично) Пусть - ЛЗ. Тогда cтроки явл. ЛЗ=>одна из них является ЛК остальных=> По свойству det =0 – это противоречие => - ЛНЗ#

2. # Пусть – базисный минор матрицы А. Докажем для столбцов

Рассмотрим матрицу

B=

Если 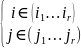, то det B=0 (т.к. есть одинаковые стр/столб)

Если , det B=0= (т.к. Rg A=r)

Т.е. в любом случае det B=0; разложим его по последней строке

0= , где – алгебраические дополнения последней строки, они одинаковы . Поэтому , причем (баз. минор)

Вопрос 3

Сл1. (Критерий вырожденности)

# Если А=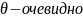

⇒. Пусть А вырожд. (т.е. det A=0). Единственный минор n-ого порядка матрицы A это M_n=detA=0

⇒Rg A=r – баз. минор=>ост.столбцы матрицы А явл-ся ЛК баз. столбцов => столбцы ЛЗ.

⇐. Столбцы ЛЗ⇒ один из них есть ЛК других ⇒detA=0#

Cл2. Если RgA=r, то любые (r+1) штука строк\столбецов будут ЛЗ, если они существуют

# для столбцов (от противного): пусть - ЛНЗ (предположение)

а) если r=m, тогда рассмотрим столбцы . Они ЛНЗ, т.к. являются подсистемой ЛНЗ системы⇒

любой столбец⇒

б)если m≥r+1, тогда рассмотрим

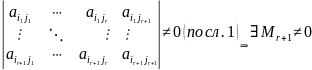
Т. (О ранге матрицы) RgA=max кол-ву ЛНЗ строк=max кол-ву ЛНЗ столбцов

#RgA=r⇒