Расчет прямозубых конических передач

1.2.Расчет конических закрытых прямозубых передач относительно среднего делительного диаметра шестерни

1.2.1.Определяем средний делительный диаметр шестерни из условия контактной прочности

d_m1 = 770

Т₁ – крутящий момент на валу шестерни, Н.м.

К_Hβ –коэффициент неравномерности распределения нагрузки по длине зуба, зависит оттвердости поверхности зубьев передачи и расположения колес относительно опор (табл. 1 )

Таблица 1

Коэффициент неравномерности распределения нагрузки

Расположение шестерни относительно опор	Твердость поверхности зубьев, НВ	Значения КНβ при ψвd
		0,2 ! 0,4 ! 0,6 ! 0,8
Консольное, опоры шарико- подшипники Консольное, опоры ролико- подшипники	≤ 350 >350 ≤ 350 > 350	1,08 1,17 1,28 - 1,22 1,44 - - 1,06 1,1 1,19 1,27 1,1 1,25 1,45 -

φ_bd - коэффициент ширины венца колеса по среднему делительному диаметру (табл.2 )

Таблица 2

Коэффициент ширины венца

Расположение шестерни относительно опор

Значения ψвd при твердости рабочей поверхности зубьев колеса НВ ≤ 350 ! НВ > 350

Консольное 0,3 – 0,4 0,2 – 0,25

[σ]_H – допускаемое контактное напряжение для материала колеса, как наиболее слабого звена передачи, Мпа

1.2.2.Находим ширину зубчатого венца колеса b = φ_bd·d_m1

1.2.3.Вычисляем внешний делительный диаметр шестерни и колеса

d_e1 = d_m1 + d₁·b/ u² + 1 , d_e2 = d_e1·u , уточняем по табл.3

Таблица 3

Ширина венца конического колеса (ГОСТ 12289-76)

Номинальный диаметр колеса, dе2 Значения в в мм. при номинальном передаточном числе 1,6 ! 1,8 ! 2,0 ! 2,24! 2,5 ! 2,8 ! 3,15 !3,55 ! 4,0 !4,0 ! 5,0
	125 140 160 180 200 225 250 280 315 355 400 500 560 630 710 800 900 1000	21 24 28 30 34 38 42 48 52 60 70 85 - - - - - -	20 22 26 30 32 36 40 45 52 60 65 80 90 100 120 130 - -	20 22 25 28 32 36 40 45 50 55 63 80 90 100 111 130 - -	19 21 25 28 30 36 40 45 50 55 63 80 90 100 110 125 140 160	19 21 25 28 30 34 38 42 48 55 60 75 85 95 110 125 140 150	19 21 24 28 30 34 38 42 48 55 60 75 85 95 110 120 140 150	19 21 24 26 30 34 38 42 48 55 60 75 85 95 105 120 130 150	19 21 24 26 30 34 38 42 48 52 60 75 85 95 105 120 130 150	18 21 24 26 30 32 36 42 45 52 60 75 80 90 105 120 130 150	- 20 24 26 30 32 36 40 45 52 60 75 80 90 105 120 130 150

1.2.4.Внешний окружной модуль передачи m_e = d_e1/Z₁ = d_e1/ (18 – 28), из найденного интервала величин выбираем одно стандартное значение (табл. 4). 1.2.5.Находим число зубьев шестерни и колеса

Z₂ = d_e2/m_e , Z₁ = Z₂/u ,вычисленные значения округляют до целых чисел.

1.2.6.Фактическое передаточное число u = Z₂/Z₁

1.2.7.Углы делительных конусов δ₁ = arctq 1/u , δ₂ = 90^ο –δ₁ .

1.2.8.Основные геометрические размеры передачи:

- внешние делительные диаметры шестерни и колеса

d_e1 = Z₁·m_e , d_e2 = Z_2··m_e

_- внешние диаметры вершин зубьев шестерни и колеса

d_ae1 = d_e1 + 2m_e·cos δ₁, d_ae2 = d_e2 + 2m_e·cos δ₂

- внешнее конусное расстояние R_e = Z_1·m_e/2 sinδ₁

_- среднее конусное расстояние R_m = R_e – 0,5в

- средний окружной модуль m = m_e -- в·sin δ₁/z₁, ( не округлчют)

- средние делительные диаметры шестерни и колеса

d_m1 = Z₁·m, d_m2 = Z₂·m

- высота головки зуба h_ae = m_e

_- высота ножки зуба h_fe = 1,2 m_e

_- угол ножки зуба, град. θ_f = arctq h_fe/R_е

1.2.9.Проверяем соблюдение условий

в/R_е< 0,285 , в< 10 m_е

Если условия не выполняются , рекомендуется уменьшить в.

1.2.10.Вычисляем окружную скорость колес и определяем степень точности изготовления колес (табл. 5)

Расчет закрытой прямозубой передачи по расчетному внешнему диаметру шестерни, мм

d_e1 = K_d

К_d = 101 МПа^1/3 – для прямозубых передач (β= 0),

К_be = b/R_e = 0,2 – 0,3 – коэффициент ширины зубчатого венца относительно внешнего конусного расстояния,

К_Hβ – коэффициент учитывающий неравномерность распределения нагрузки по ширине венца (табл. ),

К_A – коэффициент внешней динамической нагрузки (табл. ),

υ_H – коэффициент, учитывающий изменения прочности конической передачи по сравнению с цилиндрической, ( υ_H = 0,85)

1.3.2.Приняв Z¹₁ = 19, определяем модуль зацепления m^'_te = d^'_e1/Z^'₁ ,мм и округляют до ближайшей велечины в соответствии с ГОСТом (табл. ),

m_te = m_n ,мм.

1.3.3.Число зубьев шестерни Z₁ = d^'_e1/m_te. Число зубьев колеса Z₂ = Z_1·u.

(Z₁, Z₂ – целые числа ).

1.3.4.Фактическое передаточное число u_Ф = Z₂/Z₁

1.3.5.Углы делительных конусов, град.

δ₁ = arctq(Z_1/Z₂) ; δ₂ = arctq(Z₂/Z₁)

1.3.6.Внешние диаметры, мм

- делительные d_e1(2) = m_te·Z₁₍₂₎ ,

- вершин зубьев d_ae1(2) = d_e1(2) + 2m_te·cosδ₁₍₂₎ ,

- впадин зубьев d_f1(2) = d_e1(2) – 2,4m_te·cosδ₁₍₂₎

1.3.7.Внешнее конусное расстояние, мм. R_e = 0,5 m_teZ₁/2sinδ₁

1.3.8.Ширина венца зубчатых колес, мм b = R_e·K_be , b- целое число.

[m_te > (1/8 -:- 1/10)b]

1.3.9.Среднее конусное расстояние, мм.. R_m = R_e – 0,5b

1.3.10.Параметры колес в среднем сечении, мм

- средний модуль m_m = m_te·R_m/R_e. m = m_e – b sin(δ₁/Z₁)

- средние делительные диаметры d_m1(2) = m_m·Z₁₍₂₎

1.3.11. Высота головки и ножки зуба, мм

h_ae = m_e h_fe = 1,2m_e

1.3.12..Силы в зацеплении конических колес

- окружные силы, Н F_t1 = F_t2 =2 ·10³·T₁/d_m1 = 2· 10³·T₂/d_m2

• радиальные силы, Н F_r1 = F_t1·tqα·cosδ₁ ; F_r2 = F_t2·tqα·sinδ₁

• осевые силы, Н F_a1 = F_t1·tqα·sinδ₁ ; F_a2 = F_t2·tqα·cosδ₁

1.3.13. Расчет передачи на контактную прочность

σ_Н = Z_H·Z_E·Z_ε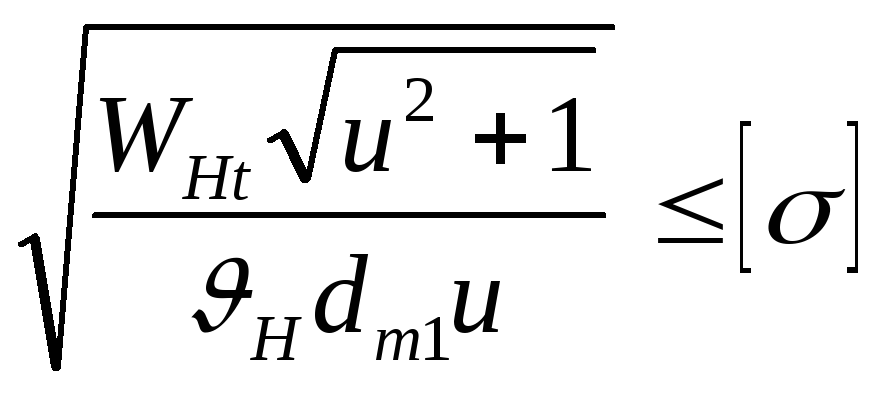

Z_H –коэффициент учитывающий форму сопряженных зубьев Z_H = 1,76

Z_E –коэффициент учитывающий механические свойства материалов сопряженных колес Z_E = 275 МПа^1/3

Z_ε – коэффициент учитывающий суммарную длину контактной линии Z_ε = 1,0

, где ε_α – коэффициент торцевого перекрытия зубьев

ε_α = [1,88 – 3,2( 1/Z_y1 ± 1/Z_y2)]

Z_y1, Z_y2 - эквивалентное число зубьев конической передачи

Z_y1 = Z₁/cosδ₁ Z_y2 = Z₂/cosδ₂

υ_Η – коэффициент учитывающий изменение прочности 0,85.

W_Ht – удельная расчетная окружная сила , Н/мм

W_Ht = F_t·K_Hα Κ_Ηβ Κ_Ηυ Κ_Α/b

Таблица

Значения коэффициента К_НV

Степень точности	Твердость поверхности зубьев	Окружная скорость υ, м/с 1 ! 2 ! 4 ! 6 ! 8 ! 10
7 8 9	≤ 350 350 ≤ 350 350 ≤ 350 > 350	1,94 1,07 1,14 1,21 1,29 1,36 1,08 1,05 1,09 1,14 1,19 1,24 1,04 1,08 1,16 1,24 1,32 1,40 1,03 1,06 1,10 1,16 1,22 1,26 1,05 1,10 1,20 1,30 1,40 1,50 1,04 1,07 1,13 1,20 1,26 1,32

По условию прочности расчетные контактные напряжения не должны превышать величину допускаемых для данного материала колеса [σ]_H2 .Разрешается отклонения в сторону перегрузки передачи не более 5%, а недогрузки не более 20%.

1.3.14. Расчетные напряжения изгиба в основании зуба конического колеса

σ_F1(2) = Y_FS1(2)·Y_β·Y_ε·W_Ft/υ_F·m_m<[σ]_F1(2)

σ_F = Y_FK_FβK_FV

Таблица: Значения коэффициента формы зуба Y_F

Zy YF Zy YF

17 4, 26 45 3,66

20 4,07 50 3,65

22 3,98 65 3,62

24 3,92 80 3,60

26 3,88 100 3,60

28 3,81 150 3,60

30 3,79 300 3,6

35 3,75

40 3,70

W_Ft = F_t·K_Fβ·K_Fν·K_FαK_A/b – удельная расчетная окружная сила при изгибе.

Y_FS1(2) – коэффициент формы зуба, зависит от эквивалентного числа зубьев конических колес (табл. )

Y_{β –}коэффициент, учитывающий наклон зуба

Для прямых зубьев Υ_β = 1,0 ; для косозубых Υ_β = 1 –β ^О/ 140 ^О ;

Y_ε –коэффициент, учитывающий перекрытие зубьев

Для прямых зубьев Υ_ε = 1,0 , для косых Υ_ε = 1 /ε_α ,где ε_α –коэффициент торцевого перекрытия : ε_{α =} [1,88- 3,2(1/Z₁ ±1/Z₂)]cosβ .

K_Fα –коэффициент, учитывающий неравномерность нагрузки для одновременно зацепляющихся зубьев:

• для прямых зубьев Κ_Fα =1,0; для косых зубьев табл.

Κ_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки,табл.

Или Κ_Fβ=1+1,5(Κ_Ηβ-1)

Таблица

Ориентировочные значения коэффициента К_Fβ

Расположение шестерни относительно опор	Твердость поверхностей зубьев колеса, НВ	ψвd = b/dm1 0,2 ! 0,4 ! 0,6 ! 0,8 ! 1,2 ! 1,6
Консольное, опоры шарико- подшипники Консольное, опоры ролико- подшипники	≤ 350 350 ≤ 350 > 350	1,16 1,37 1,64 - - - 1,33 1,70 - - - - 1,10 1,22 1,38 1,57 - - 1,20 1,44 1,71 - - -

Κ_Fν –коэффициент, учитывающий динамическую нагрузку, табл.

Таблица

Ориентировочное значение коэффициента К_FV

Cтепень точности	Твердость поверхности зубьев, НВ	Окружная скорость υ, м/с 1 ! 2 ! 4 ! 6 ! 8 ! 10
7	≤ 350 > 350	1,08 1,16 1,33 1,50 1,62 1,80 1,03 1,05 1,09 1,13 1,17 1,22
8	≤ 350 > 350	1,10 1,20 1,38 1,58 1,78 1,96 1,04 1,06 1,12 1,16 1,21 1,26
9	≤ 350 > 350	1,13 1,28 1,50 1,72 1,98 2,25 1,04 1,07 1,14 1,21 1,27 1,34

Расчет на изгиб выполняют для наиболее слабого звена конической передачи. Его выявляют из соотношения

для шестерни [σ_F1]/Y_F1 ; для колеса [σ_F2]/Y_F2

В расчетную формулу напряжений изгиба подставляют значения того звена, у которого выше указанное отношение меньше по величине

Если условия прочности на изгиб не выполняются т.е. σ_F > [σ_F] , следует увеличить модуль передачи m.