
- •Генеральная совокупность, понятие репрезентативности выборки из данных. Смещение выборки.
- •Частотные распределения. Разница между нормальным и равномерным распределением. Приведите пример визуализации графика распределения для своего набора данных.
- •Визуализация данных. Линейный график, столбчатые диаграммы, гистограммы, диаграммы рассеяния. Изобразить графически, описать суть графиков.
- •Меры вариативности. Перечислить основные типы (4), написать формулу для нахождения. Какие меры вариативности подвержены выбросам в данных? Подтвердите выводы на примере.
- •Влияние выбросов.
- •Меры центральной тенденции. Перечислить основные типы, написать формулу для нахождения. Какие меры вариативности подвержены выбросам в данных? Подтвердите выводы на примере.
- •Влияние выбросов.
- •Определение выброса в данных. Приведите примеры конвенций для определения верхней и нижней границы нормальных значений данных. Через iqr или sigma
- •Определение корреляции в данных. Свойства коэффициента корреляции. Формула для нахождения коэффициента корреляции.
- •. Сформулируйте центральную предельную теорему. Объясните её постулаты на практическом примере. Сформулируйте закон больших чисел.
- •Сформулируйте определения параметрических и непараметрических критериев при тестировании гипотез. Критерий согласия хи-квадрат. Определение и применение.
- •Критерий независимости хи-квадрат при тестировании гипотез. Для чего используется? Что такие таблица сопряженности?
- •Параметрические критерии. T-статистика. Напишите определение и формулу для вычисления. Понятие степеней свободы.
- •Одновыборочный и парный t-тест. Объяснить разницу. Придумать пример на тестирование гипотезы одним из тестов, вычислить t-наблюдаемое.
- •Простое сравнение для определения разницы:
- •Машина опорных векторов. Для решения каких задач применяется алгоритм? Объясните смысл алгоритма. Понятие гиперплоскости. Напишите наиболее распространенные ядерные функции.
- •Алгоритм knn. Для решения каких задач применяется алгоритм? Формула нахождения Евклидового расстояния. Опишите порядок действий при работе алгоритма.
- •Алгоритм Градиентного Бустинга. Для решения каких задач применяется алгоритм? Объясните принцип работы алгоритма. Основные параметры при работе алгоритма. Популярные реализации алгоритма.
Определение корреляции в данных. Свойства коэффициента корреляции. Формула для нахождения коэффициента корреляции.
Корреляция в статистике — это мера того, насколько сильно связаны две переменные. Если одна переменная изменяется, корреляция показывает, можно ли ожидать изменения в другой переменной, и какова величина этого изменения.
Свойства коэффициента корреляции:
Диапазон значений: Коэффициент корреляции может варьироваться от -1 до +1. Значение +1 -> увеличение одной переменной сопровождается увеличением другой. Значение -1 -> увеличение одной переменной сопровождается уменьшением другой.
Симметричность: Коэффициент корреляции между переменной X и переменной Y тот же, что и между Y и X.
Чувствительность к выбросам: Коэффициент корреляции может быть сильно искажен наличием выбросов.
Формула коэффициента корреляции Пирсона:
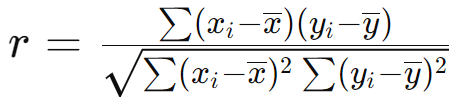
где:
и
 —
значения переменных X и Y,
—
значения переменных X и Y,
и
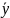 — средние значения X и Y соответственно.
— средние значения X и Y соответственно.
. Сформулируйте центральную предельную теорему. Объясните её постулаты на практическом примере. Сформулируйте закон больших чисел.
Центральная предельная теорема — это статистический принцип, который утверждает, что если брать достаточно большое количество независимых случайных величин из любого распределения с конечным средним и дисперсией, то распределение их средних значений будет приближаться к нормальному распределению, независимо от формы исходного распределения.
Пример: Измерение времени реакции. Представим, что вы проводите эксперимент, в котором разные люди должны нажать кнопку, как только увидят мигающий свет. Вы замеряете время реакции каждого человека.
Постулат 1: Независимость.
Каждый участник эксперимента реагирует на свет независимо от других. Время реакции одного человека не влияет на время реакции другого. Если один человек реагирует медленно, это не означает, что следующий тоже будет реагировать медленно.
Постулат 2: Идентичное распределение.
Все участники эксперимента реагируют в одинаковых условиях, и предполагается, что распределение времени их реакции будет одинаковым. Нет систематических различий в том, как тест проводится от одного человека к другому.
Постулат 3: Конечные среднее и дисперсия.
Время реакции людей имеет ограниченные минимальные и максимальные значения, то есть не может быть бесконечно большим или малым, и поэтому среднее время и разброс (дисперсия) этих времен тоже имеют конкретные, ограниченные значения.
Постулат 4: Достаточно большой объем выборки
Если вы измерите время реакции только у двух-трех человек, это не даст вам хорошего представления о времени реакции в целом. Но если вы измерите время реакции, например, у 50 или 100 человек, среднее из этих значений будет намного надежнее.
Закон больших чисел говорит нам, что чем больше раз вы повторяете эксперимент, тем ближе средний результат этих экспериментов будет к ожидаемому значению. Это ожидаемое значение — это то, что математически должно произойти на основе вероятности.
Допустим, у вас есть монета, она выпадает орлом и решкой с одинаковой вероятностью — по 50%. Если вы подбросите монету 10 раз, вы можете получить случайные результаты, например 7 раз орел и 3 раза решка. Если вы продолжите подбрасывать монету, скажем, 1000 раз, то количество выпадений орла и решки будет всё ближе и ближе к равному распределению (500 орлов и 500 решек из 1000).
Разделение выборки на обучающую и валидационную. Какое отношение данных обучающей выборки к валидационной обычно используется, для чего используются выборки? Опишите процесс стратификации данных, объясните для чего он используется.
Разделение данных на обучающую и валидационную предназначены для оценки производительности моделей на новых, ранее не виденных данных.
80/20: Это одно из наиболее часто используемых соотношений, где 80% данных идет на обучение, а 20% — на валидацию.
Обучающая выборка: Используется для тренировки модели, то есть для настройки параметров и обучения алгоритма на основе известных выходных данных.
Валидационная выборка: Используется для проверки эффективности модели. Данные из валидационной выборки не используются в процессе обучения. Это позволяет оценить, как модель будет работать на новых данных, что помогает избежать переобучения.
Процесс стратификации предполагает разделение данных таким образом, чтобы в каждой из выборок (обучающей и валидационной) сохранилось примерно одинаковое распределение ключевых переменных или классов.
Пример стратификации:
Допустим, у нас есть исследование по изучению эффективности лекарства с участием 1000 пациентов. Демографические данные показывают, что 600 мужчин и 400 женщин. Важно сохранить эту пропорцию при разделении данных:
Шаг 1: Выбираем пол как ключевую переменную для стратификации.
Шаг 2: Формируем две страты: одна для мужчин, другая для женщин.
Шаг 3: Если мы разделяем данные на 80% для обучения и 20% для валидации, то из страты мужчин 480 (80% от 600) попадут в обучающую выборку, а 120 в валидационную. Из страты женщин 320 попадут в обучающую выборку, а 80 в валидационную.
Постановка и тестирование гипотез. Что такое нулевая и альтернативная гипотеза? Виды альтернативных гипотез. Что такое уровень статистической значимости α? Определение критической области. Ошибка первого и второго рода.
Нулевая гипотеза предполагает отсутствие эффекта или различия. Например, если мы исследуем влияние нового лекарства на давление, нулевая гипотеза будет утверждать, что лекарство не имеет эффекта на давление.
 Альтернативная
гипотеза
предполагает наличие наблюдаемого
эффекта, различия или взаимосвязи. В
примере с лекарством альтернативная
гипотеза будет утверждать, что лекарство
влияет на давление.
Альтернативная
гипотеза
предполагает наличие наблюдаемого
эффекта, различия или взаимосвязи. В
примере с лекарством альтернативная
гипотеза будет утверждать, что лекарство
влияет на давление.
Двусторонняя альтернативная гипотеза. Исследуемый эффект может проявляться в любом направлении (может быть как положительным, так и отрицательным). Вы не уточняете, как именно изменится результат, только что он изменится.
Односторонняя альтернативная гипотеза предполагает, что изменения произойдут только в одном, заранее определенном направлении.
Уровень статистической значимости — это пороговое значение, которое мы выбираем, чтобы решить, когда результаты нашего эксперимента достаточно убедительны, чтобы сказать, что новое лекарство действительно работает. Выбираем α=0.05. Это означает, что вы готовы принять до 5% вероятности того, что вы ошибочно решите, что лекарство эффективно, когда на самом деле это не так.
Критическая область — это диапазон значений, которые считаются "слишком экстремальными", чтобы быть результатом случайности, если нулевая гипотеза верна. Если результат вашего анализа попадает в диапазон, который происходит реже, чем в 5% случаев (когда нулевая гипотеза верна), то это значение находится в критической области .критическая область помогает вам решить, когда результаты эксперимента достаточно убедительны, чтобы заключить, что лекарство работает, исходя из того, какой уровень уверенности (α) вы изначально установили.
Ошибка первого рода происходит, когда вы отвергаете нулевую гипотезу, хотя она на самом деле верна. В контексте нашего примера это означает, что вы решаете, что лекарство эффективно снижает давление, когда на самом деле это не так. (ложно отрицательный результат).
Ошибка второго рода происходит, когда вы не отвергаете нулевую гипотезу, хотя на самом деле она неверна. В нашем примере это будет значить, что вы решаете, что лекарство не эффективно (то есть оставляете нулевую гипотезу в силе), когда на самом деле оно эффективно. (ложно положительный результат).
Метрики качества моделей машинного обучения. Изобразите матрицу ошибок для бинарной классификации. Напишите формулу для вычисления True Positive Rate и False Negative Rate. Метрика Accuracy. В каких случаях её применение даёт ложный результат о качестве модели? Что такое ROC-кривая. Что такое AUC ROC.
Матрица ошибок — это таблица, которая позволяет визуализировать производительность алгоритма классификации.
-
Предсказано Positive
Предсказано Negative
Actual Positive
True Positive
False Negative
Actual Negative
False Positive
True Negative
True Positive (TP): Количество правильно идентифицированных положительных случаев.
False Negative (FN): Количество положительных случаев, ошибочно классифицированных как отрицательные.
False Positive (FP): Количество отрицательных случаев, ошибочно классифицированных как положительные.
True Negative (TN): Количество правильно идентифицированных отрицательных случаев.
True
Positive
Rate
(TPR)
измеряет способность модели правильно
идентифицировать положительные случаи.
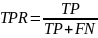
False Negative Rate (FNR)
показывает, какая доля из всех положительных
случаев была пропущена.
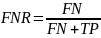
Accuracy
измеряет долю правильных предсказаний
(как положительных, так и отрицательных)
от всех предсказаний. Accuracy
=
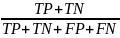
Accuracy не различает между классами: она просто подсчитывает общее количество правильных предсказаний. В случае с несбалансированными классами большинство данных принадлежит к одному классу, и модель может достичь высокой точности, просто всегда предсказывая наиболее часто встречающийся класс.
ROC-кривая - график, который показывает, как хорошо модель машинного обучения может различать два класса (например, больные vs здоровые) при разных пороговых значениях классификации. Ось X (False Positive Rate, FPR), Ось Y (True Positive Rate)
AUC (Area Under the Curve) ROC — это площадь под ROC-кривой. Численная мера, которая агрегирует информацию с ROC-кривой в одно значение, позволяющее легко сравнивать разные модели.
