Влияние выбросов.

Среднее значение наиболее подвержено влиянию выбросов, так как оно учитывает все значения в наборе данных. В то время как медиана и мода устойчивы к выбросам.

Рассмотрим набор данных: 3,5,7,9,11,100. Здесь 100 — выброс.

Среднее значение без выброса: (3+5+7+9+11)/5=7

Среднее значение с выбросом: (3+5+7+9+11+100)/6≈22.5

Медиана без выброса: 7

Медиана с выбросом: 8 (среднее между 7 и 9)

Мода: Не определяется в обоих случаях, так как все значения уникальны.

7. Стандартизированное распределение (z-распределение) и его свойства. Для чего используется? Напишите формулу для нахождения z-оценки. Придумайте пример для нахождения стандартизированного распределения, визуализируйте полученный результат

Z-распределение – это математическая модель, которая описывает распределение значений, которые были преобразованы таким образом, что их среднее значение (µ) становится равным 0, а стандартное отклонение (σ) — равным 1.

Свойства:

• Среднее значение (µ) z-распределения равно 0.

• Стандартное отклонение (σ) z-распределения равно 1.

• Форма z-распределения — это стандартное нормальное распределение, т.е. колоколообразная кривая

Использование:

• Для сравнения разных наборов данных. В одной школе оценки выставляются по 100-балльной шкале, а в другой — по 10-балльной. Прямое сравнение оценок будет некорректным из-за разницы в шкалах. Преобразование оценок в Z-распределение поможет стандартизировать их, т.е. привести к общей шкале, где средний балл становится 0, а стандартное отклонение — 1.

• Для определения, насколько далеко конкретное значение отклоняется от "нормы". например, если рост человека в Z-распределении равен 2, это означает, что его рост на два стандартных отклонения выше среднего — такой рост встречается довольно редко. Позволяет быстро оценить, насколько значения отличаются от ожидаемых или типичных.

Формула: 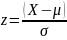, где X – значение из набора данных, – среднее значение из набора данных, σ — стандартное отклонение набора данных.

П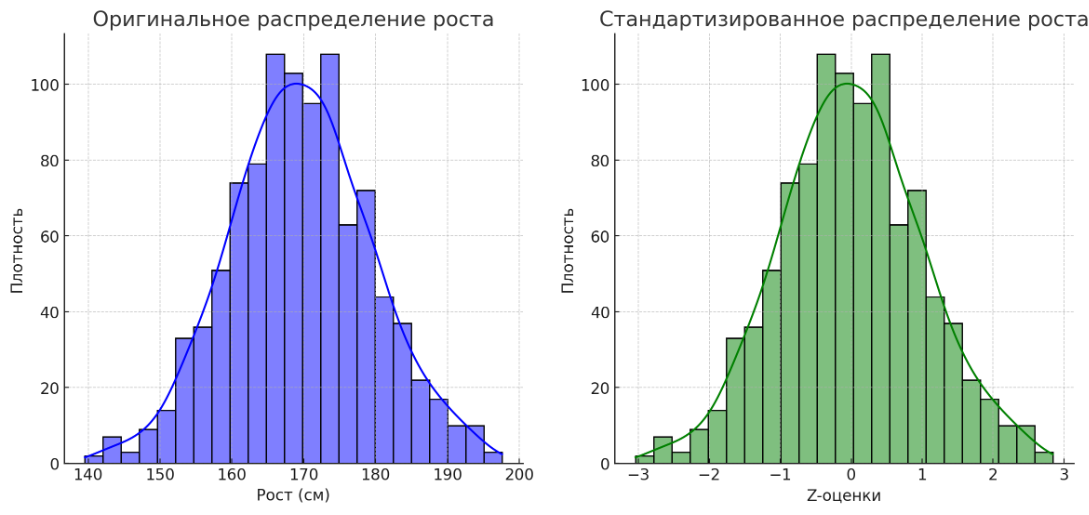 ример: Предположим, у нас есть данные о росте группы из 1000 человек. Средний рост составляет 170 см с стандартным отклонением 10 см. Мы хотим найти z-оценку для человека ростом 190 см.

= 2 => Рост 190 см находится на 2 стандартных отклонения выше среднего.

8. Определение выброса в данных. Приведите примеры конвенций для определения верхней и нижней границы нормальных значений данных. Через iqr или sigma

Выбросы в данных — это аномальные значения, которые значительно отличаются от большинства других значений в наборе данных.

Определение выбросов через IQR (межквартильный размах).

IQR равен разнице между третьим квартилем (Q3) и первым квартилем (Q1) данных

Значения, которые выходят за эти границы, считаются выбросами. Иногда используют множитель 3 вместо 1.5 для более консервативного определения выбросов, что помогает исключить только самые экстремальные случаи.

Конвенции для определения границ:

• Нижняя граница: Q1−1.5×IQR

• Верхняя граница: Q3+1.5×IQR

Пример: данные о возрасте [22, 23, 24, 22, 56, 24, 25, 23, 21, 22, 55].

Q1 (25-й перцентиль): 22

Q3 (75-й перцентиль): 25

IQR = 25 - 22 = 3

Нижняя граница = 22 - 1.5*3 = 17.5

Верхняя граница = 25 + 1.5*3 = 29.5

Значения 56 и 55 считаются выбросами, так как они выше верхней границы.

Определение выбросов через sigma (стандартное отклонение)

Где μ — среднее значение, σ — стандартное отклонение, а k — коэффициент, который чаще всего равен 2 или 3. При k=2 охватывается примерно 95% данных, а при k=3 — около 99%.

Конвенции для определения границ:

• Нижняя граница: μ−k×σ

• Верхняя граница: μ+k×σ

Пример: данные о возрасте [22, 23, 24, 22, 56, 24, 25, 23, 21, 22, 55].

Предположим, что среднее значение тех же данных равно 30, а стандартное отклонение — 10.

Нижняя граница при k=2: 30 - 2*10 = 10

Верхняя граница при k=2: 30 + 2*10 = 50

Значения вне этого диапазона считаются выбросами.

9. Стратегии работы с пропущенными значениями в данных. Приведите примеры действий для разных данных (заполнение средним значением, медианой, использование вектора значений, удаление столбцов с данными)

1. Удаление записей. Этот метод подходит, если пропущенных данных немного, чтобы это не повлияло на объем и представительность вашего набора данных.

2. Заполнение средним значением. Пропущенные значения можно заполнить средним значением по столбцу. Этот метод подходит для числовых данных с нормальным распределением.

3. Заполнение медианой. Для данных, которые могут содержать выбросы или не распределены нормально, лучше использовать медиану.

4. Заполнение модой. Моду можно использовать для заполнения пропущенных значений в категориальных данных.

5. Импутация константой. Пропущенные значения заполняются фиксированным значением, которое не встречается среди других значений данных, например, 0 или -1, что позволяет легко идентифицировать импутированные значения.

6. Предсказание пропущенных значений. : Использование моделей машинного обучения для предсказания пропущенных значений на основе других данных в наборе.

7. Интерполяция. Метод, особенно полезный во временных рядах, где пропущенные значения могут быть заполнены, используя значения, которые идут до и после пропуска. (В данных о ежедневной температуре можно интерполировать пропущенные значения, используя среднее между значениями предыдущего и следующего дней.)