Классификация признаков данных: (Качественные и количественные, непрерывные и дискретные). Номинальные, порядковые, интервальные, дихотомические, относительные переменные. Объяснить суть + примеры
Качественные признаки описывают категории или группы. Эти данные обычно текстовые или символьные. Пример: Цвет автомобиля (красный, синий, зеленый).
Количественные признаки представляют собой числовые данные, которые можно измерить. Пример: Вес человека (70 кг, 80 кг).
Непрерывные признаки могут принимать любое значение в заданном диапазоне. Пример: Температура воздуха может быть 22.5, 22.6, 22.7 градусов и т.д.
Дискретные признаки принимают только определенные, изолированные значения. Пример: Количество детей в семье (1, 2, 3).
Номинальные переменные — это категориальные данные без определенного порядка. Пример: цвет глаз (карие, зеленые, голубые, серые)
Порядковые переменные имеют естественный порядок, но без равного расстояния между значениями. Пример: Уровень образования (начальное, среднее, высшее).
Интервальные переменные имеют как порядок, так и равное расстояние между значениями, но без абсолютного нуля. Пример: Температура по Цельсию.
Относительные переменные измеряются относительно какой-то базы, имеют ноль и описывают соотношения. Пример: доля женщин в общем числе сотрудников в компании.
Дихотомические переменные — или бинарные, это специальный тип номинальных переменных, которые принимают только два возможных значения. Пример: Пол (мужской, женский).
Генеральная совокупность, понятие репрезентативности выборки из данных. Смещение выборки.
Генеральная совокупность — это полный набор всех элементов или событий, которые мы хотим изучить. Это может быть всё население страны, все продукты на складе, все транзакции за год и т.д. Генеральная совокупность включает в себя все возможные объекты исследования, которые соответствуют определенным критериям.
Репрезентативная выборка — это такая подгруппа генеральной совокупности, которая точно отражает характеристики всей совокупности. Репрезентативность важна, потому что она обеспечивает то, что выводы, сделанные на основе выборки, могут быть корректно распространены на всю генеральную совокупность. Чтобы выборка была репрезентативной, она должна быть выбрана методом случайной выборки, где каждый элемент генеральной совокупности имеет равные шансы быть включенным в выборку.
Пример: Представим, что мы хотим исследовать здоровье населения страны. Генеральная совокупность здесь — все жители страны. Репрезентативная выборка должна включать людей всех возрастных групп, полов, экономических статусов и регионов страны в таких пропорциях, каковы они в реальности.
Смещение выборки — это искажение в данных, которое возникает, когда выбранная выборка не адекватно отражает общую генеральную совокупность. Результаты, полученные на основе такой выборки, не будут точно передавать характеристики или мнения всей генеральной совокупности. В результате такого смещения выводы исследования могут быть неверными или искаженными.
Частотные распределения. Разница между нормальным и равномерным распределением. Приведите пример визуализации графика распределения для своего набора данных.
Частотное распределение — это метод организации данных, который показывает, как часто каждое значение встречается в наборе данных. Это можно представить в виде таблицы или графика, и это помогает анализировать данные. Часто частотное распределение визуализируется с помощью гистограммы.
Нормальное распределение (или Гауссово распределение) — это вероятностное распределение, где большинство значений сгруппированы вокруг среднего значения, и они убывают симметрично в обе стороны. График нормального распределения имеет форму колокола и симметричен относительно среднего значения.
Это распределение характеризуется двумя параметрами: средним значением (µ) и стандартным отклонением (σ). Примеры: Рост людей, давление, ошибки измерений и другие природные и социальные явления, которые подвержены множеству мелких случайных воздействий.
Равномерное распределение, в отличие от нормального, не имеет выраженного "центра". Все значения в заданном диапазоне встречаются с равной вероятностью. Определяется минимальным и максимальным значениями (a и b). Все значения между этими точками равновероятны. Примеры: идеально случайный выбор числа от 1 до 6 на игральной кости, случайный выбор страницы в книге.
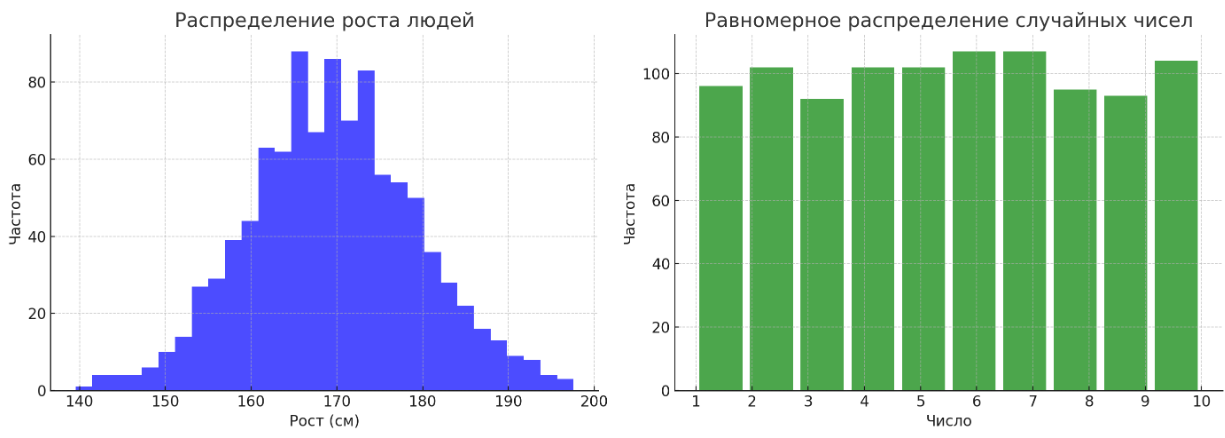
Пример визуализации графика
Слева: нормальное распределение роста людей
Справа: равномерное распределение Случайных чисел
