7. Материалы червяков и венцов червячных колес.

Червяк и колесо должны обладать достаточной прочностью и ввиду значительных скоростей скольжения в зацеплении образовывать антифрикционную хорошо прирабатываемую пару.

Червяки изготавливают из среднеуглеродистых сталей марок 45, 50 или легированных 40Х, 40ХН с поверхностной или объемной закалкой до твердости 45 …54 НRC и последующим шлифованием витков Хорошо работают передачи из цементуемых сталей 18ХГТ, 20Х с твердостью после закалки 56 …63 НRC.

Материалы зубчатых венцов червячных колес по мере убывания анти- задирных и антифрикционных свойств и рекомендуемым для применения скоростям скольжения условно делятся:

1. Оловянные бронзы (БрО10Ф1, БрО10Н1Ф1…) – применяют при высоких скоростях скольжения (до 5 …25 м/с).Обладают хорошими антифрикционными свойствами, но невысокой прочностью.

2. Безоловянные бронзы и латуни – применяют при средних скоростях скольжения (до 3…5 м/с). Пример – БрА9Ж3Л – высокая механическая прочность, но пониженные анти задирные свойства.

3. Серые чугуны марок СЧ15, СЧ20 применяют при малых скоростях скольжения (до 2 …3м/с) в механизмах с ручным приводом.

Для выбора материала колеса предварительно определяют ожидаемую скорость скольжения, м/с :ν_ск = 0,45· 10^-3·n₁·

8. Характер и причины отказов червячных передач

• усталостное выкрашивание рабочих поверхностей – причина – контактные напряжения превышающие предел выносливости материала (оловянные бронзы);

• заедание – из за значительных скоростей скольжения Применять противоизносные и противозадирные присадки с маслами И-Г-С-220, И-Т-С-320, И-Т-Д-100.

• изнашивание зубьев колес – обусловленно заеданием рабочих поверхностей червячной пары. Увеличивается зазор в зацеплении.

• излом зубьев червячных колес – после изнашивания.

Для предупреждения заедания, изнашивания рекомендуется тщательно обрабатывать поверхности витков и зубьев, применять материалы с высокими антифрикационными свойствами, а масла с противоизносными и противозадирными свойствами.

9. Расчет передач на контактную прочность и предотвращение заедания.

Расчет по контактным напряжениям является основным, а расчеты на предотвращение заедания и по напряжениям изгиба – проверочными.

Наибольшее контактное напряжение определяют по формуле Герца:

Силу действующую по нормали в точке контакта зуба червячного колеса и витка червяка F_n, определяют по окружной силе F_t2 c учетом угла наклона зуба колеса г_w и коэффициента нагрузки К: F_n = K F_t2/(cosα cosγ _w),

где К = К_НV К_Нв - учитывает внутреннюю динамику передачи и неравномерность распределения нагрузки в зоне контакта вследствие

деформации валов червяка и колеса, подшипников и корпуса.

Под b в формуле Герца понимают суммарную длину контактной линии в зацеплении червячной передачи: b = рd_w12д/360⁰. Если учесть, что с увеличением угла γ подъема витка длина линии контакта растет обратно пропорционально cosγ _w то при коэффициенте торцевого перекрытия ε_α в средней плоскости червячного колеса и коэффициенте колебания суммарной длины контактных линии получим:

При средних значениях ζ = 0,75,угла обхвата 2δ = 100 и коэффициенте ε = 2

Суммарная длина контактных линий равна:

Радиус кривизны профиля зуба червячного колеса в полюсе зацепления с учетом угла наклона зуба γ:

Тогда

Для сочетания сталь – бронза или сталь – чугун имеем модуль упругости Е₁ = 2,1 10⁵МПа , Е₂ = (0,9…1,0) 10⁵МПа, ν₁= 0,3, ν₂= 0,25…0,33 , примем α = 20 ; γ = 10 . Проведем подстановку в формулу заменив при этом значения:

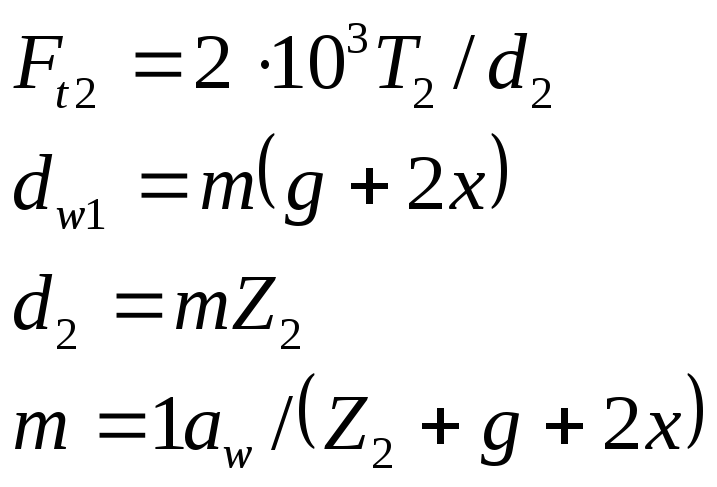
то получим формулу проверочного расчета червячных передач по контактным напряжениям:

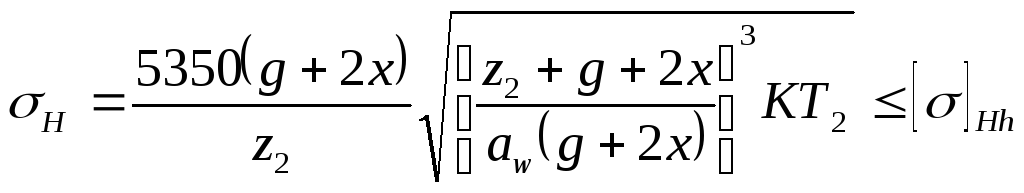
σ_Н, [σ]_Н в МПа; а_W в мм; Т₂ в Н.м.

Червячные передачи с нелинейными червяками характеризует более благоприятное соотношение радиусов кривизны, а так же большая суммарная длина контактной линии, что обуславливает их повышенную нагрузочную способность. Расчет аналогичный с заменой числового коэффициента 5350 на 4340.

В упрощенных расчетах предотвращение заедания обеспечивают выбором допускаемых контактных напряжений.

10. Расчет зубьев колес на прочность при изгибе.

Расчет производим для зубьев червячного колеса:

Y_F2 – коэффициент формы зуба колеса, который выбирают в зависимости от эквивалентного числа зубьев (большее значение коэффициента соответствует меньшему значению чисел зубьев:

Z_v2 = Z₂/

11.Выбор допускаемых напряжений.

Допускаемые контактные напряжения:

1 группа. Для оловянистых бронз (БрО10Н1Ф1, БрО10Ф1, …) [σ]_Н определяют из условия сопротивления усталостному выкрашиванию рабочих поверхностей зубьев:

[σ]_Н = σ^о_Н· С_v· К_НL,

где σ_Н^о – предел контактной выносливости при числе циклов перемены напряжений 10⁷, σ_Н^о = (0,75…0,9)σ_{В ;} σ_{В –временное сопротивление для бронзы на растяжение}

С_v – коэффициент, учитывающий интенсивность изнашивания зуба колеса в зависимости от скорости скольжения (график );

К_НL – Коэффициент долговечности, К_НL

2.группа. [σ]_Н – для безоловянных бронз и латуней (БрА9Ж3Л, ЛЦ23А6Ж3Мц2 ….) определяют из условия сопротивления заеданию:

[σ]_Н = (250 …300) – 25V_ск ,

3.группа. Для чугунов (СЧ15, СЧ20, …) [σ]_{Н –} определяют из условия сопротивления заеданию: [σ]_Н = (175 …200) – V_ск

Допускаемые напряжения изгиба:

Для зубьев червячного колеса зависят от материала, требуемого ресурса и характера нагрузки. Для бронзовых венцов червячных колес при нереверсивной передаче (работа зубьев одной стороной) допускаемые напряжения изгиба [σ]_F = σ_F^о· К_FL,

где σ_F^о- предел изгибной выносливости при числе циклов перемены напряжений 10⁶,

σ _F^о= 0,08σ_в+ 0,25σ_т, здесь σ_т,, σ_В - соответственно предел текучести, временное сопротивление бронзы при растяжении.

К_FL= 25· 10⁷ – коэффициент долговечности.

Для чугунных червячных колес при работе зубьев одной стороной: [σ]_F = 0,22σ_ви,

где σ_ви – предел прочности при изгибе, МПа (обычно в 1,5 …2,2 раза больше временного сопротивления при растяжении σ_В)