Министерство образования Республики Беларусь

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра экономической информатики

Практическая работа №2

«Метрики сложности потока управления программ.»

Вариант 17

Выполнил:	студент группы
Проверил:	Старший преподаватель кафедры ПОИТ Грибович А. А.

Минск 2024

СОДЕРЖАНИЕ

ХОД ПРАКТИЧЕСКОЙ РАБОТЫ 3

1. Исходные предоставленные данные 3

2. Детализированная схема алгоритма по ГОСТ 19. 701-90 3

3. Расчёт метрики Маккейба и определение базисных независимых путей 5

4. Расчёт метрики Джилба 5

5. Расчет метрики граничных значений 6

6. Результаты расчётов метрик в виде итоговой таблицы 7

ХОД ПРАКТИЧЕСКОЙ РАБОТЫ

Цель работы: на основе разработанной в ПР 1 детализированной схемы алгоритма, представленной в соответствии с положениями ГОСТ 19701-90, рассчитать метрики сложности потока управления программ (метрики Маккейба, Джилба, максимальный уровень вложенности условного оператора, метрику граничных значений). 

1. Исходные предоставленные данные

Для значений Х, изменяющихся от –1,5 до 2 с шагом 0,01, вычислить значения функции Y: 

Рисунок 1.1 – Вариант индивидуального задания

Полученные значения Y занести в массив. Вывести значения Х и соответствующие им значения элементов результирующего массива.

2. Детализированная схема алгоритма по ГОСТ 19. 701-90

Схема – это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени – чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз.

Рисунок 2.1 – Блок-схема алгоритма

3. Расчёт метрики Маккейба и определение базисных независимых путей

Метрика Маккейба предназначена для оценки трудоемкости тестирования программы. Данная метрика определяется по формуле:

Z(G) = e – ʋ + 2p,

где е — число дуг ориентированного графа G; ʋ — число вершин; р — число компонентов связности графа.

Число дуг: e = 20.

Число вершин: ʋ = 17, p = 1.

Цикломатическое число Маккейба равно:

Z(G) = 20-17+2*1 = 5.

Значение метрики Маккейба показывает, что в схеме алгоритма можно

выделить 5 базисных независимых путей.

Таким образом, для тестирования совокупности базисных независимых

путей исследуемой программы необходимо выполнить минимально 5

тестовых прогонов.

1-й путь. 1-2-3-4-5-6(нет)-13-14(нет)-17

2-й путь. 1-2-3-4-5-6(нет)-13-14(да)-15-16-14(нет)-17

3-й путь. 1-2-3-4-5-6(да)-10(да)-9-6(нет)-13-14(нет)-17

4. Расчёт метрики Джилба

Данная метрика определяет логическую сложность программы как насыщенность ее условными операторами IF–THEN–ELSE.

CL – количество условных операторов, характеризующее абсолютную сложность программы;

сl – насыщенность программы условными операторами, характеризующая относительную сложность программы;

cl определяется как отношение CL к общему количеству операторов программы.

CL = 4;

cl = 4/(17 - 2 - 4) = 0.36 (количество операторов программы равно 11, поскольку блоки ввода-вывода, а также блоки «начало» и «конец», используемые при вычислении метрики Маккейба, не принимаются во внимание при вычислении метрики Джилба)

Максимальный уровень вложенности условного оператора CLI = 3.

5. Расчет метрики граничных значений

Таблица 1 – Свойства подграфов программы.

Свойства подграфов программы	Номер вершины выбора
	6	7	10	14
Номера вершин перехода	7, 13	8, 10	11, 12	15, 17
Скорректированная сложность вершины выбора	8	5	4	4
Номера вершин подграфа	6-12	8,10,11,12	10-12	14-16
Номер нижней границы подграфа	13	9	9	17

Таблица 2 – Скорректированные сложности вершин графа программы

Номер вершины графа программы	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Скорректированная сложность вершины графа	1	1	1	1	1	8	7	1	1	4	1	1	1	4	1	1	1
Sa = 34

Относительная граничная сложность программы S_o определяется по формуле:

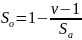
0,53

6. Результаты расчётов метрик в виде итоговой таблицы

Таблица 3 – Итоговая таблица

Метрики сложности потока управления программ	Значения
Метрика Маккейба, Z(G)	5
Абсолютная сложность программы CL по метрике Джилба	4
Относительная сложность программы cl по метрике Джилба	0,(36)
Максимальный уровень вложенности условного оператора CLI по метрике Джилба	3
Метрика граничных значений (абсолютная граничная сложность программы) Sa	34
Метрика граничных значений (относительная граничная сложность программы) S0	0,53