31. Сложение гармонических колебаний

 Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.

Сложение двух колебаний одного направления (сонаправленных колебаний)

 

можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.

На Рисунке 2.1 показаны векторы амплитуд А₁(t) и А₂(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны   и  . Сложение колебаний сводится к определению  . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.

Результирующему колебанию   соответствует на векторной диаграмме вектор амплитуды   и фаза  .

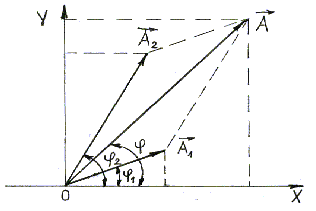
Рисунок 2.1 – Сложение сонаправленных колебаний.

Величина вектора А(t) может быть найдена по теореме косинусов:

.

Фаза результирующего колебания задается формулой:

.

Если частоты складываемых колебаний ω₁ и ω₂ не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.

 Сложение взаимно перпендикулярных колебаний

1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.

Рисунок 2.3

Складываемые колебания имеют вид:

  .

Частоты колебаний определяются как  ,  , где  ,   -коэффициенты жесткости пружин.

32. Физический и математический маятник(малые колебания без затухания)

Математический маятник представляет собой материальную точку, подвешенную на невесомой и нерастяжимой нити.

В соответствии с динамическим уравнением вращательного движения

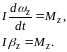
Для рассматриваемой системы

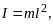
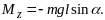
Следовательно уравнение движения имеет вид:

Для малых углов

Введя обозначение получим

Решением этого уравнения является функция кинематическое уравнение гармонических колебаний математического маятника.

Период этих колебаний

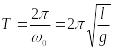
Частота

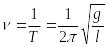
Физический маятник представляет собой твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси, не проходящей через центр тяжести тела. (Колебания совершаться не будут).

Уравнение колебаний физического маятника аналогично уравнению математического маятника и запишется в виде

Где

Период колебаний физического маятника определяется формулой

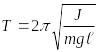
Математический маятник с приведённой длиной 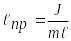будет иметь такой же период колебаний, как и данный физический. При этом точка будет центром качания физического маятника.

33. Затухающие колебания. Уравнение затухающих колебаний и его решение.

Свободные колебания — это колебания, происходящие в системе, предоставленной самой себе, после выведения ее из состояния равновесия. Свободные колебания могут быть гармоническими и затухающими.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени.

Динамическое уравнение затухающих колебаний

При наличии сопротивления ускорение материальной точки, совершающей колебания, обусловлено действием двух сил: возвращающей (квазиупругой) и силы сопротивления.

По второму закону Ньютона:

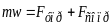
В проекциях на ось ОХ:

Разделим обе части этого уравнения на т, и введем обозначения

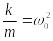
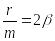
Получим дифференциальное уравнение затухающих колебаний:

Кинематическое уравнение затухающих колебаний

Решением данного дифференциального уравнения является функция

-циклическая частота затухающих колебаний;

- коэффициент затухания – величина, характеризующая быстроту затухания.