25. Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси.

26. Кинетическая энергия вращающегося твердого тела. Работа внешних сил при вращении твердого тела.

27. Гироскоп. Гироскопический эффект. Прецессия гироскопа.

Гироскопом называют массивное симметричное тело, вращающееся с большой угловой скоростью вокруг оси симметрии. Поскольку ось гироскопа совпадает с одной из главных осей инерции, то

где I — момент инерции гироскопа относительно этой оси; ω — угловая скорость собственного вращения.

Гироскопический эффект — способность быстро вращающегося тела удерживать своё положение в пространстве в плоскости своего вращения.

Прецессия гироскопа — такой тип движения, когда в результате постоянного действия момента внешней силы ось свободного гироскопа вращается вокруг направления данной внешней силы.

28. Уравнения динамики твердого тела, совершающего плоское движение. Кинетическая энергия твердого тела при плоском движении.

Уравнение динамики плоского движения относительно оси, проходящей через центр масс тела и неподвижной относительно тела, определяющее угловую скорость w_c вращательного движения: I_cdw_c/dt=^внешн.M_c, где I_c и ^внешн.M_c – момент инерции тела и момент внешних сил относительно этой оси соответственно.

Кинетическая энергия тела, совершающего плоское движение. Если рассматривать движение тела как вращение вокруг мгновенной оси, то элемент массы  m_i имеет в данный момент времени линейную корость v_i = wr_i , где r_i – расстояние от этого элемента до мгновенной оси. Кинетическая энергия отдельного элемента тела будет:

E_ki= m_iv²_i= mir2iw2, а кинетическая энергия всего тела: E_k=(сумм)  E_ki=w²/2(сумм)  m_ir²_i=Iw²/2, где I – момент инерции тела относительно мгновенной оси.

29. Уравнение свободных колебаний под действием квазиупругой силы и его общее решение

Свободные колебания — это колебания, происходящие в системе, предоставленной самой себе, после выведения ее из состояния равновесия. Свободные колебания могут быть гармоническими и затухающими.

Гармонические колебания – это периодические колебания, происходящие по гармоническому закону косинуса или синуса под действием квазиупругих сил.

Квазиупругие силы – силы, пропорциональные смещению и стремящиеся вернуть систему в положение равновесия.

Преобразуем уравнение

Введем обозначение

Динамическое уравнение приобретает вид:

Решением динамического уравнения является функция

А – амплитуда колебания,

- циклическая частота ,

- фаза колебания,

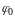- начальная фаза колебания .

30. Гармонический осциллятор. Энергия гармонического осциллятора.

 Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д.

В классической механике, гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы  , пропорциональной смещению   (согласно закону Гука):

где   — положительная конс танта, описывающая жёсткость системы.

Смещение колеблющейся точки от положения равновесия, описывается уравнением:

ее ускорение равно второй производной от смещения по времени

тогда сила, действующая на колеблющуюся точку, по второму закону Ньютона равна

- то есть сила пропорциональна смещению х и направлена против смещения к положению равновесия. Эта сила называется возвращающей силой.

Возвращающей силой в случае:

- груза на пружине является сила упругости,

- математического маятника – составляющая силы тяжести.

Возвращающая сила по характеру подчиняется закону Гука F= -kx,

где  – коэффициент возвращающей силы.

Тогда потенциальная энергия колеблющейся точки равна:

(постоянную интегрирования выбирают равной нулю, чтобы при х=0 энергия Wn=0).

_{Кинетическая энергия осциллятора:}

_{где  , тогда} 

Полная механическая энергия р авна сумме кинетической и потенциальной энергий,

и в случае свободных колебаний без трения сохраняется (рис.1.1.15).

Когда материальная точка совершает колебания, кинетическая энергия переходит в потенциальную, и наоборот.

В крайних точках (х = ±А) скорость  , кинетическая энергия равна нулю, и полная энергия равна потенциальной:

Таким образом, полная механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия (х=0) потенциальная энергия переходит в кинетическую:

В промежуточных точках полная энергия равна

_{аскорость} 

На рисунке 1.1.16 приведена кривая потенциальной энергии  :

- горизонтальная линия соответствует полной энергии.

- расстояние от этой линии до кривой  равно кинетической энергии.

-движение ограничено значениями х,заключёнными в пределах от–Адо +А.

Средние за период значения кинетической и потенциальной энергии одинаковы и равны

,

так что средняя полная энергия системы равна полной энергии системы

( средние значения  ).