21. Момент импульса частицы и момент силы относительно некоторой точки. Уравнение моментов.

22. Момент импульса системы. Законы изменения и сохранения момента импульса системы.

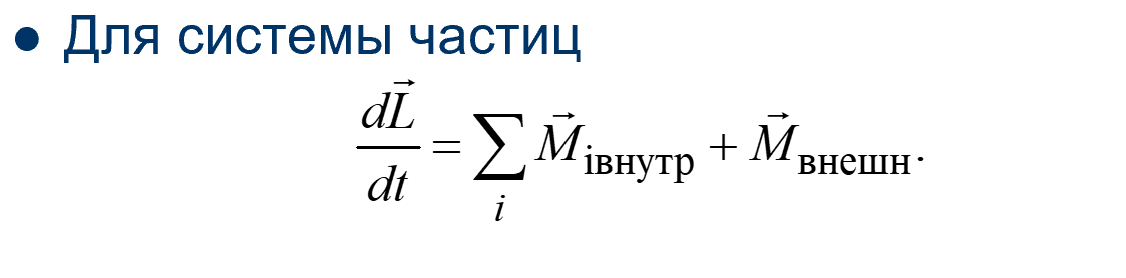
23. Число степеней свободы твердого тела. Уравнения движения твердого тела.

Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета. Движение твердого тела во многом зависит от числа его степеней свободы.

Число степеней свободы твердого тела

Абсолютно твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени.

Чтобы однозначно определить положение твердого тела достаточно задать положение каких-либо трех точек А, В, С, не лежащих на одной прямой. Положение точек можно задать их прямоугольными координатами 

Эти девять координат, однако, не независимы, а связаны тремя соотношениями:

поскольку длины АВ, АС, ВС не изменяются при движении твердого тела. Независимых координат остается только шесть – твердое тело имеет шесть степеней свободы. Отметим, что твердое тело, одна из точек которого неподвижно закреплена, может только вращаться вокруг этой неподвижной точки, имеет три степени свободы. Твердое тело, которое может только вращаться вокруг закрепленной оси, имеет одну степень свободы.

Если же твердое тело может скользить вдоль закрепленной оси и одновременно вращаться вокруг нее, то число степеней свободы равно двум.

Уравнение движения и равновесия твердого тела

Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.

Одно из них – это уравнение движения центра масс С

, где  . (1)

Второе – уравнение моментов

. (2)

Если твердое тело покоится, то уравнения (1) и (2) переходят в

. (3)

+Это необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением момента импульса. Такое движение твердого тела называют свободным. Следует отметить, что даже свободное движение твердого тела может быть очень сложным. Поэтому сначала рассмотрим простейший случай движения твердого тела.

24. Момент импульса тела относительно точки. Момент инерции тела относительно оси. Теорема Штейнера.

Моментом импульса материальной точки а относительно неподвижной точки 0 называется физическая величина, равная векторному произведению

, (20)

где  - радиус-вектор проведенный из точки 0 в точку а, - импульс материальной точки.

+Рис.9.

Направление вектора  совпадает с направлением поступательного движения правого винта при его вращении от к . Модуль вектора момента импульса

(21)

где  - угол между векторами и , - минимальное расстояние от точки к точке 0. Моментом импульса системы материальных точек относительно неподвижной точки 0 называется векторная сумма моментов импульсов всех материальных точек системы относительно той же точки 0

(22)

Момент инерции I твердого тела относительно некоторой неподвижной оси (осевой момент инерции) – скалярная физическая величина, являющаяся наряду с массой количественной мерой инертности этого тела при его вращательном движении вокруг данной оси, и равная:

a – расстояние между осями.