67. Вектор магнитной индукции. Магнитное поле равномерно движущегося заряда

Магнитная индукция – вектор, направление которого определяется равновесным направлением положительной нормаль к пробному контуру. Магнитная индукция характеризует силовое действие магнитного поля на ток. течет ток

Как известно, электрический ток – упорядоченное движение зарядов, а, как мы доказали только, что, магнитное поле порождается движущимися зарядами. Найдем магнитное поле, создаваемое одним движущимся зарядом. В уравнении (1.2.2) заменим ток I на jS, где j – плотность тока. Векторы имеют одинаковое направление, значит Если все заряды одинаковы и имеют заряд q, то , где n – число носителей заряда в единице объема; – дрейфовая скорость зарядов. Если заряды положительные, то  и  имеют одно направление (рис. 1.4). Подставив (1.3.1) в (1.2.2), получим:  Обозначим – число носителей заряда в отрезке  Разделив (1.3.2) на это число, получим выражение для индукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью  : В скалярной форме индукция магнитного поля одного заряда в вакууме определяется по формуле: Эта формула справедлива при скоростях заряженных частиц

68.Стационарное магнитное поле. Закон Био-Савара-Лапласа

Стационарным магнитным полем называется магнитное поле постоянного тока. Это поле соответствует режиму установившегося движения зарядов.

Закон Био-Савара-Лапласа

Этот закон определяет модуль и направление вектора магнитной индукции поля, создаваемого проводником с током произвольной формы. Согласно принципу суперпозиции, магнитное поле проводника с током в определенной точке пространства можно найти как суперпозицию полей, создаваемых отдельными элементами этого проводника: .(8.1)

Здесь – магнитная постоянная, в системе СИ равная Гн/м, – сила тока в проводнике, – вектор элемента проводника, направленный вдоль тока, – радиус-вектор, проведенный от элемента в рассматриваемую точку поля (точку наблюдения).

В качестве примера найдем индукцию магнитного поля, создаваемого длинным прямолинейным проводником с током в точке, удаленной от него на расстояние 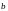. Согласно равенству (8.1), , где вектор в точке наблюдения направлен в плоскость рис. 8.1. На этом же рисунке видно, что

.

Рис. 8.1

Поскольку для всех элементов проводника бесконечной длины угол изменяется от нуля до , имеем: .

По аналогии с линиями напряженности электрического поля, для графического изображения стационарных магнитных полей используются линии индукции. Они проводятся так, что касательная к линии в определенной точке указывает направление вектора магнитной индукции, а густота линий пропорционально его модулю. Поскольку источником магнитного поля являются токи, линии индукции всегда замкнуты; именно поэтому магнитное поле относится к вихревым (соленоидальным) полям.

Магнитное поле называется однородным, если в каждой его точке вектор магнитной индукции имеет одинаковый модуль и направление. Как и в случае однородного электростатического поля, линии индукции однородного магнитного поля представляют собой параллельные равноотстоящие линии. Согласно закону Био-Савара-Лапласа линии индукции магнитного поля прямолинейного проводника с током представляют собой концентрические окружности, центры которых расположены на проводнике.