№63 Электрическое поле диполя в дальней зоне

Диполь – это совокупность двух равных по величине разноименных точечных зарядов, расположенных на расстоянии друг от друга.

Потенциал - это скалярная энергетическая характеристика электростатического поля. Численно равная потенциальной энергии, которой обладал бы заряд помещенный в ту же точку.

Напряженность - векторная силовая характеристика электростатического поля. Численно равная силе, действующей на положительный заряд, помещённый в туже точку.

эквипотенциальные поверхности –это поверхность в каждой точке которого потенциал равен const или он постоянный.

№64 Момент сил, действующих на диполь в электрическом поле.

Потенциальная энергия диполя в электрическом поле.

Плечо диполя  — вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними.

Электрический момент диполя р — вектор, совпадающий по направлению с плечом диполя, направленный от отрицательного заряда к положительному и равный произведению модуля заряда q на плечо

Момент сил, действующий на диполь. Во внешнем электрическом поле на заряды диполя действует пара сил, которая стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля Ё.

Энергия диполя в поле. По формуле (12.17) энергия точечного заряда во внешнем поле W — qq>, где φ — потенциал поля в точке нахождения заряда q. Поэтому энергия диполя во внешнем поле

№65 Плотность и сила тока. Основные теории Друде для классической электропроводности металлов.

Электрический током называется всякое упорядоченное движение электрических зарядов (заряженных частиц).

Плотностью тока называется физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока: Направление вектора j совпадает с направлением упорядоченного движения положительных зарядов.

Сила тока – это скалярная физическая величина, численно равная заряду, переносимому через произвольную поверхность в единицу времени.

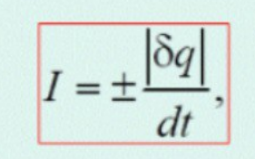
Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют "электронный газ". №66 Уравнение непрерывности. Закон Ома в локальной (дифференциальной) форме.

Уравнение непрерывности гласит, что если заряд уходит из дифференциального объёма (то есть дивергенция плотности тока положительна), тогда количество заряда внутри объёма уменьшается. В этом случае приращение плотности заряда отрицательно. Если сила тока не меняется во времени, то ток, протекающий в проводнике, называют постоянным. В силу закона сохранения заряда эта величина должна быть равна скорости убывания заряда, содержащегося в данном объеме Это соотношение называют уравнением непрерывности.

Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС): 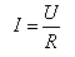Для однородного линейного проводника выразим R через ρ(удельное сопротивление): Найдем связь между и в бесконечно малом объеме проводника – закон Ома в дифференциальной форме. В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока и вектор напряженности поля коллинеарны.

 Исходя из закона Ома:

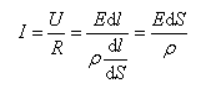.   А мы знаем, что   или  . Отсюда можно записать 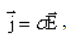это запись закона Ома в дифференциальной форме. Здесь   – удельная электропроводность.