52. Распределение молекул идеального газа по координатам во внешнем поле (распределение Больцмана).

Распределением Больцмана называют распределение вида

Где Ер- потенциальная энергия молекулы mgh, n0- число молекул в единице объема в том месте, где потенциальная энергия молекулы равна нулю, n- число молекул в единице объема в точке пространства, где потенциальная энергия равна Ер.

Данное распределение справедливо в любом потенциальном поле сил для совокупности одинаковых частиц, находящихся в состоянии хаотического теплового движения.

Распределение Больцмана выводится из барометрической формулы

Заменой р на n (через формулу nkT) и заменой отношения µ/R на равное ему отношение m/k. Получаем:

!Поведение газа не изменится, если вместо силы тяжести на него будет действовать другая сила!

Данная формула описывает изменение концентрации молекул от высоты h в потенциальном поле земного тяготения и от температуры Т.

Из нее следует, что с понижением температуры число частиц убывает, обращаясь в нуль при Т=0. При абсолютном нуле все молекулы расположились бы на поверхности земли, при пошенных температурах наоборот, все молекулы окажутся распределны по высоте почти равномерно.

Можно отметить две тенденции, определяющих распределение молекул по высоте:

1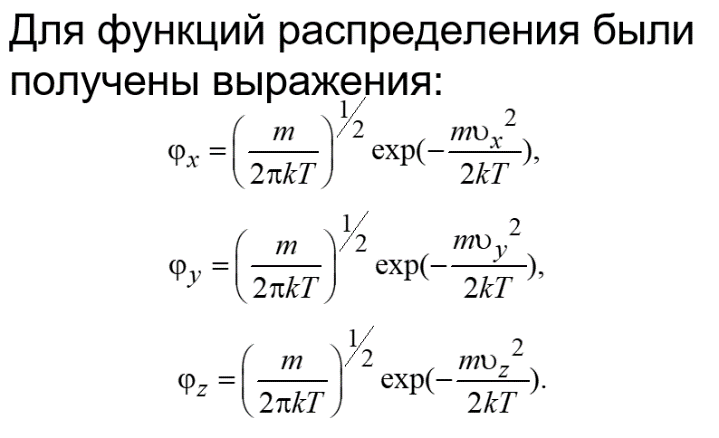 . Притяжение молекул к Земле (mg) стремится расположить их на поверхности Земли.

2. Тепловое движение (kT) стремится разбросать молекулы равномерно по всем высотам от 0 до 

53. Распределение Максвелла-Больцмана

Распределения Максвелла и Больцмана можно объединить в один закон Максвелла-Больцмана, который описывает распределение молекул газа по координатам и скоростям при системном воздействии внешнего потенциального поля.

По распределению Максвелла-Больцмана число молекул, содержащихся в единице объема, и скорость которых лежит между v и v+dv равно:

Е- полная механическая энергия молекулы, n0- число молекул в единице объема в точке, где потенциальная энергия молекулы равна нулю.

Результат интегрирования по v: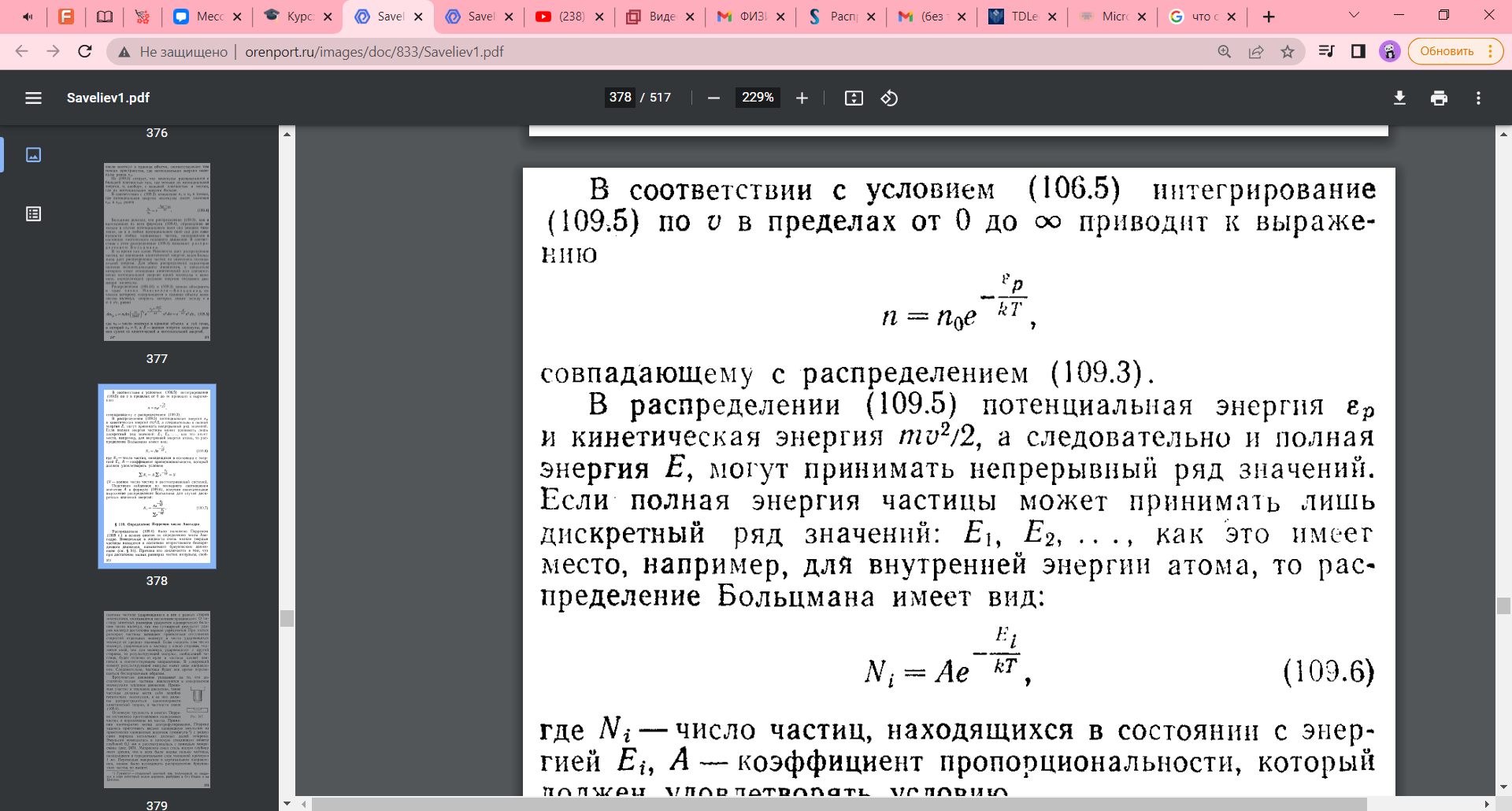

В данной формуле потенциальная и кинетическая энергии, следовательно, и полная энергия, могут принимать непрерывный ряд значений. Если полная энергия может принимать лишь дискретные значения, то распределение Больцмана принимает вид:

Где N- число частиц, находящихся в состоянии с энергией E, A - коэффициент пропорциональности, который должен удовлетворять условию: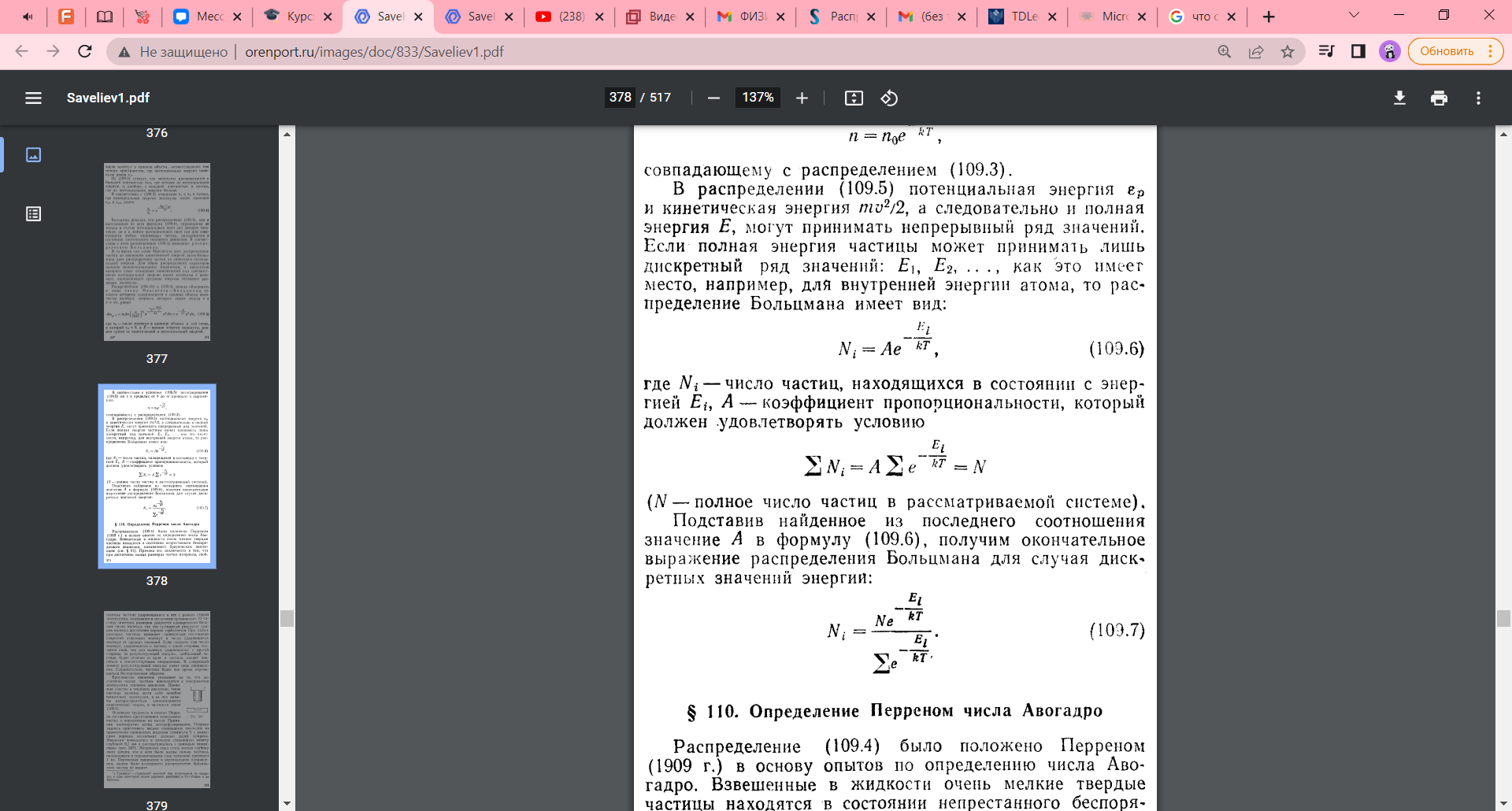

Подставим отсюда значение А в формулу и получим окончательную формулу распределения Больцмана для дискретных энергий:

54. Закон равнораспределения энергии по степеням свободы. Статистический смысл температуры.

Закон о равнораспределении энергии по степеням свободы:

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы.

Средняя энергия молекулы должна равняться

Где i - число степеней свободы молекулы. У одноатомной молекулы 3 степени свободы, у двухатомной – 5 степеней свободы, у трёхатомной – 6 степеней свободы.

Статистический смысл температуры:

Абсолютная температура есть величина, пропорциональная средней энергии движения одной молекулы.