44. Внутренняя энергия идеального газа. Теплообмен и количество теплоты. Работа сил давления газа. Первое начало термодинамики.

Внутренняя энергия идеального газа – это сумма кинетических энергий движения молекул. Потенциальные энергии не учитываются, потому что газ является идеальным (не учитывается взаимодействие молекул).

Внутренняя энергия U одного моля идеального одноатомного газа равна:

Теплопередача (теплообмен) - процесс изменения внутренней энергии без совершения работы. Количественная характеристика - количество теплоты - часть изменения внутренней энергии, происходящего в процессе теплопередачи. Обозначается Q. Единицы измерения: Дж

Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную.

А=p (V2-V1)

45. Теплоемкость как функция термодинамического процесса. Уравнение Майера

Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус

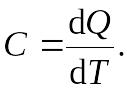
Удельная теплоёмкость (Суд) – есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С_V.

Уравнение Майера:

Это уравнение Майера для одного моля газа. Из него следует физический смысл универсальной газовой постоянной R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе.

46. Адиабатический процесс. Уравнение Пуассона

Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.

Уравнение Пуассона описывает адиабатный процесс, протекающий в идеальном газе. Адиабатным называют такой процесс, при котором отсутствует теплообмен между рассматриваемой системой и окружающей средой: 

Уравнение Пуассона имеет вид:

Здесь V – объем, занимаемый газом, P – его давление, а величина k называется показателем адиабаты.

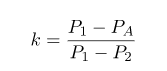
47. Термодинамический цикл. Кпд цикла

Тепловые двигатели работают таким образом, что газ (рабочее тело) расширяется в результате получения теплоты 1 Q от источника, имеющего высокую температуру. Для того чтобы вернуться в первоначальное состояние, можно снова сжать рабочее тело, но при этом полезная работа получена не будет. Для получения полезной работы необходимо в процессе расширения понизить давление газа путем отвода от него части теплоты Q к 2 источнику с более низкой температурой.

Прямой цикл реализуется в тепловом двигателе − периодически действующем устройстве, которое совершает работу за счет полученной от нагревателя теплоты Q. Обратный цикл используется в холодильных установках − периодически действующих устройствах, в которых за счет работы А внешних сил теплота переносится от более холодного тела к телу с более высокой температурой.

Рассмотрим принцип действия теплового двигателя (рис. 12.8.1). В тепловом двигателе от нагревателя с температурой Т1 за цикл отнимается количество теплоты Q1 , а холодильнику с более низкой температурой (T2 < T1) за цикл передается количество теплоты Q2 . При этом совершается работа. Поскольку термодинамическая система (тепловая машина) за цикл возвращается в исходное состояние (внутренняя энергия оказывается прежней), то на основании первого начала термодинамики получим значение работы теплового двигателя за цикл:

Термический коэффициент полезного действия (КПД) определяется отношением: Рассмотрим принцип действия холодильной установки (рис. 12.8.1). В холодильной установке за счет совершения внешними силами работы А от более холодного тела с температурой T2 за цикл отнимается количество теплоты Q2 и отдается во внешнюю среду с температурой (Т1 > Т2) количество теплоты, равное Q1 . Для оценки эффективности работы холодильной установки используют отношение количества теплоты, отнятого за цикл от холодильной камеры, к работе А внешних сил. Эта величина называется показателем цикла k, или холодильным коэффициентом:

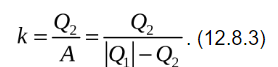
48. Цикл Карно. КПД цикла Карно

Цикл Карно – идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов.

КПД машины Карно равен отношению разности абсолютных температур нагревателя и холодильника к абсолютной температуре нагревателя. Площадь, ограниченная изотермами и адиабатами, численно равна работе цикла Карно.

49. Понятие функции распределения плотности вероятности случайной величины.

Это функция характеризующая распределение случайной величины или случайного вектора. ( она же интегральная функция распределения вероятностей) – это вероятность того, что случайная величина (назовем ее ξ) примет значение меньшее, чем конкретное числовое значение X:

5 0. Распределение Максвелла

51. Средняя, среднеквадратичная и наиболее вероятная скорости молекул

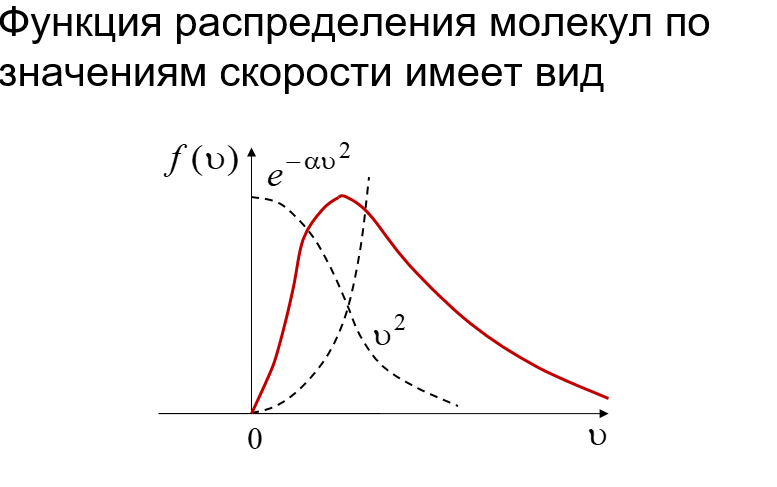
Функция распределения молекул по скоростям (функция распределения Максвелла) имеет вид:

Где это величина А, называющаяся нормированным множителем. Тогда формула распределения Максвелла принимает вид:

При ее помощи получим значения средней, среднеквадратичной и наиболее вероятной скоростей молекул.

Наиболее вероятная скорость

Наиболее вероятной в данном случае будет максимальная скорость. Следовательно, найдя максимум функции f(v) найдем наиболее вероятную скорость.

Продифференцируем выражение по скорости и приравняем к нулю:

Значение v, обращающее в нуль выражение в скобках и будет искомой скоростью.

Средняя скорость молекул

Разобьем ось скоростей на малые интервалы. Каждому интервалу соответствует количество молекул:

Скорость каждой из Ni молекул будем считать приближенно равной v, так как интервал vi бесконечно мал. Тогда сумму всех скоростей можно представить в виде интеграла суммы

Ч тобы получить среднюю скорость, разделим сумму скоростей на число молекул N. Тогда

Перейдем к интегралу:

Подставим нашу функцию f(v) в полученный интеграл. Получим формулу вычисления средней скорости:

Средняя квадратичная скорость молекул

Аналогичным образом получаем значения для среднего значения квадрата скорости. Получаем: