1 Вопрос:

Материальная точка – это тело, размерами которого в условиях данной задачи можно пренебречь. Это бывает в тех случаях, когда размеры тела во много раз меньше прочих размеров, с которыми приходится иметь дело в условиях данной задачи. Например, при определении пути, проходимого автомобилем при переезде из Ленинграда в Москву, размерами автомобиля вполне можно пренебречь; при вычислении траектории, по которой Земля движется вокруг Солнца, Землю можно рассматривать как материальную точку. Но при рассмотрении движения тел по поверхности Земли она должна рассматриваться как протяженное тело.

Твёрдое тело – это тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь. Движение тел обычно происходит в условиях, когда на них действуют силы. Действие этих сил наряду с тем, что определяет характер движения, вызывает также деформацию. Очень часто деформации настолько незначительны, что ими можно пренебречь при описании движения тела. Следует иметь в виду, что абсолютно твёрдых тел в природе не существует. Только пренебрежимо малая роль деформаций при движении тел в определённых условиях даёт возможность рассматривать их как абсолютно твёрдые.

Движение одного и того же тела относительно различных тел может иметь разный характер. Если тело 1 относительно нас покоится, а тела 2 и 3 движутся в одну и ту же сторону с одинаковой скоростью, то тело 3 перемещается относительно тела 1, однако покоится относительно тела 2. Поэтому для описания движения необходимо условиться, относительно какого другого тела (или группы неподвижных друг относительно друга тел) будет отсчитываться перемещение данного тела. Выбранное для этой цели тело (или группа тел) образует систему отсчёта.

Число степеней свободы системы — это число независимых координат, которые необходимо задать для однозначного определения положения системы в пространстве. Координаты не обязательно декартовы. Независимость координат означает, что система допускает изменение каждой из них при неизменности остальных. Частица в пространстве имеет 3 степени свободы (x, y, z), на поверхности – 2 (x, y), на заданной кривой – 1 (только х).

2 Вопрос:

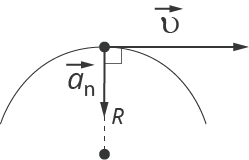Кинематика изучает движение тел вне зависимости от тех причин, которые обусловливают это движение. Материальная точка при своём движении описывает некоторую линию. Эта линия называется траекторией. Пусть материальная точка переместилась вдоль некоторой траектории из точки 1 в точку 2. Расстояние от точки 1 до точки 2, отсчитанное вдоль траектории, представляет собой пройденный путь. Вектор, проведённый из точки 1 в точку 2, называется перемещением.

3 Вопрос:

Кинематика изучает движение тел вне зависимости от тех причин, которые обусловливают это движение. Радиусом-вектором точки называется вектор, проведённый из начала координат в данную точку. Скоростью называется предел, к которому стремится отношение r к t при неограниченном убывании t. Следовательно, скорость можно определить как производную радиус-вектора движущейся точки по времени. Док-во: при движении точки вектор r изменяется и по величине, и по направлению. Зафиксируем некоторый момент t. Ему соответствует значение r радиуса-вектора. В течение следующего за моментом t небольшого промежутка времени дельта t точка проходит элементарный путь s и получает элементарное перемещение дельта r, которое совпадает с приращением радиуса-вектора за время дельта t^2. Образуем отношение При данном t модуль и направление вектора зависят от величины промежутка дельта t. При достижении достаточно малых значений времени вектор практически перестаёт изменяться как по величине, так и по направлению. Это означает, что при стремлении изменения времени к 0 отношение стремиться к определённому пределу

Быстрота изменения скорости материальной точки со временем характеризуется величиной Эта величина называется ускорением точки.

При малых изменениях времени Если известна величина скорости как функция времени, можно вычислить путь, пройденный точкой с момента до момента . Для этого разобьём промежуток времени промежутков, которые могут быть различными по величине. Весь путь можно представить как сумму путей, пройденных за соответствующие промежутки времени . Отсюда следует, что , т.к. . Написанное равенство выполняется тем точнее, чем меньше промежутки времени В пределе при стремлении всех к 0 сумма, стоящая справа, станет точно равна пути . Скорость есть функция времени . 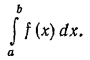В математике выражение вида , составленное для значений х, заключенных в пределах от а до б, называют определённым интегралом и записывают символически следующим образом: Следовательно, путь, пройденный точкой за промежуток времени равен определённому интегралу .