Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра физики

Лабораторная работа № 3э.3

«Изучение магнитных полей»

Проверил:	Доцент кафедры физики
	Смирнова Г.Ф.

Минск 2022

Цель работы:

1. Ознакомиться с одним из методов измерения индукции магнитного поля.

2. Изучить магнитное поле тока катушки.

3. Проверить справедливость принципа суперпозиции магнитных полей.

Схема установки:

Основные формулы:

Таблица измерений:

х,10-2,м	L1		L2		B1x + В2х, Тл	L1 и L2
	U1, 10-3, B	B1x, Тл	U2, 10-3, B	B2x, Тл		U, 10-3, B	Bpx, Тл
-4	72	0,101535211	-744	-1,0492	-0,947661972	-776	-1,09432
-3	102	0,143841549	-616	-0,86869	-0,724848592	-664	-0,93638
-2	136	0,191788732	-464	-0,65434	-0,462549296	-488	-0,68818
-1	196	0,276401408	-336	-0,47383	-0,197429577	-288	-0,40614
0	240	0,338450704	-252	-0,35537	-0,016922535	-104	-0,14666
1	328	0,462549296	-188	-0,26512	0,197429577	88	0,124099
2	456	0,643056338	-128	-0,18051	0,462549296	280	0,394859
3	600	0,846126761	-94	-0,13256	0,713566901	472	0,66562
4	752	1,060478873	-80	-0,11282	0,947661972	664	0,93638

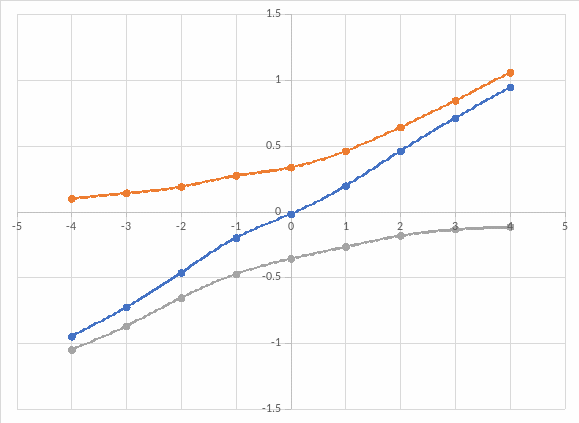
Вывод:

В ходе выполнения работы мы изучили динамику вращательного движения твердого тела вокруг неподвижной оси, изучили деформацию сдвига и кручения, изучили динамику и кинематику свободных незатухающих гармонических крутильных колебаний. Определили моменты инерции тела относительно различных осей и модуль сдвига материала проволоки методом крутильных колебаний.

Контрольные вопросы

1. Заряды, проводники с током и тела с магнитным моментом являются источниками магнитных полей, которые в свою очередь воздействуют на движущиеся электрические заряды и тела с магнитным моментом. Магнитное поле возникает из-за движения заряженных микрочастиц и их собственного магнитного момента. Метод расчета магнитных полей основан на принципе суперпозиции, то есть векторная сумма магнитных полей, порождаемых каждым зарядом или током в данной точке, равна магнитному полю, порождаемому несколькими зарядами или токами.

2. Закон Био-Савара-Лапласа — магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

Направление вектора определяется правилом буравчика (правой руки): оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока.

3. Явление электромагнитной индукции заключается в том, что изменение магнитного поля в проводящей петле вызывает появление электрического тока. Майкл Фарадей открыл это явление в 1831 году. Например, перемещение магнита относительно проводящей петли вызывает электрический ток в петле. При включении тока в катушке, создающей магнитное поле, в измерительной катушке возникает индуктивный ток, направленный противоположно направлению тока в катушке. При выключении тока в катушке, создающей магнитное поле, в измерительной катушке возникает индуктивный ток, направленный в том же направлении, что и ток в катушке.

4. В методе исследования магнитного поля катушек используются следующие физические явления:

Явление электромагнитной индукции, описанное выше.

Закон Ома, согласно которому сила тока пропорциональна напряжению и обратно пропорциональна сопротивлению проводника.

Закон сохранения энергии, согласно которому энергия не может быть создана или уничтожена, а может только преобразовываться из одной формы в другую.

Закон Био-Савара-Лапласа, описывающий взаимодействие магнитных полей и токов.

Закон Фарадея, описывающий явление электромагнитной индукции и связь между магнитным полем и электрическим током.

5. Измерительная катушка (зонд) жестко закреплена на стержне и может перемещаться вдоль осей катушек L1 и L2. К измерительной катушке подключена емкость C. В переходном процессе полное сопротивление измерительной цепи R равно сумме сопротивлений зонда, соединенных проводов и осциллографа. С помощью потенциометра изменяется сила тока в катушках L1 и L2. На конденсаторе C отображается числовое значение амплитуды напряжения U, которое указывается как Vamp в меню, расположенном в правой части экрана осциллографа.

6. Закон Био-Савара-Лапласа гласит, что магнитное поле dH, создаваемое элементом тока Idl, расположенным на расстоянии r от точки наблюдения, определяется следующей формулой:

dH = (μ₀/4π) * (Idl x r) / r³,

где μ₀ - магнитная постоянная, Idl - элемент тока, r - расстояние от элемента тока до точки наблюдения.

Для вычисления магнитного поля в центре круговой петли радиусом R, по которой течет ток I, можно использовать принцип суперпозиции магнитных полей. Мы можем разбить круговую петлю на маленькие элементы длиной dl и найти магнитное поле dH, создаваемое каждым элементом тока. Затем мы можем проинтегрировать все элементы тока по всей длине петли, чтобы получить общее магнитное поле в центре петли.

Используя геометрические соображения, мы можем выразить расстояние r от элемента тока до точки наблюдения в центре петли как:

r = sqrt(R² + x²),

где x - расстояние от центра петли до точки наблюдения.

Заменим в формуле для dH значение r:

dH = (μ₀/4π) * (Idl x r) / r³ = (μ₀/4π) * (Idl x r) / (R² + x²)^(3/2) = (μ₀/4π) * (Idl x R) / (R² + x²)^(3/2),

так как элемент тока Idl и вектор r перпендикулярны, то их векторное произведение Idl x r можно заменить на Idl x R, где R - радиус вектор центра петли.

Используя принцип суперпозиции, мы можем проинтегрировать dH по всей длине петли:

B = ∫dH = (μ₀/4π) * I ∫(dl x R) / (R² + x²)^(3/2),

где интеграл берется по всей длине петли.

Обратим внимание, что dl x R является векторным произведением длины элемента тока и радиуса вектора центра петли. Так как длина элемента тока находится на расстоянии R от центра петли, то можно записать dl = R*dφ, где dφ - малый угол, на который повернулся элемент тока относительно центра петли.

Тогда интеграл примет вид:

B = (μ₀/4π) * I ∫(R*dφ x R) / (R² + x²)^(3/2) = (μ₀/4π) * I ∫R² * dφ / (R² + x²)^(3/2).

Интегрируя по всей длине петли от 0 до 2π, получим:

B = (μ₀/4π) * I * 2π * R² / (R² + x²)^(3/2) = (μ₀/2) * (I * R²) / (R² + x²)^(3/2)