Алгоритмы Конечные автоматы
Конечный автомат называется детерминированным (ДКА) если Pj содержит не более одного состояния
Конечный автомат называется недетерминированным (НДКА) если Pj содержит более одного состояния
НДКА
НДКА
Рассмотрим НДКА. |
|
||
Начальное состояние автомата q0 |
|
||
Пусть на вход автомата поступает последовательность |
|
||
100 100 |
|
|
|
до |
вход |
Переход |
После |
q0 |
1 |
из q0 по символу 1 только |
q0 |
|
|
в одно состояние q0 (cм. |
|
|
|
схему) |
|
q0 |
0 |
из q0 по символу 0 автомат может |
q0 ,q1 |
|
|
перейти в два состояния q0 и q1 |
|
НДКА
до |
вход |
Переход |
После |
q0, |
0 |
из q0 по символу 0 автомат может |
q0 ,q1, q2 |
|
|
q1 |
|
перейти в два состояния q0 и q1; |
|
|
из состояния q1 сущетвует только |
|
|
один переход в q2. Поскольку автомат |
находиться в двух состояниях , то множества объединяются
Тогда на выходе (после, см. правую колонку) получим q0,q1,q2
НДКА
до |
вход |
Переход |
После |
q0, |
1 |
автомат находиться в трех состояниях, |
|
|
|
но из q1 и из q2 не существует переходов |
q0 |
q1, |
|
по символу 1 (т.е. значение функции пере |
|
q2 |
|
ходов по входному символу 1 - пустое |
|
|
|
множество). В итоге остается только q0 |
|
q0 |
0 |
анлогично получаем |
q0,q1 |
q0, 1 q0,q1,q2
q1
НДКА
Рассмотренные исследования поведения автомата можно проследить на ветвящейся схеме:
напр. видно , что при приходе символа 0 автомат переходит сразу в два состояния q0 и q1.
(т.е. добавляется новая ветка вычислений) Когда переходов нет ветка обрывается.
Вывод : необходимо преобразовать НДКА в ДКА
Алгоритмы Конечные автоматы
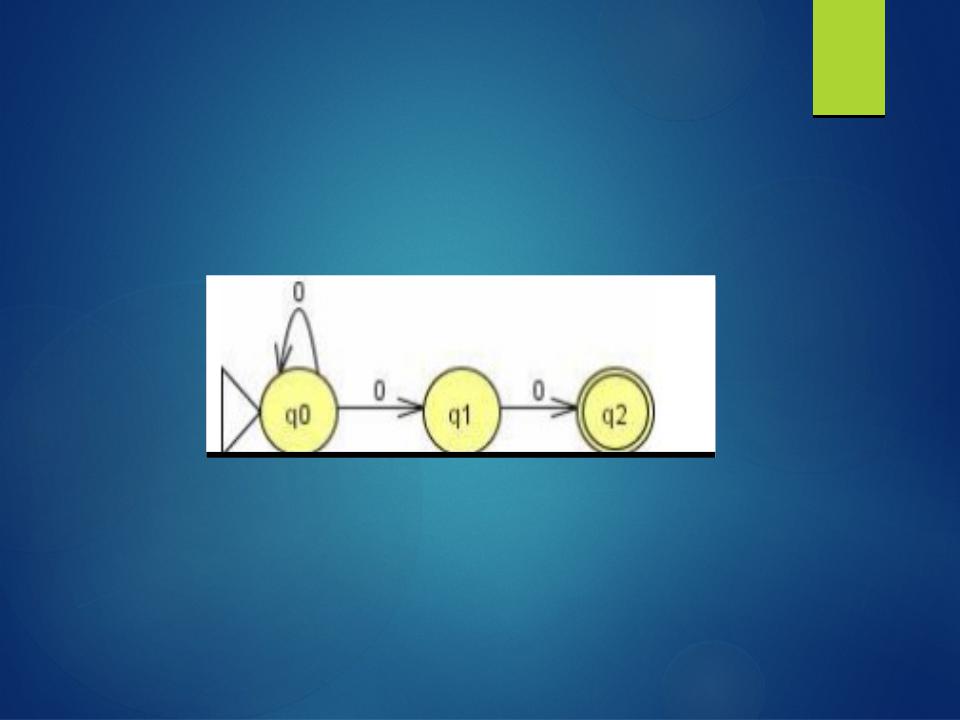
ДКА
Как видно из рис. автомат может переходить только в одно состояние.
Переход от НДКА к ДКА
