1. Строка – это конечная последовательность символов а₁, а₂,…,а_n, каж-й из кот-х принадлежит некоторому конечному алф-ту Σ, при этом символы в строке могут повторяться.

Если некоторая срока z м.б.представлена как объединение строк х и у: z=ху, то строку х наз-т префиксом строки z, а строку у-суффиксом. Если строку z т.ч.ее м/о представить как объединение 3х строк z=xwy, то строка w н-ся подстрокой строки z.

префиксы: ε,a,ac,aca,acab

суффиксы: ε,b,ab,cab,acab

подстроки: ε,a,b,c,ac,ca,ab,aca,cab,acab

Язык – всякое средство общения, которое состоит из 3 вещей:

1. Допустимые последовательности знаков

2. Множества смыслов системы

3. Соответствие между этими знаками и смыслами

[В общем понимании формальный язык – язык программирования высокого уровня, используемый при создании алгоритмов человеком.]

Формальным языком L над алф-ом Σ н-ся произвольное подмн-во мн-ва Σ^*, которое является множеством всех возможных строк, то есть формальный язык – подмножество, состоящее из возможных для составления с данным алфавитом строк.

Если L₁ и L₂ это 2а формальных языка, то их объединение есть нов.форм.язык, т.ч.L= L₁L₂{xy| хL₁,уL₂ }

// L₁={0,01} и L₂={ε,0,10}значит L= L₁L₂={0,01,00,010,010,0110}

L⁰= ε, L¹=L, L²=L*L -объединение форм.языка L с самим собой:

Терминальный символ – символ, который имеет конкретное значение.

Нетерминальный символ – символ, который не имеет конкретное символьное значение.

2. [Дерево вывода – разбиение выходной информации на выходные части графически*]

Дерево вывода - способ представления множества выводов одной и той же цепочки в грамматике.

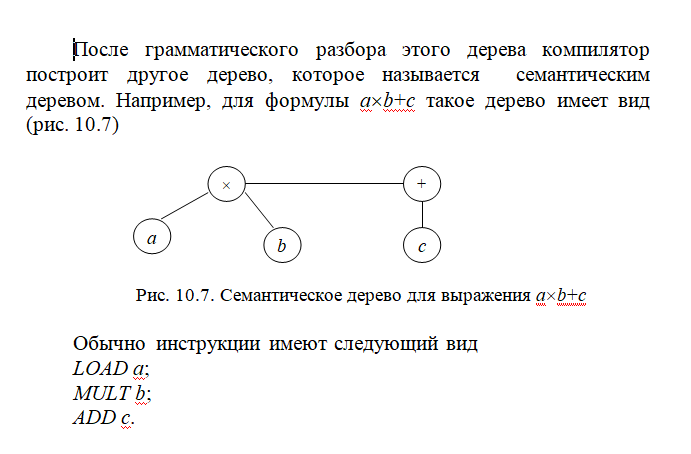
Семантическое дерево — способ представления множества выводов, который отражает семантику (интерпретацию/последовательность действий) выходных конструкций явно содержит в себе полную взаимосвязь операций.

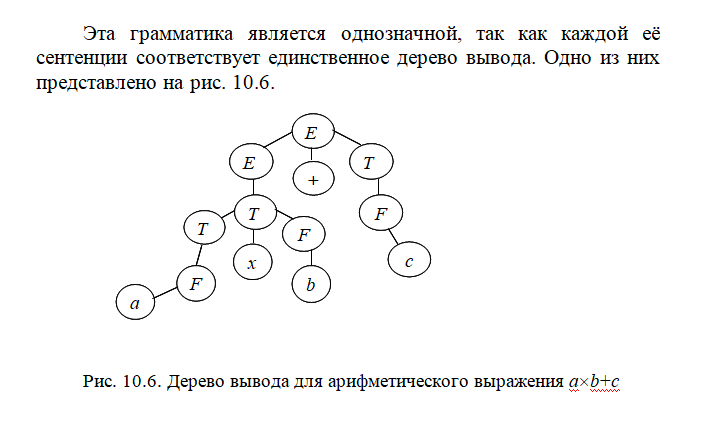
Синтаксическое дерево  — способ представления множества выводов, который отражает синтаксис выходных конструкций и явно отражает взаимосвязь продукций языка.

3. Контексная гр-ка(К/Г) –

–

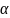– строка нетерминальных или терминальных символов, длиной >0, а 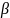– та же строка, но любой длины.

4. 

Пусть дана К/гр-ка G=(N,T,P,S), и есть строка γ₁α γ₂ (NUT)⁺, кот.содержит не менее одного термин-го или нетерм-го сим-ла. Если сущ-ет вывод α →β, то в дан.строке α м/о заменить на β – получится новая строка γ₁βγ₂. След-но, 2-ая строка выводится из 1-ой или 1-ая строка пораждает 2-ю.

Если строка α(NUT)^* за 1н или неск-ко шагов выводится из начального сим-ла S, то такую строку наз-т сентенциальной формой К/Г-ки G.

+Сентенцией гр-ки G наз-т произ-ю сентенциальную форму, составл-ю из симв-в мн-ва Т^*, т.е.произ.строку терм.сим-в, кот-я м.б.получена из нач-го сим-ла S. Тогда мн-во всех сентенций гр-ки G наз-т языком, пораждаемым гр-кой G и обоз-т L(G). Концепция пораждения им.вид

L(G)={x Т^* |S _G^*х}. Символ  _G^*означает, что строка х выводится из нач-го символа S за 1н или неск-ко шагов по правилам гр-ки G.

//G₁=({S,A,B},{a,b},P,S); P: S→A|B, A→aA|a, B→bB|b.

G₂=({S,B,C},{a,b,c},P,S); P: S→aSBC|aBC, CB→BC, aB→ab, bB→bb, bC→bc, cC→cc.

м/о показать, что гр-ки G₁ и G₂ пораждают следующие языки:

L(G₁)={aⁿ|n1}U{ bⁿ|n1} и L(G₂)={aⁿbⁿcⁿ|n1}

+Иногда 2е различные гр-ки GиG’пораждают один и тот же язык, т.е. L(G)=L(G’). След-но гр-ки GиG’эквивалентны.

// гр-ка G₃= ({S,A,B},{a,b},P,S); P: S→aA|bB|a|b, A→aA|a, B→bB|b.эквивалентна гр-ке G₁.

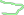
Для рассм-ия св-в всего мн-ва гр-к их н/о классиф-вать по опред.признакам. Наиболее эффективной оказалась класс-ия предлож-ая Хомским. Согластно этой классиф-ии все гр-ки делятся на 4 типа: 0,1,2,3.

1. гр-ка произвольного типа, без ограничений на правила вывода.

2. если правило вывода прод-ии предст-ет собой α→β, где α=γ₁ х γ₂, β = γ₁ δ γ₂ – строки, где γ₁и γ₂ (NUT)^*, хΝ, δ (NUT)⁺, то такая гр-ка наз.контекстно-зависимой или 1-го типа.

3. КС/Г-ка, для кот-й все правила вывода им.вид: α→β, где αN, β(NUT)^*.

4. Регулярная(автоматная гр-ка), правила вывода кот-й: А→а, А→аВ, где АN, ВN, аТ.

6. Регулярная грамматика – нотации БНФ, в которых правая часть представляет собой либо один терминальный символ, либо последовательность терминальных и нетерминального символов.

К/Г-ка G=(N,T,P,S) наз.регул-ой, если:

1.ее продук-ии им.вид А→а или А→аВ, где АN, ВN, аТ.

2.она м/т им.ε-продукцию вида: S→ε и ни одна из др-х продук-й гр-ки G не содержит в своей правой части символа S.

S→аS|aB;

B→bB|b.

S→ε|аS₁|aB;

S₁→аS₁|aB;

B→bB|b.

Люб.регулярная гр-ка м.б.представлена направленным графом. Каж.узел помечается симв-м из мн-ва N. Нач.сим-л S помечают стрелкой, конеч-й обозн-т #.

S→аА|bB;

A→aA|a;

B→ bB|b.

+Направленный граф, который имеет 1 начальный узел и 1 или несколькоко конечных узлов наз-ся конечным авт-м.

Также: Конечный автомат – матем. модель реального дискретного устройства, которая под воздействием конечного множества входных сигналов переходит из одного состояния в другое (из конечного множества состояний), с выработкой сигнала из конечного множества выходных сигналов.

7. Детерминированный конечный автомат (ДКА)-конечный автомат, ни один узел которого не имеет одинаково помеченных дуг, соединяющих его с другими узлами автомата. Задается 5 объектами: М = (К,Т, t, k₁, F), где К - конечное множество состояний автомата ,Т-входной алфавит (множество терминальных символов), t - функция переходов(показывает как ав-т переходит из одного состояния в другое под действием входных символов), k₁-начальное состояние автомата, F- множество конечных состояний.

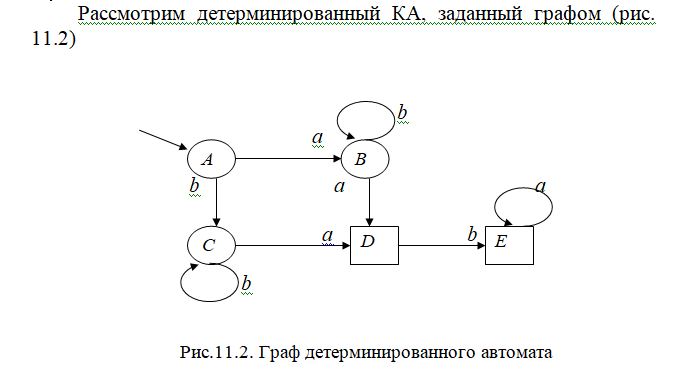
Недетерминированный конечный автомат (НКА) - автомат, в котором есть хотя бы один узел, с исходящими из него дугами, помеченными одинаковыми символами. Следовательно, ф-ция переходов t будет представлять не одно, а множество значений и будет полной.

Продолжение ниже (определение из лекций (то же самое) и граф).

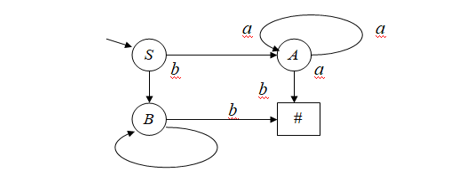
9. Распознователи-это ав-ты, которые имеют т/о два выхода допустить или отвергнуть. Цепочка символов входного алф-та допуск-ся распоз-лем, если под действием этой цепочки ав-т, начавший работу в своем начальном состоянии делает ряд переходов приводящих к выходу допустить, в противном сл-е цепочка отвер-ся. Задача распоз-ля – распознать цепочку входных символов, если она правильная-допустить, если нет –отвергнуть. – Главное определение.

1) Пусть конеч.ав-т обнаруживает слово them.

Эт о ав-т должен иметь 5разл.состояний,каж-е из кот-х предс-т собой позицию в словеthem, эти позиции соответствуют префиксам этого слова от пустой цепочки (никакая позиция в слове еще не достигнута) до целого слова. На каждом шаге читается часть слова. Входным сигналам этого ав-та соотв-ют буквы. Состояние, обозначенное символом Them достигается, когда введено все это слово, т.к.задачей данного ав-та явл-ся распознование именно слова them, то последнее состояние явл-ся единственным допускающим состоянием.

2).МП-ав-ты м/т распозновать различные цепочки символов, напр-р цепочки скобок: когда встреч-ся левая скобка в магазин вталк-ся символ А, правая скобка-символ А вытал-ся из маг-на. Цепочка отвер-ся, если во входной строке остались правые скобки, а магазин уже пуст или если цеп-ка еще не до конца прочитана, а в маг-не есть сим-лы А(т.е.лишние левые скобки). Цеп-ка допуск-ся, если к моменту окончания вход.строки маг-н пуст.

10. Определение со второй картинки*

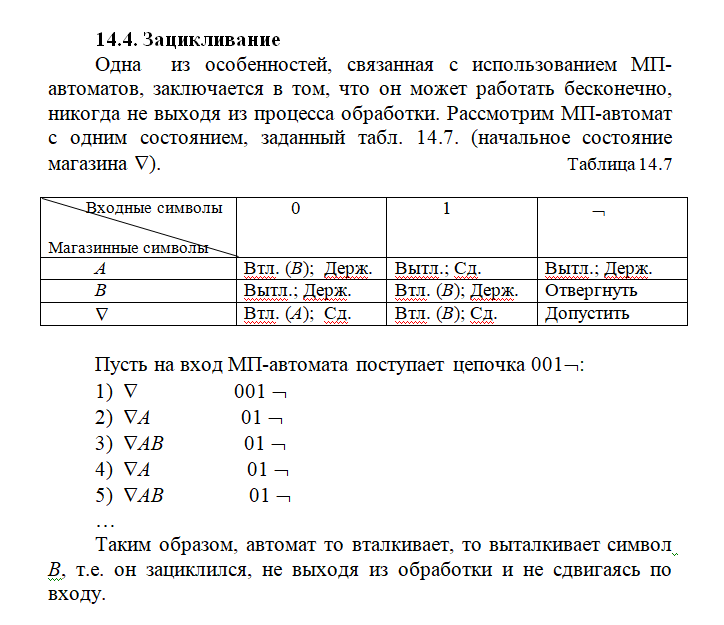
Обработка входной цепочки МП ав-ом(ав-м с Магаз.памятью) как и в сл-е конеч-х ав-ов, осуществляется за ряд мелких шагов.В отличае от кон.ав-та, МП ав-т м/т обрабатывать 1 символ в течение неск-ких шагов. На каж-м шаге управ-щее устр-во МП ав-та принимает решение: закончить ли обр-ку входного символа(и передти к след-му) или продолжить обр-ку текущего.Структура МП ав-та состоит из:

А		0	1	0	1	
В		Входн.строка
С			А	состояние
▼	Магазин

▼-маркер дна магазина, -маркер конца строки.

Сис-ма организации маг-ой п-ти осущес-ся по принципу: LIFO-Last In Fist Out.

Каждый шаг обработки задается правилами(их совокупность наз-т Устр-ом управ-я), использующими инф-цию об: состоянии, верхнем символе маг-на, текущем входном символе.

Переход авт-та в новое состояние вкл-т в себя 3 операции:

1)Операции над магазином:

вталкивание в магазин опред.маг-го символа, выталкивание верхнего сим-ла из маг-на, не изменять магазин.

2)Операции над состоянием:

переход в заданное новое состояние.

3)Операции над входом:

Переход к след-му входному символу(сделать его текущим), не изменять входной сим-л(т.е.перейти и держать).

Детермин-й МП ав-т задается 5 объектами:

1)кон.мн-во входных сим-в, включая маркер конца строки.

2)кон.мн-во магаз-х сим-в, вкл-я маркер дна.

3)кон.мн-во состояний, вкл-я начальное

4)управ-щее устр-во(УУ). УУв каж-й комбинации входного сим-ла, состояния и маг-го сим-ла ставит в соотв-е выход или переход. Выход означает завершение работы, переход-выполнение операции над магазином, сост-ем и входом.

5)начальное содержимое маг-на. Если маг-н пуст, то в его верхушке нах-ся маркер дна, в нач.сост-ии в маг-не м/т нах-ся и некот-е маг-нные сим-лы.

Пусть МП ав-ту н/о распознать цепочку скобок.

1)вход-е мн-во { (,),}

2)мн-во маг-х сим-в {A,▼}

3)мн-во сост-й {S}

4)переходы:

(,А,S = втл(А), сост.(S), сдвиг

(,▼,S = втл(А), сост.(S), сдвиг

),А,S = выт, сост.(S), сдвиг

),▼,S = отвергнуть

,А,S = отвергнуть

,▼,S = допустить.

//сост(S)-перейти в сос-е S.

//Сдвиг-текущим станов-ся сл-й сим-л входной строки.

5)начал-е сост-е маг-на ▼

11.

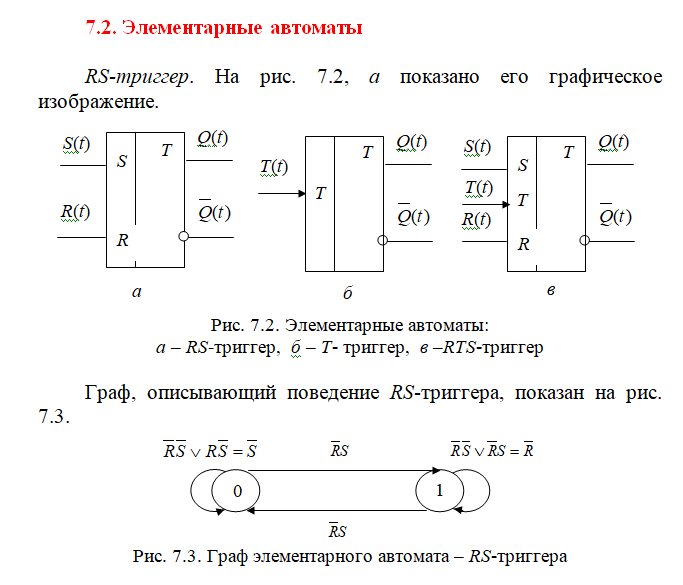
12. Теорема Глушкова (Система элементарных автоматов явлструктурно полнойтогда и только тогда,когда содержит:1)авт-ты Мура,облад полнотой переходов и выходов. 2).комбинацион схему,постороенную на функционал полной системе логических элементов. В этом случае задача структурного синтеза произвольных автоматов сводится к задаче структурного синтеза комбинационных схем).

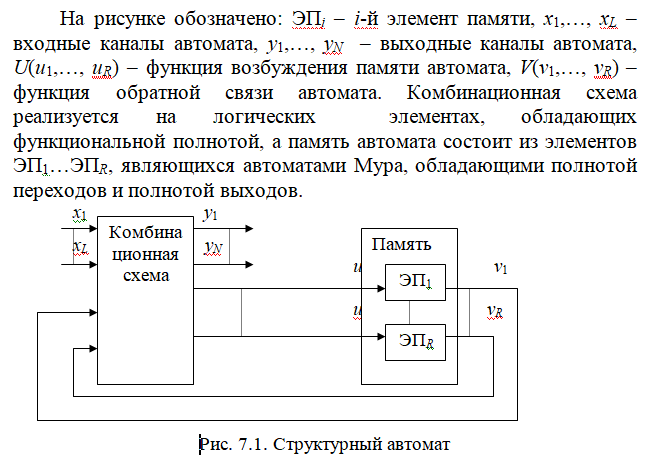
В соответ-ии с теоремой Глушкова задача синтеза структ авт-тасост в построении комбинац части.Математически это записыв-ся так:

y₁=y₁(x₁,x₂,…,x_L,V₁,V₂,…,V_R)…

y_N=y_N(x₁,x₂,…,x_L,V₁,V₂,…V_R)

U₁=U₁(x₁,x₂,…,x_L,V₁,V₂,…V_R)…

U_R=U_R(x₁,x₂,…,x_L,V₁,V₂,…V_R).Т.о.,задача синтеза структурного авт-та сводится к составлению и решению этой сист логических уравнений.

Теоретическим основанием канонического метода структурного синтеза автоматов является теорема о структурной полноте³

Всякая система элементарных автоматов, которая содержит автомат Мура с нетривиальной памятью, обладающий полной системой переходов-выходов и какую-либо функционально полную систему логических элементов, является структурно полной.

Существует общий конструктивный прием (канонический метод структурного синтеза), позволяющий в рассматриваемом случае свести задачу структурного синтеза произвольных автоматов к задаче синтеза комбинационных схем.

+Результатом канонического метода структурного синтеза является система логических уравнений, определяющих выходные сигналы автомата и функции возбуждения элементов памяти. Эти уравнения называются каноническими.

13.

14. Синтез структурного автомата Мура на d -триггерах

Кратко отметим основные этапы синтеза автомата:

1. Находим количество элементов памяти 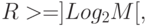  ( М - число состояний абстрактного автомата) и кодируем состояния абстрактного автомата.

2. Кодируем входные и выходные сигналы.

3. Структурный автомат представляем обобщенной схемой.

4. Составляем закодированную таблицу выходов автомата и по ней записываем уравнения выходов.

5. Составляем закодированную таблицу переходов автомата и по ней записываем уравнения для функций возбуждения.

6. Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ} ).

7. Находим количество элементов памяти 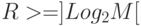 , (   - число состояний абстрактного автомата) и кодируем состояния абстрактного автомата.

8. Кодируем входные и выходные сигналы.

9. Структурный автомат представляем обобщенной схемой.

10. Составление уравнений выходных функций.

Представляем закодированный граф абстрактного автомата, то есть вместо состояний автомата указываются соответствующие кодовые комбинации, а входные сигналы указываются на переходах своими логическими кодовыми комбинациями. Логические кодовые комбинации выходных сигналов 1 рода записываются на переходах, а сигналы 2 рода записываются как метки состояний (или внутри вершины графа). Причем для выходных функций следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения выходов.

11. Составление уравнений функций возбуждения.

На закодированном графе на дугах перехода указываем функции возбуждения, которые соответствуют переключению триггеров, причем следует указывать только те значения функций, которые принимают истинные значения, по которым составляются уравнения функций возбуждения.

12. Уравнения функций возбуждения и выходов минимизируются (по картам Карно, например) и по ним строится схема в заданном функционально - логическом базисе ({И, ИЛИ, НЕ}, {И-НЕ}, {ИЛИ-НЕ} ).

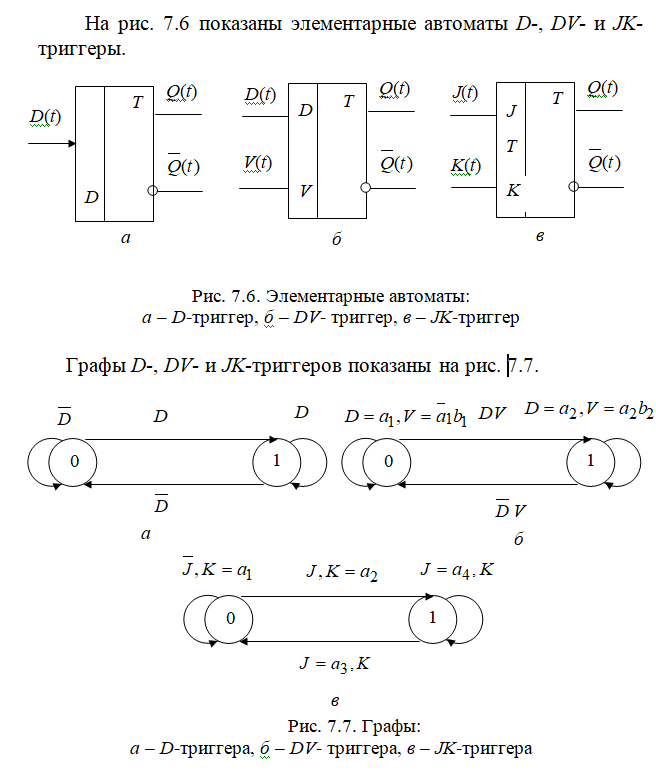
15.

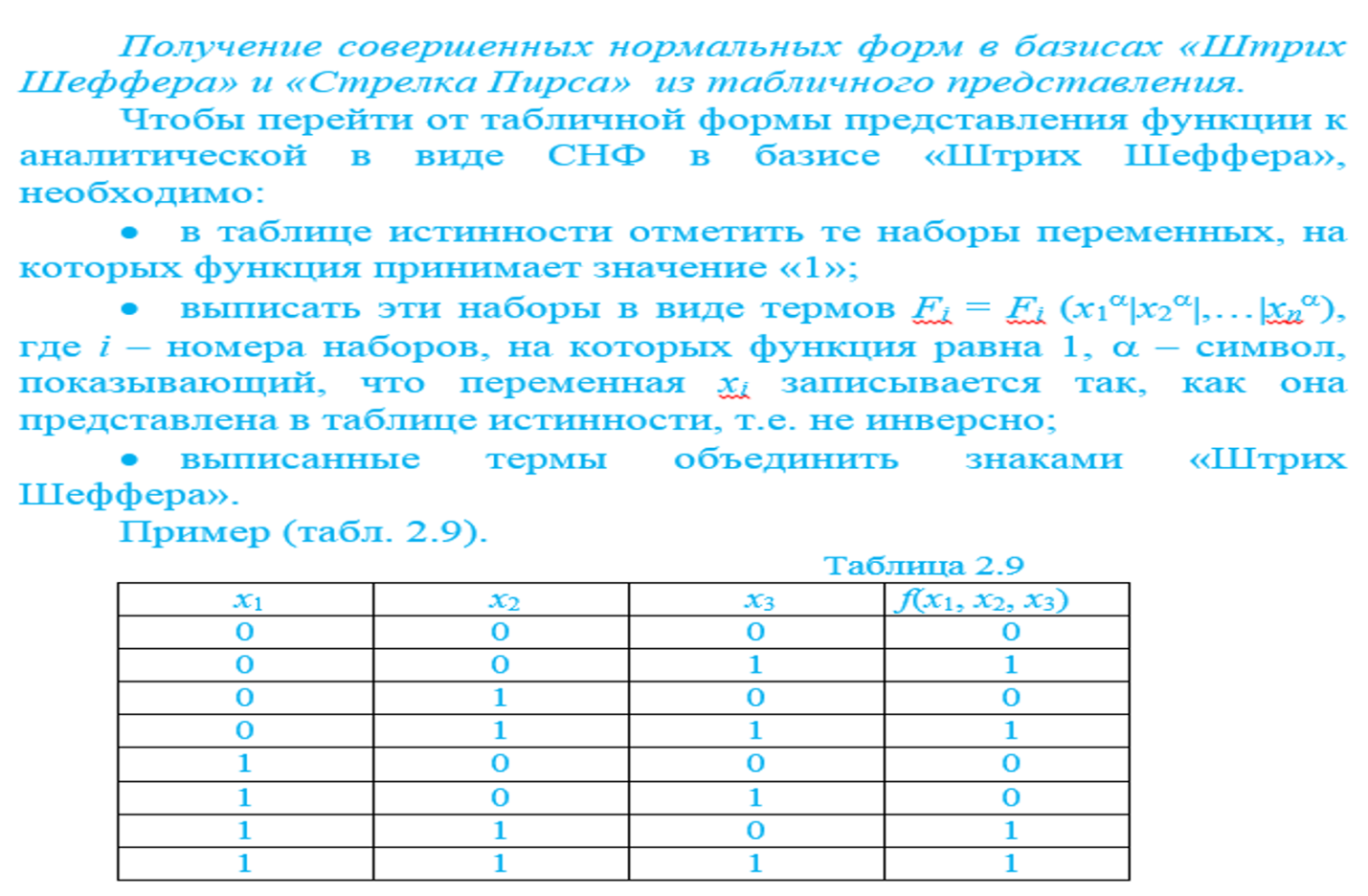
16. (!!!) Схема синтеза графическим методом:

1).строим структурную схему,для чего определяем нужное число элементов памяти,числа входов и выходов структурного авт-та 2).кодирование состояний,входных и выходных каналов структурного авт-та 3).построение закодированного графа авт-та,разметка дуг авт-та 4).получение аналитич-х выражений для сигналов возбуждения(система описывает комбинац часть схемы,описыв управление памятью авт-та) и выходных сигналов авт-та в завис-ти от его внутреннего состояния и действующих входных сигналов 5).минимизация полученных выражений(карты Карно) 6).изображ логической принципиальной схемы структурного авт-та.

Q t	Q t+1	Rt	S
0	0	X	0
0	1	0	1
1	0	1	0
1	1	0	X

Для каждого элементарного автомата схема синтеза имеет свои особенности.Рассмотрим пример синтеза,когда в качестве ЭП выбр RS-триггер.Как видно из табл переходов,чтобы перевести RS-триггер из сост 0 в сост 1 необх на

вход S подать 1,а на вход R подать 0.Чтобы выполн переход из 1 в 0,необх на вход R подать 1,а на вход S подать 0.Зная эти зависим-ти,сформулируем процедуру синтеза структурн авт-та по графу абстракт авт-та. Если при переходе из одного сост в др ЭП_r изменит

своё состояние из 0 в 1,то соответствующая дуга графа отмеч символом S_r.Если переход из 1 в 0,то соответ дуга отмеч символом R_r. Каждой дуге графа будет приписано столько символов S и R,сколько элементарных авт-в изменят своё состояние на переходе,соответ-ему данной дуге.Выражения для S_r и R_r получ-ся как дизъюнкция выражений,каждое из кот-х предст собой конъюнкцию кода состояния,откуда выходит отмеченная соответ-им символом дуга,и входного сигнала,приписанного этой дуге.При синтезе выражений для выходных сигналов y₁,…,y_N необх учитывать синтезируемый авт-т Мура или Мили.Если авт-т Мили,то выходной сигнал y_j получается как дизъюнкция конъюнкций,каждая из кот-х сост из кода состояния,из кот выходит дуга,помеченная y_j и входного сигнала,отмечающего эту же дугу.Если авт-т Мура,то выходные сигналы явл только функциями состояний.

17.

18.