
Лекция 8 Формирование групповых экспертных оценок
.pdf09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
Лекция 8. Методы формирования групповых экспертных оценок
(Подробнее смотрите учебное пособие: Теоретические основы экспертного ранжирования и его применение в медицине и фармации: учебное пособие/ Р.В.Насыров, Г.Я.Ибрагимова, Н.Х.Хафизов, Ю.В.Бойко; Башкирск. гос. медицинск. унив.. Уфа, 2002.- 117 с.)
8.1. Задача группового выбора
При подготовке ответственных решений, основанных на сравнении объектов по качественному признаку, принято опираться на суждения не отдельного эксперта, а экспертной группы. Результатом такого суждения может быть выбор наилучшего объекта из рассматриваемого конечного их множества, определение подмножества лучших объектов, упорядочение всех объектов по степени проявления этого признака. В состав экспертной группы часто включаются специалисты разных направлений, что обеспечивает возможность разностороннего анализа объектов. Коллективное суждение считается более обоснованным, чем индивидуальное.
Коллективный выбор может быть получен либо в результате обсуждения рассматриваемой проблемы экспертной группой и принятия решения путем голосования, либо в результате процедуры, состоящей в том, что каждый член группы независимо от других (т.е. без обязательного обсуждения проблемы со всеми экспертами) делает свой индивидуальный выбор, а затем на основе индивидуальных суждений всех экспертов группы по заранее установленному правилу вырабатывается коллективное суждение. Опыт проведения групповых экспертиз определенно показывает преимущество последнего способа. При совместном обсуждении одни члены группы нередко оказывают влияние на других ее членов. Причиной такого влияния может быть не только убедительная аргументация, но и активность отдельных экспертов, напористость и решительность, с которыми они защищают свою точку зрения. Другой причиной влияния может быть должность эксперта, его ученая степень, его научная или производственная репутация.
Задачу группового выбора в любом случае можно рассматривать как задачу голосования, так как в конечном счете экспертная группа должна выбрать одну альтернативу из нескольких возможных. Если нужно выбрать одну из двух альтернатив, то лучшей считается та из них, .за которую подано больше голосов. Такой выбор представляется справедливым. Если же число альтернатив больше двух, то определение правила справедливого выбора оказываете» далеко не простой задачей.
Рассмотрим в качестве примера получение группового строгого ранжирования на основе индивидуальна строгих ранжирований; здесь под
Теория принятия решений

09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
строгим ранжированием будем понимать линейный строгай порядок. Если такая задача решена, то решена и задача выбора наилучшего объекта либо заданного числа лучших объектов. Пусть три эксперта выполнили ранжирование четырех объектов; экспертные матрицы А1, А2 и А3
представлены на рис. 8.1. Для получения групповой матрицы |
ˆ |
необходимо |
A |
применить некоторое правило агрегирования индивидуальных суждений. Простейшим является правило большинства, когда вопрос о том, является ли объект аi более предпочтительным в групповом упорядочении, чем объект аj, решается большинством голосов (экспертных суждений). Построим групповую матрицу по следующему правилу: при i<j
|
m |
|
|
m |
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
1, если |
|
a k |
|
|
|
|
|
|
|
|
aˆij |
k 1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
aˆ |
|
1; aˆ |
|
0. |
0 востальныхслучаях, aˆ |
ij |
ji |
ii |
|||||||
|
|
|
|
|
|
|
|
|||
где
aˆ |
ij |
|
– элемент групповой матрицы;
a k ij
- элемент индивидуальной
матрицы k-го эксперта; m - число экспертов в группе. Построенная по этому правилу групповая матрица и соответствующий ей граф показаны на том же рисунке. Экспертные матрицы А1, А2, А3 представляют линейные упорядочения, тогда как групповая матрица оказалась нетранзитивной, групповое строгое ранжирование не получено.
|
1 |
1 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
A2 |
A3 |
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
A |
|
|
|
|
Рис. 8.1
Изучение проблем группового выбора составляет содержание отдельной научной дисциплины. Одной из основных задач теории группового выбора является исследование вопроса о том, каким условиям должна отвечать формализованная процедура согласования индивидуальных суждений. Здесь рассматриваются только некоторые применяемые на
Теория принятия решений
09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
практике способы получения группового ранжирования на основе индивидуальных ранжирований экспертов.
8.2. Правила построения группового ранжирования по Борда и по Кондорсе
Различного рода советы и комиссии существуют с очень давних времен. Члены этих советов всегда сталкивались с проблемой выбора, когда число альтернатив было больше двух, однако, насколько известно, какоголибо общепринятого правила группового выбора в таких ситуациях не существовало. Первые формализованные процедуры группового выбора появились только в конце XVIII в. При некоторых видах выборов того времени от избирателя требовалось не указание наиболее предпочтительного для него кандидата, а упорядочение по предпочтительности всех рассматриваемых кандидатов. Авторами первых формализованных процедур группового выбора были французские ученые Борда и Кондорсе. Однако эти процедуры также оказались не без недостатков, поэтому с тех пор было предпринято много попыток создания более совершенных правил группового выбора. С обзорами таких правил можно познакомиться в соответствующей литературе.
Правило упорядочения кандидатов на основе голосов всех избирателей может быть использовано для получения группового ранжирования объектов на основе индивидуальных экспертных ранжирований. Правила группового выбора в дальнейшем рассматриваются применительно к работе экспертной группы. Пусть для примера четыре объекта a1, a2, a3, a4 упорядочены пятью экспертами так, как показано в табл. 8.3.
Таблица 8.3
No |
Экспертные |
|
|
|
Последовательности рангов |
||||||
эксперто |
ранжирования |
|
|
|
|
|
|
||||
|
|
a1 |
a2 |
a3 |
a4 |
||||||
|
|
|
|
|
|
|
|
||||
1 |
a |
a |
3 |
a |
2 |
a |
4 |
1 |
3 |
2 |
4 |
|
1 |
|
|
|
|
|
|
|
|||
2 |
a1 a2 a4 a3 |
1 |
2 |
4 |
3 |
||||||
3 |
a2 a3 a1 a4 |
3 |
1 |
2 |
4 |
||||||
4 |
a2 a4 a3 a1 |
4 |
1 |
3 |
2 |
||||||
5 |
a |
a |
2 |
a |
3 |
a |
4 |
1 |
2 |
3 |
4 |
|
1 |
|
|
|
|
|
|
|
|||
По правилу Борда первое место в групповом ранжировании занимает объект с наименьшей суммой рангов, второе место - объект со следующей наименьшей суммой рангов и т.д. Групповое упорядочение в этом примере имеет вид a2 a1 a3 a4 , лучший объект - a2, хотя в пяти индивидуальных ранжированиях первый объект трижды был на первом месте.
Теория принятия решений

09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
Метод Борда прост и поэтому часто используется на практике. Такую же процедуру получения группового ранжирования предложил в наше время известный английский статистик Кендалл, который, по-видимому, не знал о работе Борда. Применение этого правила вызывает определенные методологические возражения. Обозначим ранг i-го объекта в
индивидуальном ранжировании h-го эксперта через
ih
, ранг этого же
объекта в групповом ранжирования — через
i
. Переходя от сумм рангов к
средним их значениям, получим
|
1 |
2; |
2 |
1,8; |
3 |
2,8; |
4 |
3,4 |
|
|
|
|
|
. Все эти
числа, кроме, возможно, значения
1
2
,
не являются рангами. Не всегда
ясно, как перейти от полученных средних значений к рангам; отношение в рассмотренном примере является верным: a2 a1 , или a2
какое
~ a1 |
? |
Кондорсе предложил другой принцип получения результирующего ранжирования, основанный на учете не рангов объектов, данных экспертами, а результатов их попарных сравнений. Указанные в рассмотренном примере строгие экспертные ранжирования можно представить табл. 8.4, где m1 – число экспертов, высказавшихся за отношение ai a j , m2 – экспертов,
высказавшихся за
a j
ai
, m1+m2=m.
a2 a1
По
a4 |
; |
a |
2 |
|
|
|
большинству голосов имеем: |
a1 a2 |
; |
a1 a3 ; |
a1 a4 |
; a2 |
a3 ; |
||
a3 a4 |
, |
следовательно, групповое |
|
ранжирование имеет |
вид |
|||
a3 a4 , |
|
a1–лучший объект. На |
случай четного |
числа |
экспертов |
|||
можно предусмотреть правило большинства, по которому в результирующее отношение входит отношение из первого столбца таблицы, если m1>m2.
Таблица 8.4
ai a j |
m1 |
a j ai |
m2 |
a |
a |
2 |
3 |
a |
2 |
a |
2 |
1 |
|
|
|
1 |
|
a |
|
a |
3 |
3 |
a |
3 |
a |
|
2 |
|
1 |
|
|
|
1 |
|
|||||
a |
|
a |
4 |
4 |
a |
4 |
a |
|
1 |
|
1 |
|
|
|
1 |
|
|||||
a2 a3 |
4 |
a3 a2 |
1 |
|||||||
a |
2 |
a |
4 |
5 |
a |
4 |
a |
2 |
0 |
|
|
|
|
|
|
|
|
||||
a3 a4 |
3 |
a4 a3 |
2 |
|||||||
Рассмотрим еще один пример, где эксперты представили нестрогие ранжирования тех же объектов, как это показано в табл. 8.5. Групповое
упорядочение по правилу |
Борда дает в этом |
случае |
такую |
же |
последовательность, как и |
в первом примере: |
a2 a1 a3 |
a4 . |
Для |
получения группового упорядочения по правилу Кондорсе нужно построить
Теория принятия решений
09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
табл. 8.6. Из этой таблицы видно, что применение правила абсолютного большинства, как в предыдущем примере, не позволяет получить групповое суждение о некоторых парах объектов.
В этом случае необходимо принять другое правило большинства. Если результатом группового выбора должно быть отношение строгого предпочтения, то следует применить правило относительного большинства: в групповом отношении имеет место ai a j , если т1 т2, при этом значение m3
во внимание не принимается; m1+m2+m3=m. Если же задачей группового выбора является получение отношения нестрогого предпочтения, то правило большинства можно сформулировать так:
а) в групповом отношении ai a j , если т1>т2 и m1+m2+m3=m;
б) в групповом отношении
ai
~
a j
, если т3 т1+т2, либо при т1=т2.
Таблица 8.5
|
|
|
|
No |
|
Экспертные |
|
|
|
|
|
Последовательности рангов |
|
|
||||||||||||||||
|
|
|
|
эксперто |
ранжирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a1 |
|
a2 |
a3 |
|
|
a4 |
|
|
|
|
|
||||||||||||
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a |
|
a |
2 |
~ a |
3 |
a |
4 |
1 |
|
2,5 |
2,5 |
|
|
4 |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
a |
2 |
~ a |
3 |
a |
|
a |
4 |
3 |
|
1,5 |
1,5 |
|
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
a |
2 |
a |
4 |
~ a |
3 |
a |
4 |
|
1 |
2,5 |
|
|
2,5 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
a |
|
a |
3 |
a |
2 |
~ a |
4 |
1 |
|
3,5 |
2 |
|
|
|
3,5 |
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
5 |
|
a |
|
~ a |
2 |
a |
3 |
~ a |
4 |
1,5 |
|
1,5 |
3,5 |
|
|
3,5 |
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 8.6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ai a j |
m1 |
|
|
|
|
|
a j |
ai |
|
m2 |
|
ai ~ a j |
|
m3 |
||||||||||||||||
a |
|
a |
2 |
2 |
|
|
|
|
|
|
a |
2 |
a |
|
|
2 |
|
|
a |
|
~ a |
2 |
|
|
1 |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||
a |
|
a |
3 |
3 |
|
|
|
|
|
|
a |
3 |
a |
|
|
2 |
|
|
a |
|
~ a |
3 |
|
|
0 |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||
a |
|
a |
4 |
4 |
|
|
|
|
|
|
a |
4 |
a |
|
|
1 |
|
|
a |
|
~ a |
4 |
|
|
0 |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||
a |
2 |
a |
3 |
2 |
|
|
|
|
|
|
a |
3 |
a |
2 |
|
1 |
|
|
a |
2 |
~ a |
3 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a2 a4 |
4 |
|
|
|
|
|
|
a4 a2 |
|
0 |
|
|
a2 ~ a4 |
|
1 |
|||||||||||||||
a |
3 |
a |
4 |
3 |
|
|
|
|
|
|
a |
4 |
a |
3 |
|
0 |
|
|
a |
3 |
~ a |
4 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя правило большинства для нестрогих ранжирований применительно к данным табл. 8.6, получим следующие групповые отношения: a1 ~ a2 , a1 a3 , a1 a4 , a2 a3 , a2 a4 , a3 a4 ; они образуют общее упорядочение a1 ~ a2 a3 ~ a4 . Условие транзитивности считается выполненным, если имеет место одна из следующих четырех ситуаций:
1. ai a j и a j ak ai ak ;
Теория принятия решений
09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
2.
a |
i |
a |
j |
|
|
и
a |
j |
~ a |
k |
|
|
ai
ak
;
3. |
ai ~ a j |
и
a |
j |
a |
k |
|
|
ai
ak
;
4. |
ai ~ a j |
и
a |
j |
~ a |
k |
|
|
ai ~ ak .
Обратимся еще к одному примеру упорядочения четырех объектов пятью экспертами, представленному табл. 8.7. Используя правило Борда,
получим групповое упорядочение |
a1 ~ a2 ~ a3 a4 |
; объекты а1; а2; и а3 |
считаются эквивалентными, хотя ни один эксперт так не считает. Чтобы найти групповое упорядочение по правилу Кондорсе, построим табл. 8.8.
Таблица 8.7
No |
Экспертные |
|
|
|
|
|
|
|
|
Последовательности рангов |
||||||||||||||||
эксперто |
ранжирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
a1 |
|
a2 |
|
a3 |
a4 |
|||||||||||||||
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
a |
|
a |
2 |
~ a |
3 |
a |
4 |
|
1 |
|
|
2,5 |
|
2,5 |
4 |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
a |
2 |
~ a |
3 |
a |
|
a |
4 |
|
|
3 |
|
|
1,5 |
|
1,5 |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
a |
2 |
a |
4 |
~ a |
3 |
|
a |
|
4 |
|
|
1 |
|
2,5 |
2,5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
4 |
a |
|
a |
3 |
a |
2 |
~ a |
4 |
|
|
1 |
|
|
3,5 |
|
2 |
3,5 |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 |
a |
|
~ a |
2 |
a |
3 |
~ a |
4 |
|
|
1,5 |
|
1,5 |
|
3,5 |
3,5 |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 8.8 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ai |
a j |
|
|
|
m1 |
|
|
|
a j |
ai |
|
m2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
|
a |
2 |
|
|
|
2 |
|
|
|
a |
2 |
a |
|
|
3 |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
a |
|
a |
3 |
|
|
|
3 |
|
|
|
a |
3 |
a |
|
|
2 |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
a |
|
a |
4 |
|
|
|
3 |
|
|
|
a |
4 |
a |
|
|
2 |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
a |
2 |
a |
3 |
|
|
|
3 |
|
|
|
a |
3 |
a |
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
2 |
a |
4 |
|
|
|
2 |
|
|
|
a |
4 |
a |
2 |
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
3 |
a |
4 |
|
|
|
4 |
|
|
|
a |
4 |
a |
3 |
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
результате |
получим |
следующие групповые |
отношения: |
a1 a3 , |
a1 a4 , a2 |
a3 , a4 |
a2 , a3 a4 , которые |
не образуют |
a2 |
a1 |
, |
общего
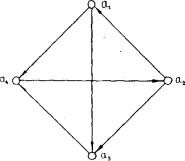
ранжирования. Граф рассматриваемого в примере отношения, который содержит контуры, приведен на рис. 8.2. Возможность противоречивого исхода применения правила большинства была обнаружена еще Кондорсе; такой исход называют парадоксом Кондорсе.
Теория принятия решений
09.03.01 Информатика и вычислительная техника 3 курс ФИРТ УГАТУ
Рис. 8.2
В литературе часто приводится пример вычисления вероятности появления парадокса Кондорсе для случая, когда три эксперта выполняют строгое ранжирование трех объектов. Число возможны?; строгих ранжирований трех объектов равно 6, число различных профилей предпочтения, содержащих такие строгие ранжирования составит 63 =216. Просмотрев все эти комбинации, мы обнаружим ровно 12 случаев противоречивых исходов голосования. Вероятность появления в этом случае парадокса Кондорсе определяется отношением 12:216=0,0555.При большем числе экспертов, равно как и при большем числе альтернатив, содержащих строгие ранжирования, вероятность возникновения парадокса Кондорсе возрастает, что делает этот метод, группового выбора ненадежным.
Заметим, что случай нетранзитивности группового выбора уже был рассмотрен в 8.1.
Теория принятия решений
