ЛР_7

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №7

ПОЗИЦИОННЫЕ ИГРЫ по курсу: ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Санкт-Петербург, 2023г.

Цель работы:

изучить процесс нормализации позиционной игры.

Вариант №8.

Ход работы:

Первый ход делает игрок А: выбирает значение для x из множества {1, 2, 3}.

Второй ход делает игрок В: выбирает значение для y либо из множества {1, 2}.

Третий ход делает игрок А: он помнит и свой первый шаг, и шаг игрока В, поэтому выбор значения для числа z (из множества {1, 2} при x {1, 2, 3}) будет основан на этой информации.

Игрок В имеет следующие стратегии:

В1 − ([1, 1, 1]), В2 − ([2, 2, 2]), В3 − ([1, 1, 2]), В4 − ([1, 2, 1]), В5 − ([1, 2, 2]), В6 − ([2, 1, 2])

В7 − ([2, 2, 1]), В8 − ([2, 1, 1])

Игрок А имеет следующие стратегии:

А1 − (1, [1, 1]), А2 − (1, [1, 2]), А3 − (1, [2, 1]), А4 − (1, [2, 2]),

А5 − (2, [1, 1]), А6 − (2, [1, 2]), А7 − (2, [2, 1]), А8 − (2, [2, 2]),

А9 − (3, [1,1]), А10 − (3, [1, 2]), А11 − (3, [2, 1]), А12 − (3, [2, 2])

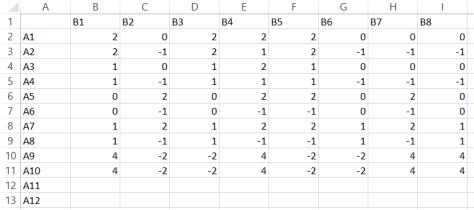
Составляю таблицу выигрышей игрока А и матрицу игры:

Применяем отношения доминирования. Для игрока В исключаются столбцы, все элементы которых больше соответствующих им на данной строке элементов другого столбца. Для игрока А исключаются строки, все элементы которых меньше соответствую-

щим им в данном столбце элементов другой строки.

Сначала убираем строки А11 и А12, так как они меньше строки А7 (рисунок 1).

Рисунок 1 – Убираем меньшие строки для игрока А Далее убираем столбец В1, так как он доминирует над столбцом В3 (рисунок 2).

3

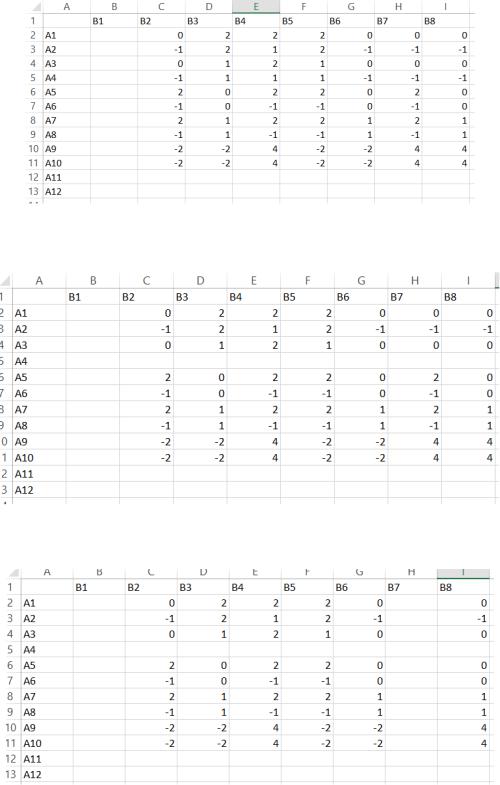
Рисунок 2 -Убираем большие по значению столбцы для игрока В Убираем строку А4, так как она меньше строки А1 (рисунок 3).

Рисунок 3 – Убираем строку А4 для игрока А Далее убираем столбец В7, так как он больше столбца В2 (рисунок 4)

Рисунок 4 – Убираем столбец В7 для игрока В После убрала строку А3, так как она меньше строки А1 (рисунок 5).

4

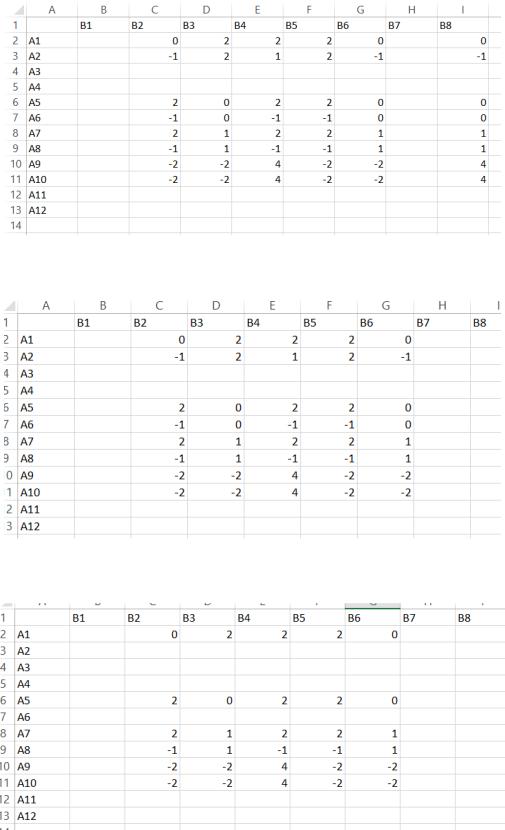
Рисунок 5 – Убираем строку А3 для игрока А Далее убрала столбец В8, так как он больше столбца В6 (рисунок 6).

Рисунок 6 – Убираем столбец В8 для игрока В После убираем строки А2 и А6, так как строка А1 доминирует над ними (рисунок 7).

Рисунок 7 – Убираю строки А2 и А6 для игрока А Далее убрала столбец В3, так как он был больше столбца В6 (рисунок 8).

5

Рисунок 8 – Убираем столбец В3 для игрока В После убрала строки А1 и А5, так как над ними доминирует А7 (рисунок 9).

Рисунок 9 – Убираем строки А1 и А5 для игрока А Далее убрала столбец В4, так как он был доминирующим над В5 и В2, затем убрала

столбец В5, потому что он дублировал столбец В2 (рисунок 10).

Рисунок 10 – Убираем столбцы В4 и В5 для игрока В После убрала строки А8-А10, так как строка А7 доминирует над ними (рисунок 11).

6

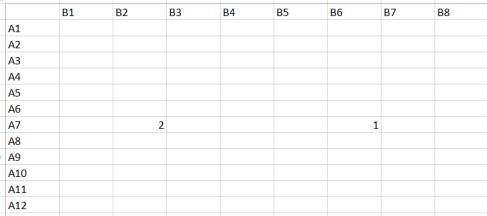
Рисунок 11 – Убираем строки А8-А10 для игрока А Из оставшихся столбцов исключаем В2, так как он доминировал над столбцом В6.

Следовательно, верная стратегия для игрока А – А7, а для игрока В – В6.

Цена игры: v = 1.

Вывод:

В ходе выполнения работы были закреплены навыки нормализации позиционной игры. В результате решения задачи с полной информацией было выявлено, что для игрока А оптимальными является стратегия A7; для игрока B – В6. Таким образом, решение игры

7