ЛР 3 / ЛАБА_3

Цель работы:

Исследование основных характеристик входных потоков заявок, а также базовых принципов моделирования СМО по событиям.

Вариант №9

Порядок эрланговского потока – 1

Параметр

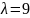
Ход работы:

Результат работы алгоритма в соответствии с рисунком 1.

Рисунок 1 – Вывод значений

Пусть имеется n независимых случайных величин, каждая из которых имеет показательное (экспоненциальное) распределение с одним и тем же параметром лямбда. Тогда сумма этих случайных величин имеет распределение Эрланга. Плотность распределения Эрланга в соответствии с рисунком 2.

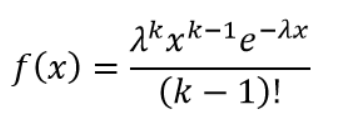
Рисунок 2 – Формула распределения Эрланга

График закона распределения интервалов распределения Эрланга в соответствии с рисунком 3.

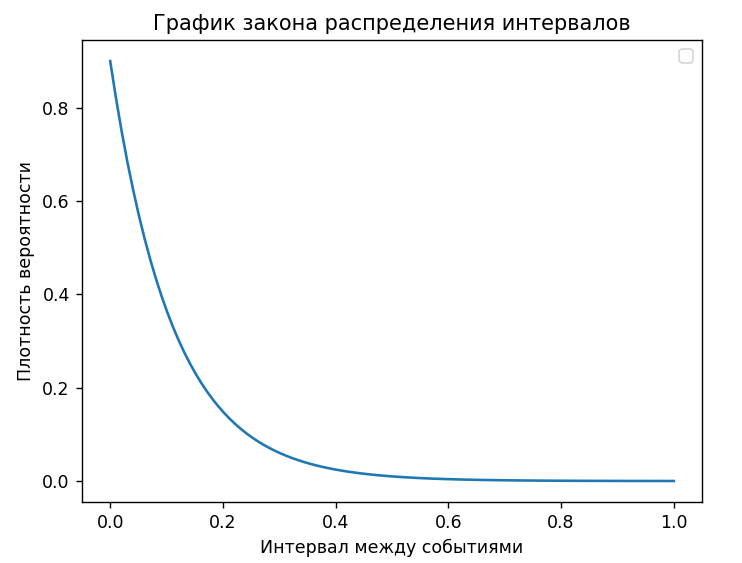
Рисунок 3 – График закона распределения интервалов распределения Эрланга

График зависимости коэффициента вариации в зависимости от размера выборки с теоретическим значением соответствии с рисунком 4 (Листинг A).

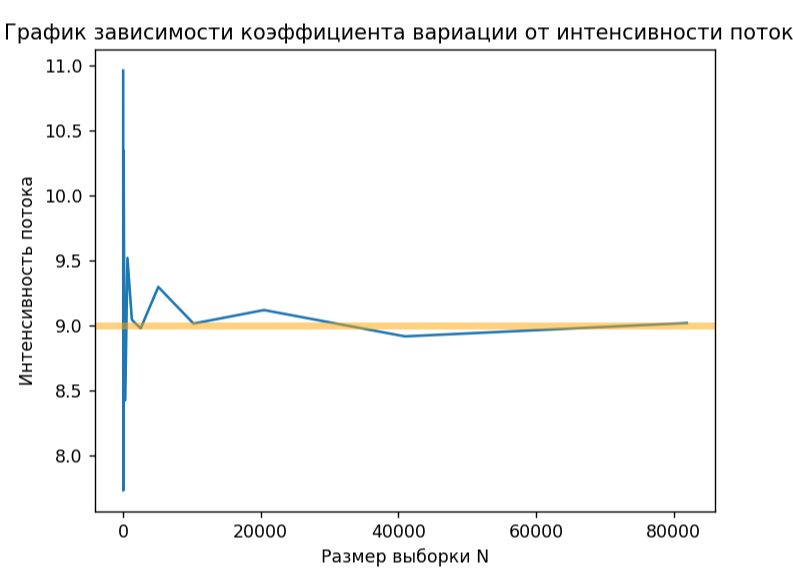
Рисунок 4 – График зависимости коэффициента вариации от размера выборки

График зависимости интенсивности потока от размера выборки с теоретическим значением в соответствии с рисунком 5.

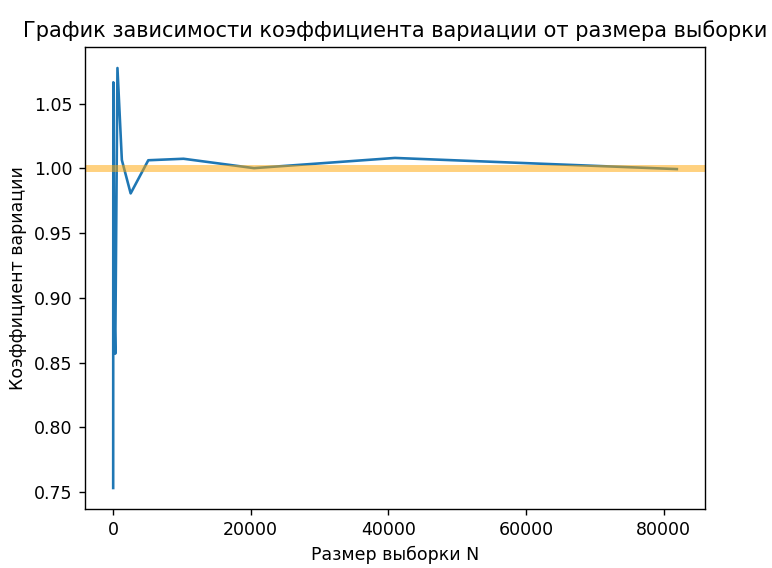
Рисунок 5 – График зависимости интенсивности потока от размера выборки

Список использованных переменных:

Название	Тип переменной	Хранимое значение
mass_N	массив	массив cо значениями размера выборки
mass_lambda	массив	массив со значениями интенсивности потока
mass_v	массив	массив со значениями коэффициента вариации
N	int	стартовое количество поступивших заявок
v_old	float	cтарое значение коэффициента вариации
lamda_old	float	cтарое значение интенсивности потока
k	int	порядок эрланговского потокa
o	int	параметр интенсивности потока
u	массив	случайные числа распределенные по закону Эрланга
Q	float	стандартное отклонение
m	float	мат. ожидание
lamda_new	float	новое значение интенсивности потока
v_new	float	новое значение коэффициента вариации

Вывод:

В ходе работы я исследовала основные характеристики входных потоков заявок, а также базовые принцы моделирования СМО по событиям, построила график закона распределения интервалов, а также график зависимости коэффициента вариации от размера выборки и график зависимости интенсивности потока от размера выборки, добавив на графики теоретические значения.

По полученным графикам можно сделать вывод, что с увеличением выборки значения коэффициента вариации и интенсивности потока приближаются к теоретическим.

Листинг

import numpy as np

import scipy.stats as st

import matplotlib.pyplot as plt

import random

import math

import time

def main():

start_time = time.time()

mass_N = np.array([]) # размер выборки

mass_lambda = np.array([]) # интенсивность потока

mass_v = np.array([]) # коэффициента вариации

N = 10

lamda_old, v_old = 999999, 999999

k = 1 # порядок эрланговского потока

o = 9 # параметр интенсивности потока

scale = 1/o

while True == True:

u = []

for i in range(N):

result = 0

for j in range(k):

result += -math.log(random.random()) * scale

u.append(result)

m = np.mean(u)

Q = np.std(u)

lamda_new = 1/m

v_new = Q/m # коэффициент вариации

if abs((lamda_new - lamda_old)/lamda_old) > 0.01 or abs((v_new - v_old) / v_old) > 0.01:

lamda_old = lamda_new

v_old = v_new

N = 2 * N

else:

lamd = lamda_new

v = v_new

break

mass_N = np.append(mass_N, N)

mass_lambda = np.append(mass_lambda, lamda_new)

mass_v = np.append(mass_v, v_new)

print('Массив значений коэффициента вариации', mass_v)

print('Массив значений интенсивности потока', mass_lambda)

print('Время работы программы:', time.time() - start_time)

# График закона распределения интервала

plt.figure(1)

x = np.linspace(0, 1, 100)

pdf = (pow(o, k) * pow(x, k-1) * np.exp(-o * x)) / math.factorial(k-1)

plt.plot(x, pdf)

plt.title('График закона распределения интервалов')

plt.xlabel('Интервал между событиями')

plt.ylabel('Плотность вероятности')

plt.legend()

plt.show()

# график интенсивности потока

plt.figure(2)

plt.plot(mass_N, mass_lambda)

plt.axhline((1/(k/o)), lw=4, alpha=0.5, color='orange')

plt.title("График зависимости коэффициента вариации от интенсивности потока")

plt.xlabel('Размер выборки N')

plt.ylabel('Интенсивность потока')

plt.show()

# график коэф. вариации

plt.figure(3)

plt.plot(mass_N, mass_v)

plt.axhline(np.sqrt(k / (o ** 2)) / (k / o), lw=4, alpha=0.5, color='orange')

plt.title("График зависимости коэффициента вариации от размера выборки")

plt.xlabel('Размер выборки N')

plt.ylabel('Коэффициент вариации')

plt.show()

main()