ЛР 1 / ЛАБА_1

Цель работы: Изучение метода Монте-Карло, определение точности вычисления определенных интегралов методом Монте-Карло.

Вариант №9.

Ход работы:

Согласно выбранному варианту, необходимо записать математически анализируемую функцию в соответствии с вариантом.

1. 

2. 

3. 

Далее вычисляю определенный интеграл. Проверка полученных значений с помощью встроенных функций в соответствии с рисунком 1 (Листинг A).

Рисунок 1 – Вычисление определенного интеграла

График полученной функции в соответствии с рисунком 2.

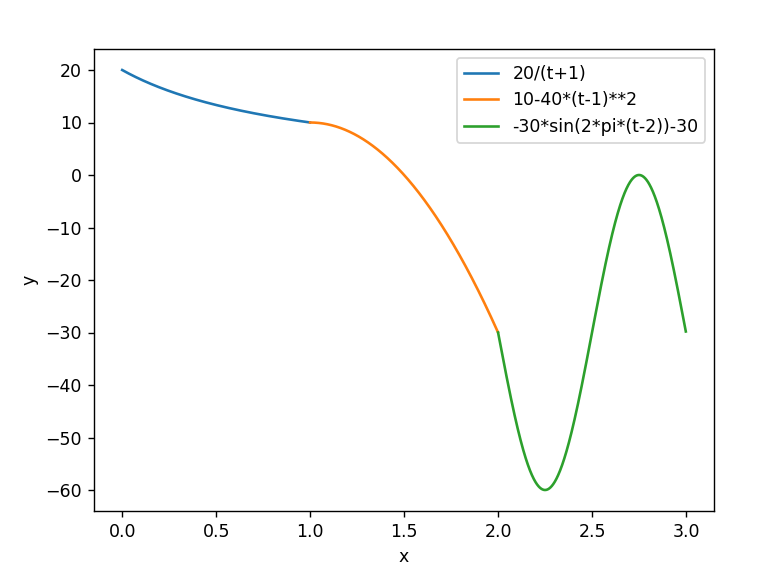
Рисунок 2 – График функции

Разработка программы, вычисляющей величину F методом Монте-Карло при заданном числе экспериментов в соответствии с рисунком 3 (Листинг A).

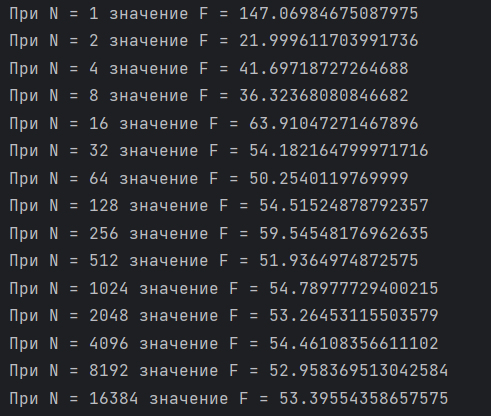
Рисунок 3 – Результаты разработки программы

Список использованных переменных:

Название	Тип переменной	Хранимое значение
all	float	Значение интеграла встроенной функции
x1, x2, x3	float	Случайные значения на заданном промежутке
a, b, c	float	Значение интеграла на каждом промежутке
maccivmass		Массив значений для построения графика функции
mas_x, mas_y		Массив значений кол-ва повторений и значений F
j, k	int	Счетчик цикла
x	float	Случайное значение в заданном промежутке
count	float	Сумма значений от каждой функции
weight	int	Знак функции
n	int	Кол-во повторений цикла
integral_value	float	Значение интеграла сложной функции

График по табличному представлению результатов моделирования количества повторений от значения F в соответствии с рисунком 4.

Рисунок 4 – Полученный график

Вывод:

В ходе работы я познакомилась с методом Монте-Карло, изучила метод для определения точности вычисления определенных интегралов методом Монте-Карло, научилась проверять значения интегралов программным способом. По полученному графику я сделала вывод о том, что между количеством повторений экспериментов и вычислением факториала сложной функции есть прямая зависимость.

Листинг А

from scipy import integrate

from math import *

import numpy as np

import random

import matplotlib.pyplot as plt

global all

all = 0

def punkt1():

global all

def integrals1(t):

return 20/(t+1)

def integrals2(t):

return 10-40*(t-1)**2

def integrals3(t):

return -30*sin(2*pi*(t-2))-30

a = integrate.quad(lambda t: abs(integrals1(t)), 0, 1)[0]

b = integrate.quad(lambda t: abs(integrals2(t)), 1, 2)[0]

c = integrate.quad(lambda t: abs(integrals3(t)), 2, 3)[0]

all = (a + b + c)

print('Значение интеграла встроенной функцией: ', all)

x1 = np.arange(0, 1, 0.001)

x2 = np.arange(1, 2, 0.001)

x3 = np.arange(2, 3, 0.001)

alina = []

for i in x1:

alina.append(integrals3(i))

plt.plot(x1, integrals1(x1), label='20/(t+1)')

plt.plot(x2, integrals2(x2), label='10-40*(t-1)**2')

plt.plot(x3, alina, label='-30*sin(2*pi*(t-2))-30')

plt.xlabel('x')

plt.ylabel('y')

plt.legend()

plt.show()

return all

def monte_karlo():

mas_x = []

mas_y = []

for j in range(0, 15):

n = 2 ** j

count = 0

for i in range(0, n):

t = random.uniform(0.0, 3.0)

weight = 1

if t < 1:

count += abs(20/(t+1))

if 1 <= t <= 2:

count += abs(10-40*(t-1)**2)

if t > 2:

count += abs(-30*sin(2*pi*(t-2))-30)

if t < 1 or t > 2:

weight = -weight

integral_value = (3.0/n) * count

print('При N =', n, 'значение F =', integral_value)

mas_x.append(n)

mas_y.append(integral_value)

fig, ax = plt.subplots()

ax.hlines(all, -5, 10000, color = 'blue')

plt.plot(mas_x, mas_y)

plt.legend(['истинное значение F'])

plt.semilogx(basey=2)

ax.set_xlabel('N повторений')

ax.set_ylabel('значение F')

plt.show()

if __name__ == '__main__':

punkt1()

monte_karlo()