
Лаба 3
.docx
Цель: изучить различную организацию синхронных триггерных схем; овладеть методом логического проектирования синхронного двухступенчатого триггера; получить навыки проектирования синхронных триггерных схем на VHDL; приобрести опыт экспериментального исследования заданного типа триггера.
Задание. Дана таблицы переходов и уравнения, описывающие логическую структуру триггера:
Таблица переходов |
||
E1(t) |
E2(t) |
Q(t+1) |
0 0 1 1 |
0 1 0 1 |
Q(t) 1 0 0 |
Требуется:
Провести синтез логической структуры синхронного двухступенчатого триггера (E1E2-триггер);
Провести синтез логической структуры синхронного триггера с динамическим управлением записью (DV-триггер и JK-триггер);
Построить временные диаграммы спроектированных триггеров;
Описать триггер на VHDL;
Разработать схему исследования спроектированных триггеров с использованием макроэлементов стенда и осциллографа;
Получить результаты экспериментальных исследований.
Напишем таблицу состояний и матрицу переходов E1E2-триггера.
Таблица 1. Таблица состояний E1E2-триггера |
|
|
Таблица 2. Матрица переходов E1E2-триггера |
|||||||
|
|
Q(t+1) |
|
|
|
|
|
|||
0 |
0 |
x |
|
|
|
1 |
x |
|||
0 |
1 |
0 |
|
|
|
0 |
1 |
|||
1 |
0 |
1 |
|
|
|
1 |
0 |
|||
1 |
1 |
Q(t) |
|
|
|
x |
1 |
|||
Построим таблицу истинности, исходя из задания и таблицы 2.
Таблица 3. Таблица истинности функций возбуждения.
№ |
C |
E1 |
E2 |
Q(t) |
F1( ) |
F2( ) |
Q(t+1) |
|
0 |
0 |
0 |
0 |
0 |
1 |
x |
Q(t) |
|
1 |
0 |
0 |
0 |
1 |
x |
1 |
|
|
2 |
0 |
0 |
1 |
0 |
1 |
x |
Q(t) |
|
3 |
0 |
0 |
1 |
1 |
x |
1 |
|
|
4 |
0 |
1 |
0 |
0 |
1 |
x |
Q(t) |
|
5 |
0 |
1 |
0 |
1 |
x |
1 |
|
|
6 |
0 |
1 |
1 |
0 |
1 |
x |
Q(t) |
|
7 |
0 |
1 |
1 |
1 |
x |
1 |
|
|
8 |
1 |
0 |
0 |
0 |
1 |
x |
Q(t) |
|
9 |
1 |
0 |
0 |
1 |
x |
1 |
|
|
10 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
11 |
1 |
0 |
1 |
1 |
x |
1 |
|
|
12 |
1 |
1 |
0 |
0 |
1 |
x |
0 |
|
13 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|
14 |
1 |
1 |
1 |
0 |
1 |
x |
0 |
|
15 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Найдем минимальную ДНФ для функций F1 и F2 с помощью диаграмм Вейча.


Диаграммы Вейча функций возбуждения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
12 |
13 |
9 |
8 |
|
|
|
1 |
1 |
|
1 |
|
|
|
|
0 |
|
x |
|
||||||||||||||||||||||||||
14 |
15 |
11 |
10 |
|
|
1 |
1 |
x |
0 |
|
|
x |
0 |
1 |
1 |
|
|||||||||||||||||||||||||||||
|
6 |
7 |
3 |
2 |
|
|
1 |
|
x |
1 |
|
|
x |
1 |
1 |
x |
|||||||||||||||||||||||||||||
4 |
5 |
1 |
0 |
|
|
1 |
x |
X |
1 |
|
|
x |
1 |
1 |
x |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Эталонная диаграмма |
Диаграмма F1 |
Диаграмма F2 |
|||||||||||||||||||||||||||||||||||||||||||
Выпишем минимальные ДНФ функций:
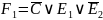
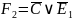
Представим функции в базисе «Штрих Шеффера»:
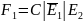
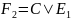
Построим схему спроектированного E1E2-триггера на базе элементов «И-НЕ» с асинхронными входами и предварительной установки триггера в состояние 0 или 1 соответственно (рисунок 1).
Параметры временной диаграммы работы синхронного двухступенчатого E1E2-триггера (представлена на рисунке 2):
Задержка переключения сигнала из 1 в 0: 2 нс.
Задержка переключения сигнала из 0 в 1: 3 нс.
Длительность асинхронной установки в 1 или 0: 5 нс.
Длительность синхросигнала: 7 нс
Длительность сигнала после окончания синхросигнала: 10 нс
Одна клетка равна 1 нс.
Задержка
переключения выходного сигнала из 1 в
0:
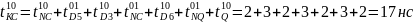
Задержка
переключения выходного сигнала из 0 в
1:
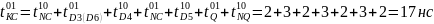
Напишем таблицу состояний и матрицу переходов DV-триггера.
Таблица 4. Таблица состояний DV-триггера |
|
|
Таблица 5. Матрица переходов DV-триггера |
|||||||
D |
V |
Q(t+1) |
|
|
|
D |
V |
|||
0 |
0 |
Q(t) |
|
|
|
|
|
|||
0 |
1 |
0 |
|
|
|
1 |
1 |
|||
1 |
0 |
Q(t) |
|
|
|
0 |
1 |
|||
1 |
1 |
1 |
|
|
|
|
|
|||
Построим таблицу истинности, исходя из задания и таблицы 5.
Таблица 6. Таблица истинности функций возбуждения.
№ |
E1 |
E2 |
Q(t) |
F1( |
F2( |
Q(t+1) |
|
0 |
0 |
0 |
0 |
|
|
Q(t) |
|
1 |
0 |
0 |
1 |
|
|
|
|
2 |
0 |
1 |
0 |
1 |
1 |
1 |
|
3 |
0 |
1 |
1 |
|
|
|
|
4 |
1 |
0 |
0 |
|
|
0 |
|
5 |
1 |
0 |
1 |
0 |
1 |
|
|
6 |
1 |
1 |
0 |
|
|
0 |
|
7 |
1 |
1 |
1 |
0 |
1 |
|
Найдем минимальную ДНФ для функций F1 и F2 с помощью диаграмм Вейча.
Диаграммы Вейча функций возбуждения:
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
6 |
7 |
5 |
4 |
|
|
|
0 |
0 |
|
|
|
|
1 |
1 |
|
|
||||||||||||
|
2 |
3 |
1 |
0 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Эталонная диаграмма |
Диаграмма F1 |
Диаграмма F2 |
|||||||||||||||||||||||||||
Зададим такие значения неизвестных переменных ai и bi, чтобы функция F2 (V) принимала единичное значение.

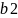 =
1
=
1
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
0 |
0 |
|
|
1 |
|
1 |
1 |
|
|||||
|
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
Диаграмма F1 |
Диаграмма F2 |
|||||||||||||||
Выпишем минимальные ДНФ функций:

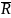
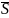
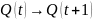
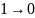
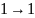
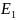
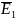
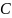
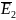
 x
x x
x 1
1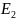
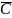
 x
x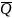
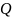
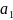
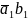
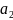
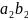
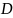 )
)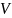 )
) 0
0 1
1 0
0