
Отчет по практике
.docxИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
на прохождение практики обучающегося направления подготовки/ специальности
1. Фамилия, имя, отчество обучающегося:
3. Тема индивидуального задания: Применение теории алгоритмов для решения математических и логических задач. 4. Исходные данные: 7 8 2 1 4 5.
Содержание отчетной документации:
6.1. индивидуальное задание; 6.2. отчёт, включающий в себя:
−титульный лист;
− материалы о выполнении индивидуального задания (содержание определяется кафедрой);
− выводы по результатам практики;
− список использованных источников.
6.3. отзыв руководителя от профильной организации (при прохождении практики в профильной организации).
Срок представления отчета на кафедру: «___»______________ 2020 г.
Руководитель практики
должность, уч. степень, звание подпись, дата
СОГЛАСОВАНО Руководитель практики от профильной организации |
инициалы, фамилия
|
должность подпись, дата
Задание принял к исполнению: Обучающийся |
инициалы, фамилия
|
дата подпись |
инициалы, фамилия |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«Санкт–Петербургский государственный университет аэрокосмического приборостроения»
Кафедра №41 Вычислительных систем и программирования
ОТЧЁТ ПО ПРАКТИКЕ
ЗАЩИЩЁН С ОЦЕНКОЙ
РУКОВОДИТЕЛЬ

должность, уч. степень, звание подпись, дата инициалы, фамилия
ОТЧЁТ ПО ПРАКТИКЕ


выполнен Пирожниковой Наталией Фёдоровной

фамилия, имя, отчество обучающегося в творительном падеже
по направлению подготовки 09.03.03

код наименование направления

наименование направления
направленности
код наименование направленности
наименование направленности
z94
Обучающийся группы № 11

номе подпись, дата инициалы, фамилия
Варианты заданий: 7 8 2 1 4;
Задание 1 Вариант 7.
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, во второй – 3 камня. У каждого игрока неограниченное количество камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает число камней в какой-то кучке в 3 раза, или добавляет 3 камня в любую из кучек. Выигрывает игрок, после хода которого общее число камней в двух кучках становится не менее 33. Кто выигрывает: игрок, делающий ход первым, или игрок, делающий ход вторым? Ответ обоснуйте.
Решение:
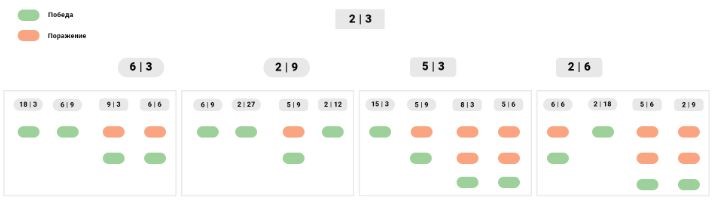
По схеме видно, что выигрыш возможен на 3-м ходе (1 игроком), но при любом первом ходе, второй игрок, просчитав варианты, может привести себя к победе.
Ответ: выигрывает 2-ой игрок при грамотном расчёте ходов.
Задание 4 Вариант 1.
Определить, сколько единиц в двоичной записи произвольного десятичного числа А (100<A<1000).
Решение:
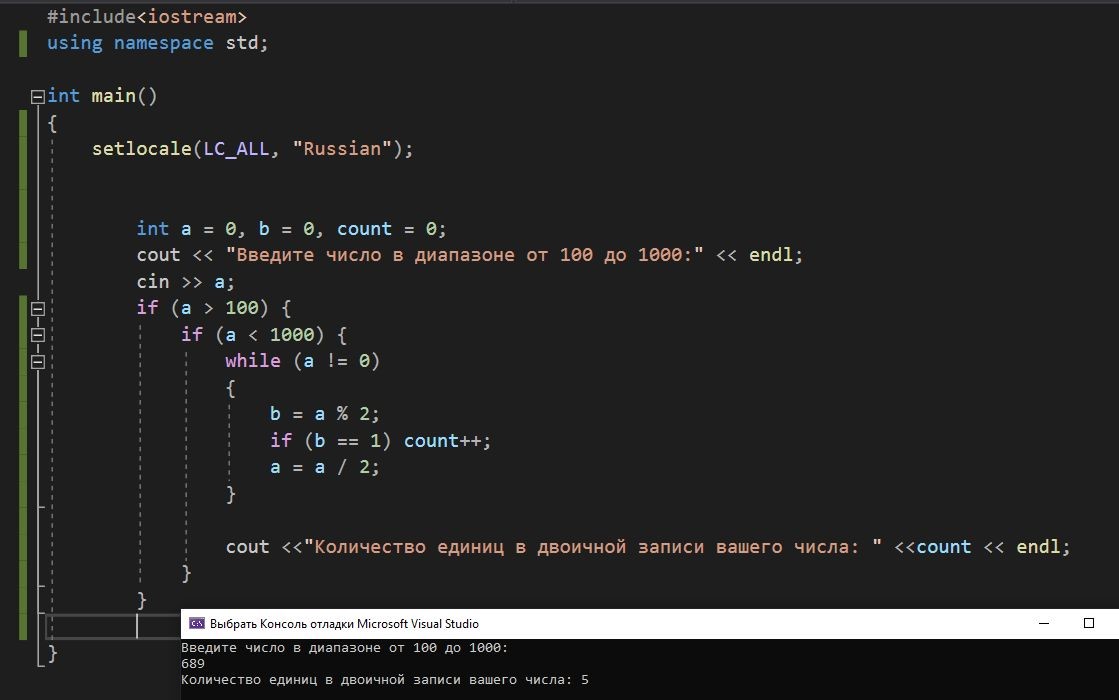
Задание 5 Вариант 4.
Четыре подруги – Маша, Полина, Ольга и Наташа – участвовали в соревнованиях по бегу и заняли четыре первые места.
Установите, кто какое место занял, если известно, что в каждом из приведенных ниже ответов, которые дали лукавые девушки опоздавшему на финиш корреспонденту, верной является лишь половина. Наташа: «Ольга была второй, а Полина – первой». Маша: «Нет, Ольга была первой, а второй была ты». Ольга: «Да, что вы, девочки! Маша была третьей, а Полина прибежала четвёртой».
|
Истина |
|
Ложь |
предположение.
|
Маша |
Полина |
Оля |
Наташа |
Маша |
|
|
3 |
|
Полина |
|
|
4 |

1 |
Оля |
1 |
|
|
2 |
Наташа |
2 |
|
|
|
Оля и Наташа не могут обе быть первыми. Неверное предположение.
Выяснили: Наташа 2. Оля не 1 и не 2.
предположение.
|
Маша |
Полина |
Оля |
Наташа |
Маша |
|
|
3 |
|
Полина |
|
|
4 |
1 |
Оля |
1 |
|
|
2 |
Наташа |
2 |
|
|
|
Полина 1, Наташа 2. Оля не 1 и не 2. Верное предположение.
предположение.
|
Маша |
Полина |
Оля |
Наташа |
Маша |
|
|
3 |
|
Полина |
|
|
4 |
1 |
Оля |
1 |
|
|
2 |
Наташа |
2 |
|
|
|
Полина не может быть и 1 и 4. Неверное предположение.
предположение.
|
Маша |
Полина |
Оля |
Наташа |
Маша |
|
|
3 |
|
Полина |
|
|
4 |
1 |
Оля |
1 |
|
|
2 |
Наташа |
2 |
|
|
|
Верное предположение.
Ответ: Полина 1, Наташа 2, Маша 3, Оля 4.
Вывод: я освоила и усовершенствовала решение задач из теории игр и алгебры логики.
