Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач

2.1. Частные производные функции двух переменных

Переменная z называется функцией двух независимых переменных х и у на некотором множестве точек , если каждой паре значений из множества соответствует определенное значение величины z.

Пишут:

.

С геометрической точки зрения функция представляет собой поверхность.

Если при отношение частного приращения функции к вызвавшему его приращению аргумента имеет конечный предел, то этот предел называется частной производной функции по независимой переменной х в точке и обозначается , или , или .

Таким образом, по определению

.

Аналогично,

.

Так как вычисляется при неизменном значении переменной у, а – при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции называется ее производная по у, вычисленная в предположении, что х – постоянная.

Пример 1

Найти частные производные функции .

Решение

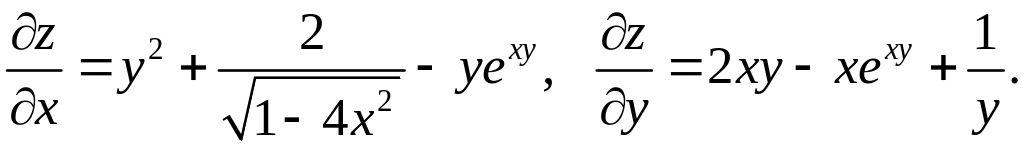
Пример 2

Показать, что функция удовлетворяет уравнению .

Решение

Найдем частные производные

,

.

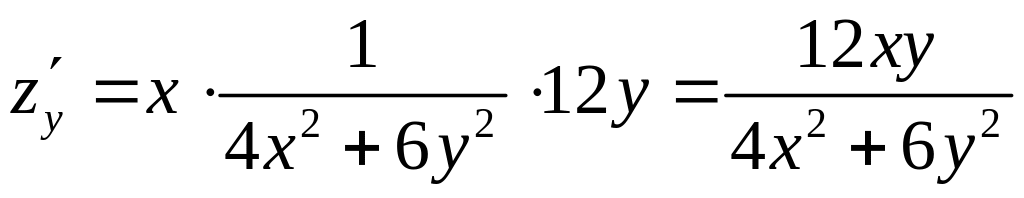Подставим найденные выражения в левую часть уравнения:

что и требовалось доказать.

2.2. Дифференциал функции двух переменных

Частным дифференциалом функции называется произведение частной производной на соответствующее произвольное приращение независимой переменной:

выражение называется частным дифференциалом функции по переменной х;

выражение называется частным дифференциалом функции по переменной у.

Пример 1

Найти частные дифференциалы функции

Решение

, .

Полный дифференциал функции равен сумме ее частных дифференциалов:

.

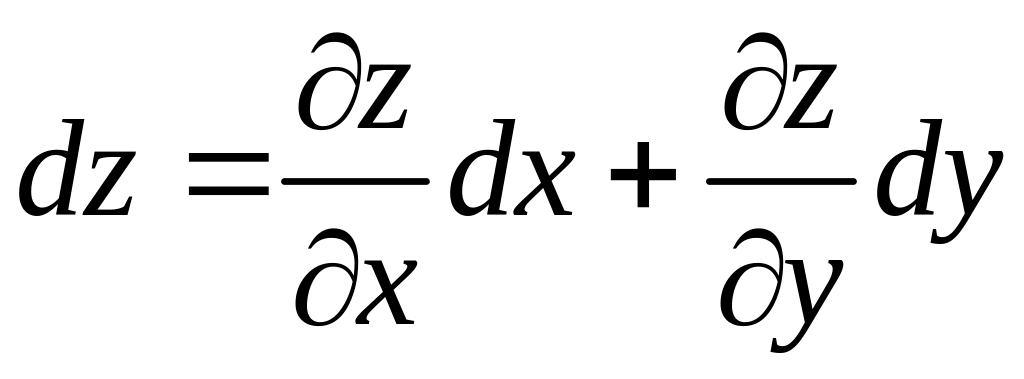Пример 2

Найти дифференциал функции .

Решение

Найдем частные производные

,

.

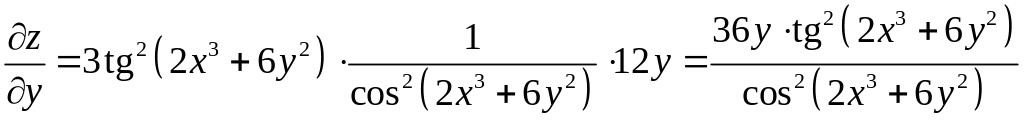Подставим частные производные в формулу полного дифференциала, получим

.

2.3. Касательная плоскость и нормаль к поверхности

Прямая линия называется касательной к поверхности в некоторой точке , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку .

Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку , называется касательной плоскостью к поверхности в точке .

Если уравнение поверхности задано неявно, т.е. , то уравнение касательной плоскости к поверхности в точке имеет вид

Если уравнение поверхности задано в явном виде, т.е. , то уравнение касательной плоскости к поверхности имеет вид

.

Нормалью к поверхности называют прямую, перпендикулярную к касательной плоскости в точке касания.

Если уравнение поверхности задано неявно, т.е. , то уравнение нормали к поверхности в точке имеет вид

.

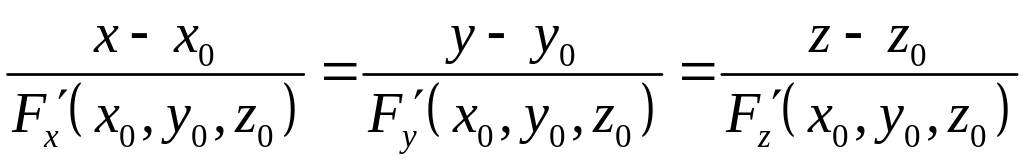Если уравнение поверхности задано в явном виде, т.е. , то уравнение нормали имеет вид

.

Пример

Составить уравнения касательной плоскости и нормали к поверхности в точке .

Решение

Найдем частные производные и вычислим их значения в точке :

.

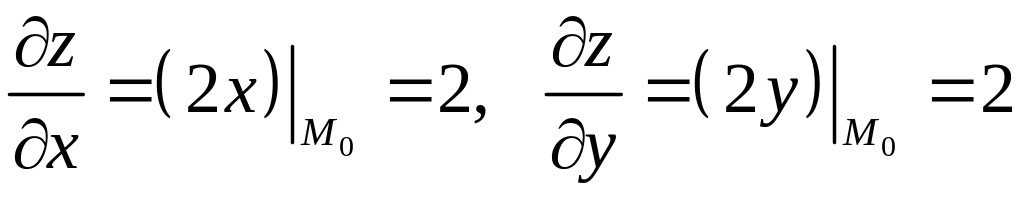Уравнение касательной плоскости:

или .

Уравнение нормали:

.