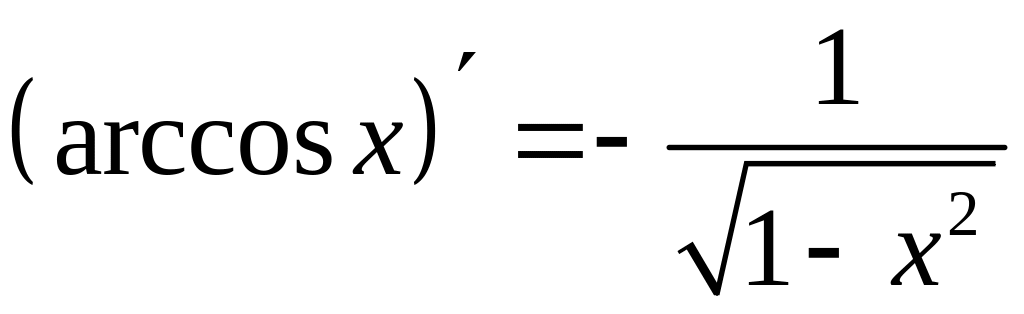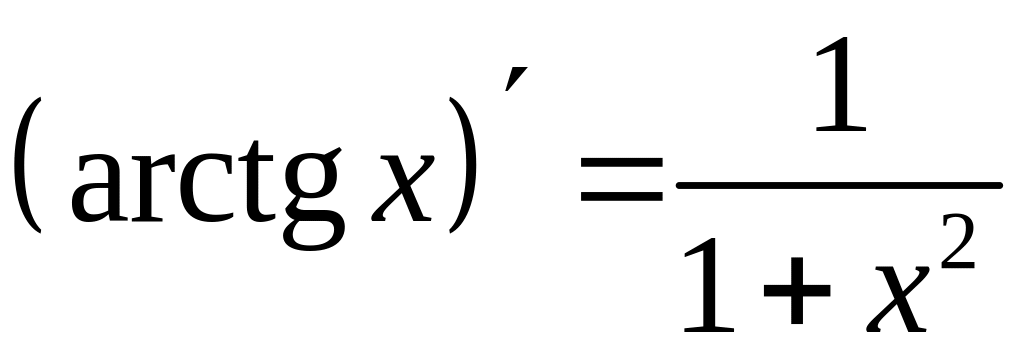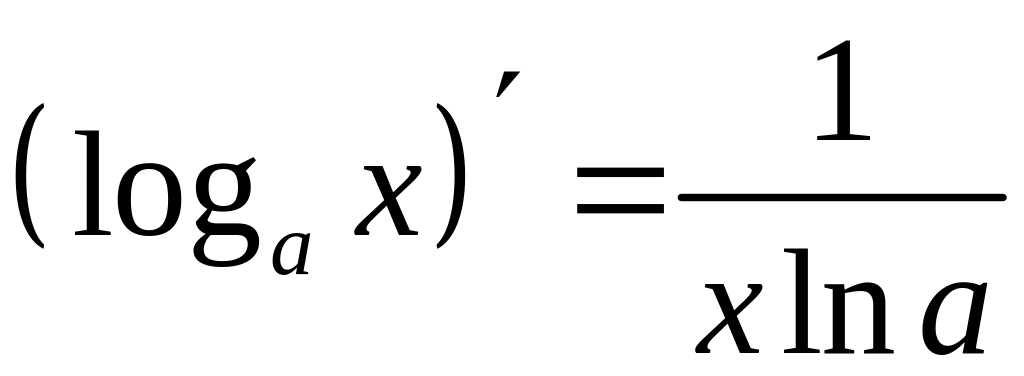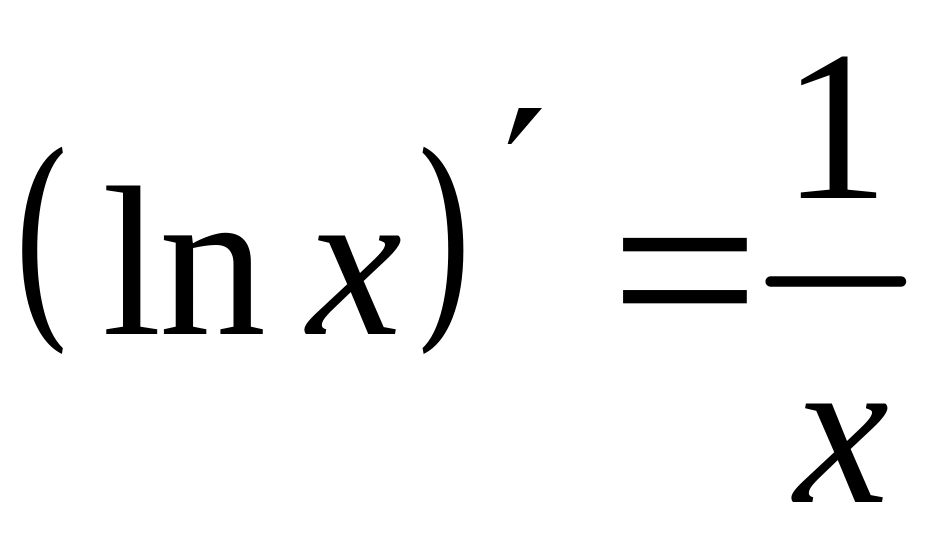Классификация точек разрыва

Определение. Если в точке функция имеет пределы слева и справа и они равны между собой, а в точке

или функция не определена, то точка называется точкой устранимого разрыва функции .

В этом случае функцию можно доопределить в точке так, чтобы она стала непрерывной, т.е. положить

.

Определение. Если в точке функция имеет конечные пределы слева и справа, причем , то точка называется точкой разрыва функции 1-го рода.

При переходе через точку значение функции претерпевает скачок, измеряемый разностью .

Определение. Точка называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен .

Пример

В точках и для функции 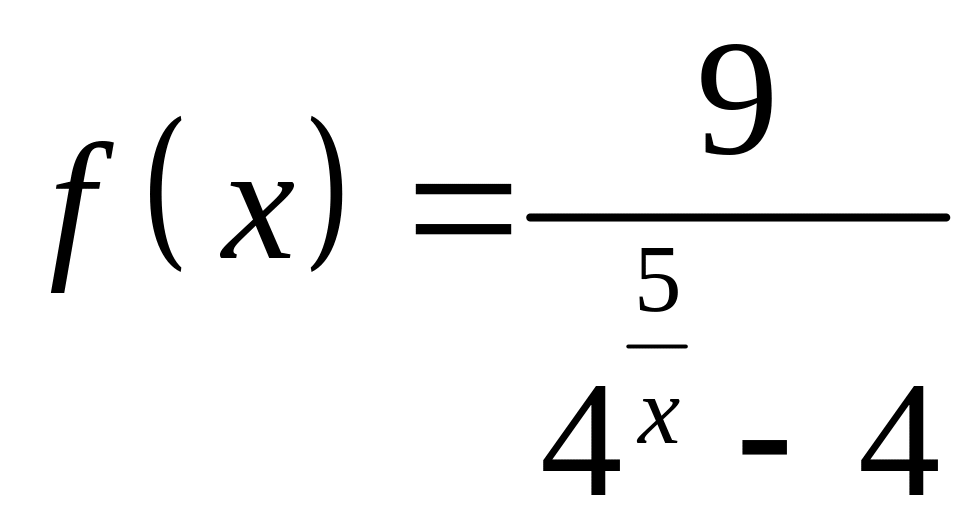установить характер точек разрыва.

Решение

Область определения функции . Данная функция непрерывна во всех точках, кроме точек и , которые не входят в область определения функции.

Исследуем точку , находя ее односторонние пределы в этой точке:

если , то , тогда предел слева ,

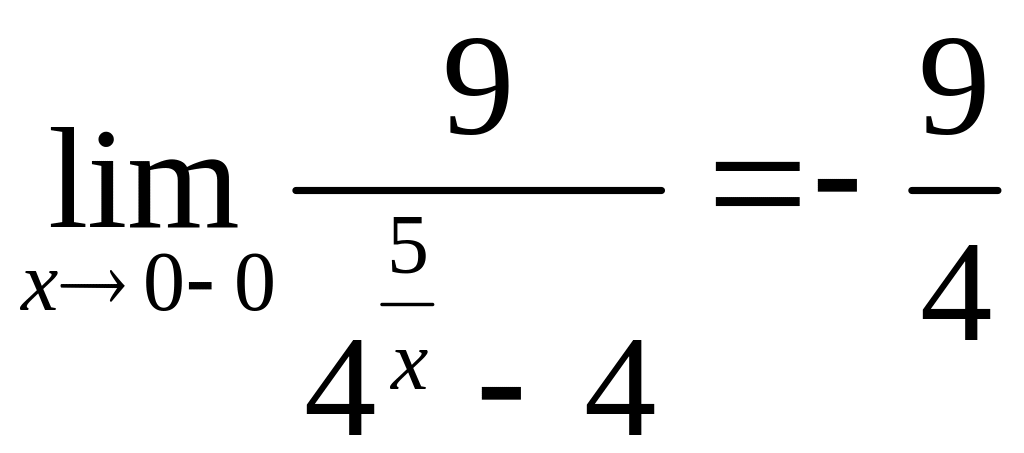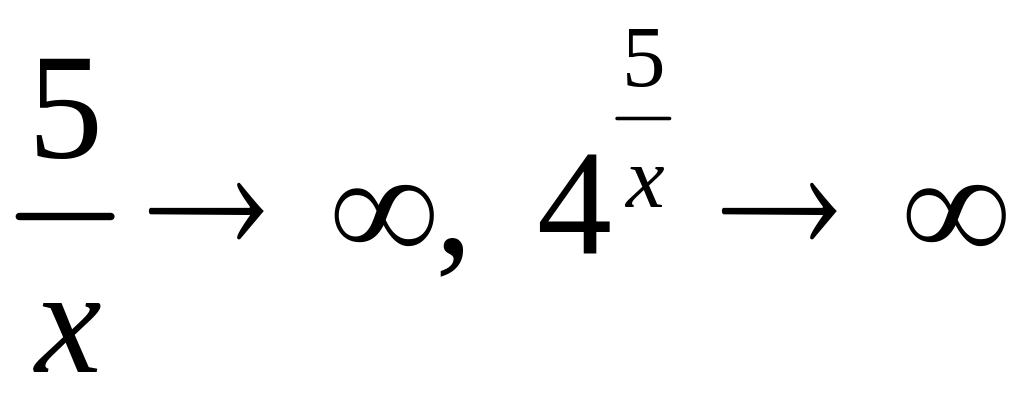если , то , тогда предел справа .

Так как односторонние пределы конечны, но не равны между собой, то в точке функция имеет разрыв 1-го рода (скачок функции).

Исследуем точку , находя ее односторонние пределы в этой точке:

если , то , тогда ,

если , то , тогда .

Так как односторонние пределы равны , то в точке функция имеет разрыв 2-го рода.

1.5. Правила дифференцирования

Определение. Производной функции в данной точке х называется предел отношения приращения функции к приращению аргумента, при , если он существует.

По определению

.

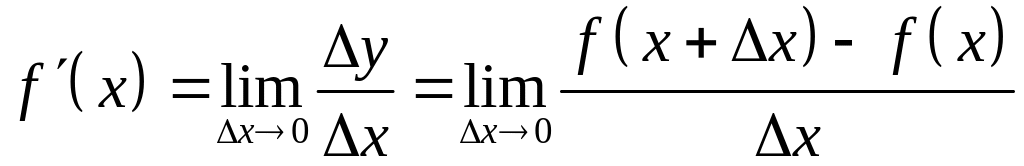Таблица производных

№		№
1	,	10
2		11
3		12
4		13
5		14
6		15
7		16
8		17
9		18

Правила дифференцирования

1. Производная постоянной равна нулю: .

2.

Теорема. Если каждая из функций и дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии ) так же дифференцируемы в этой точке, причем имеют место формулы:

1) ,

2) ,

3) .

Следствие. Постоянный множитель можно выносить за знак производной:

.

Пример

Используя таблицу производных и правила дифференцирования, найти производную функции .

Решение

1.6. Производная сложной функции

Пусть дана сложная функция где или .

Теорема. Если функция дифференцируема в точке , а функция дифференцируема в точке , тогда сложная функция дифференцируема в точке , причем

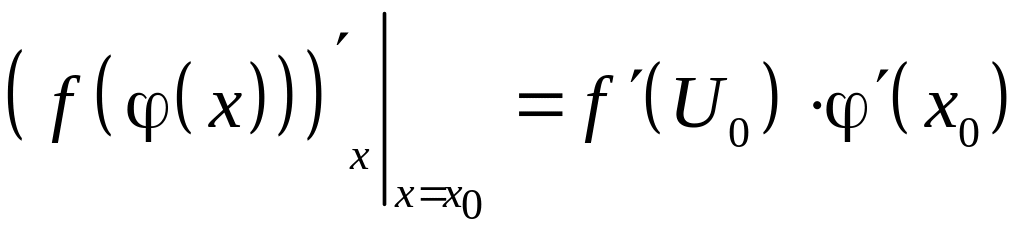или

Замечание. Теорема может быть обобщена на случай любой конечной цепочки функций. Так, если , или и существуют производные , то .

Пример

Найти производную функции .

Решение

Здесь ,

, тогда .