2.8. Ряды Тейлора и Маклорена
Пусть функция бесконечное число раз дифференцируема в окрестности некоторой точки и пусть ее можно представить в виде суммы степенного ряда, сходящегося в интервале, содержащем точку .
Ряд вида
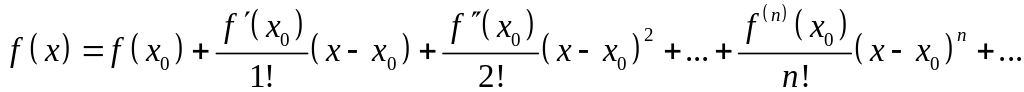
называется
рядом
Тейлора
для функции
,
а коэффициенты ряда
называются коэффициентами
Тейлора.
Говорят,
что функция
разложена в степенной ряд по степеням
в окрестности точки
.
В
частности, при
,
ряд вида
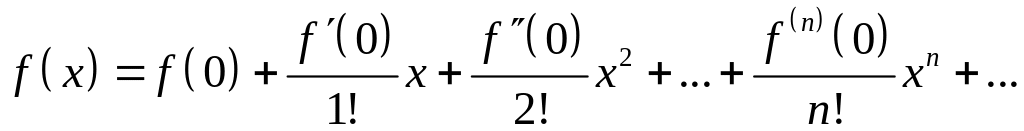
называется
рядом
Маклорена,
а коэффициенты
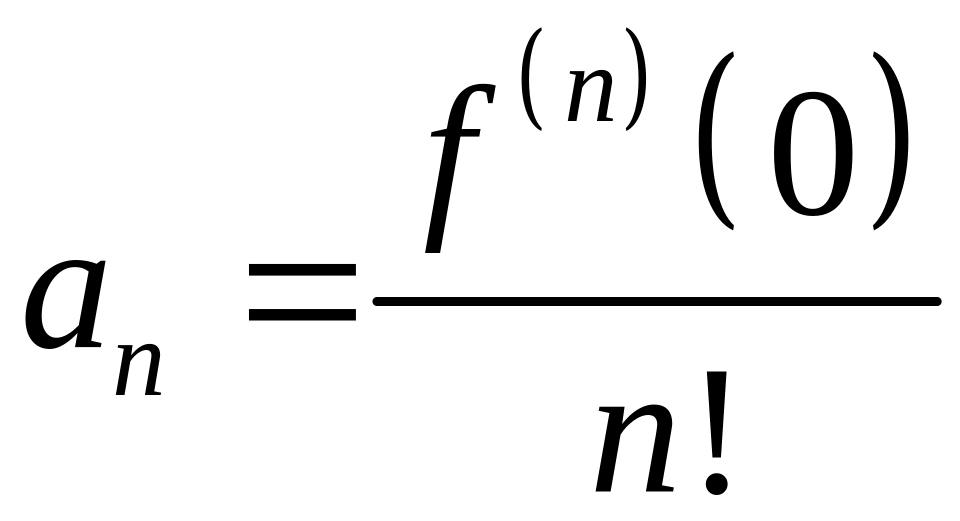- коэффициентами
Маклорена.
Говорят, что функция разложена в ряд по степеням х в окрестности точки 0.
Пример
Разложить
функцию
в ряд Тейлора в окрестности точки
.
Решение
Вычислим значения функции и ее производных в точке :
,
,
,
,
………………………………………,
,…
Составим ряд Тейлора для данной функции:
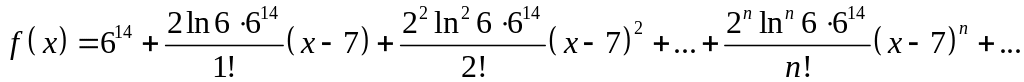или
,
.
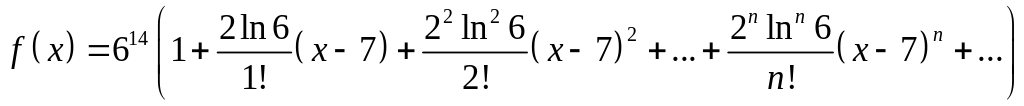Черняк Татьяна Анатольевна
Состина Елена Викторовна
Пушкина Вера Павловна
Сборник заданий по высшей математике
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
по курсУ «Математический анализ» для студентов заочного отделения