Линейно групповые коды (ЛГК)

Линейными называются коды, в которых проверочные и информационные символы связаны значениями с законами линейной комбинаторики. Т.е. с помощью определённой линейной комбинации можно построить кодовую комбинацию.

Свойства ЛГК:

1) Сумма (разность) кодовых векторов даёт вектор принадлежащий данному коду.

ЛГК относят к систематическим кодам. Минимальное кодовое расстояние равно минимальному весу ненулевых кодовых векторов. ЛГК обозначается (П, n_u) и задаются с помощью производящих матриц. Производящая матрица строится, как результат слияния информационной (И) и проверочной (П) матриц.

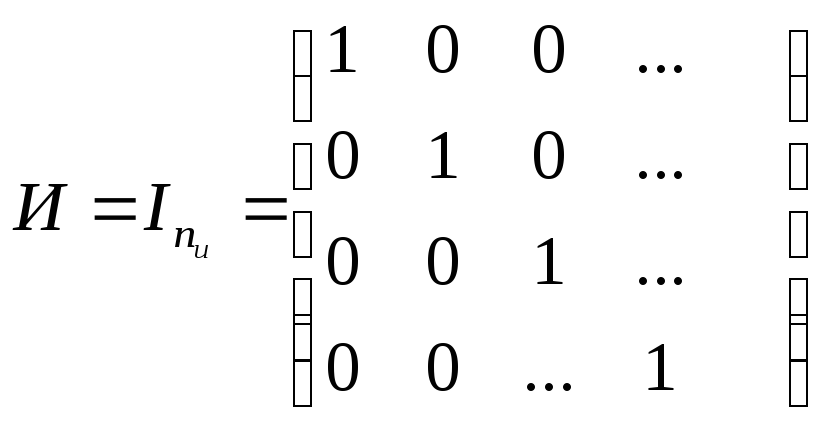Матрица имеет n_k – столбцов и n_u – строк.

В качестве П выбирают комбинации один и ноль. При этом исходят из следующих соображений: чем больше единиц в матрице П, тем оптимальней считается матрица в точке обнаружения вероятности ошибок.

Вес каждой строки матрицы П W_П = d₀ – 1. Т.о. пораждающая матрица С приводится к следующему виду:

Строки производящей матрицы представляют собой n_u комбинации искомого кода. Остальные комбинации кода можно получить двумя способами:

1. Их можно получить как результат сложения строк производящей матицы составленных в различных сочетаниях.

2. ЛГК можно построить по производящей матрице, используя информационную часть кода, путём суммирования строк матрицы П.

Пример: Построить производящую матрицу для ЛГК, способную исправлять одиночную ошибку при передачи кода на 16 сообщений.

n_u = 4; n_k = log(n_u + 1 + log(n_u + 1)) = 3

d₀ = 3; n = 7 – значность кода

(единичная матрица)

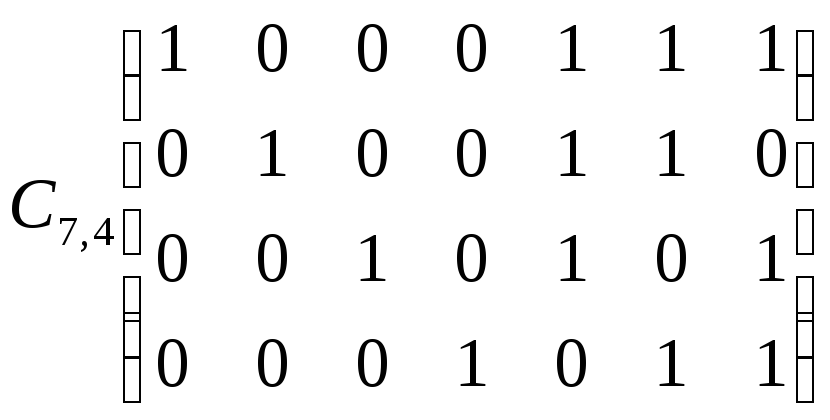
Пример: Построить образующую матрицу ЛГК, способную передавать 100 сообщений и исправлять одиночную ошибку.

N = 100 = ; n_u = 7; n_k = 4; n = 11;

Строим производящую матрицу:

Пример: Построить групповой код по заданной производящей матрице

Выписываем информационные части кода:

1) 0000 5) 0010

2) 1000 6) 1010

3. 0100 7) 0110 и т.д.

4. 1100 8) 1110

К каждой информационной части строим конкретный разряд:

1. 000

2. 111 – берём первую строку матрицы П

3. 110 – 2 – ю

4. 111 – складываем первую и вторую строку

110

001

5. 101

6. 111

101

010 - 1 - я + 3 - я

7. 110

101

011 - 2 - я + 3 - я

8. 111

110

001

100

Декодирование ЛГК

В процессе декодирования осуществляется проверки по определённой схеме. Число проверок равно числу контрольных разрядов. S(S₁, S₂, …,) – строится проверочный вектор, который называется синдром. Если вес синдрома равен нулю, то комбинация принята правильно. Если какой – либо разряд содержит единицу, то имеется ошибка. Каждому разряду соответствует свой синдром. Вид синдрома определяется с помощью производящей матрицы. Набор синдромов содержится в специальной проверочной матрице H, которая строится из матрицы H = [П^ТI_nk] I_nk - единичная матрица. Столбцы матрицы представляют значение синдрома для каждого разряда.

Схема проверок: принятый сигнал v_x представляем в виде информационной части

v_x = (a₁, a₂, …,a_n, P₁, P₂,…,P_m)

Схема проверок строится:

1. Проверка S₁

Суммируется разряд P₁ и те разряды из информационной части a₁ + …+ a_n, номера которых совпадают с номерами ненулевых разрядов первого столбца матрицы П.

2) Проверка S₂

Суммируется разряд P₂ и те разряды информационной части a₁ + …+ a_n, номера которых совпадают с номерами ненулевых разрядов второго столбца матрицы П.

Пример: Задана производящая матрица C_7,4 и составим схему проверок

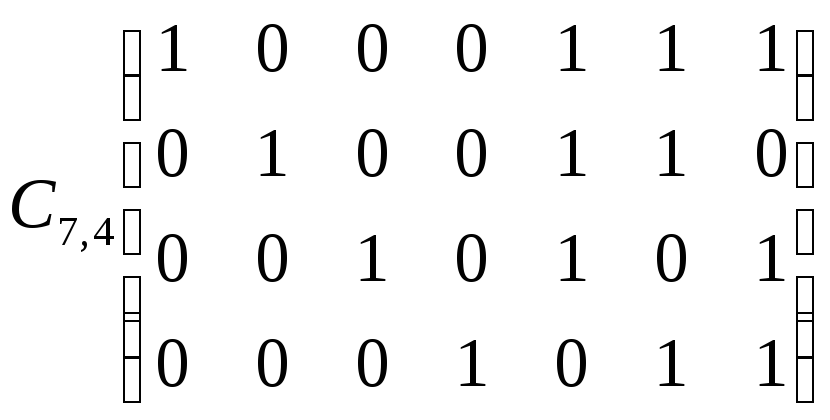
И П

S₁ = P₁ + a₂ + a₃ + a₄

S₂ = P₂ + a₁ + a₃ + a₄

S₃ = P₃ + a₁ + a₂ + a₃

Строим H:

Если разряды синдрома соответствуют одному столбцу матрицы Н, т.е. S₁ = 0, S₂ = 1, S₃ = 1, то ошибка в первом разряде.

Пример: Пусть имеется информационная часть ЛГК, которая исправляет одиночную ошибку. Дана производящая матрица С_7,4. Получим корректирующие разряды, для этого сложим первую и вторую строку, следовательно, полный код.

a₁a₂ a₃a₄P₁P₂P₃

v₁ = 1100110 v_x = 1101110

Cхема проверок осталось такой же

Проведём проверки:

S

₁ = 1 + 1 + 0 + 0 = 0

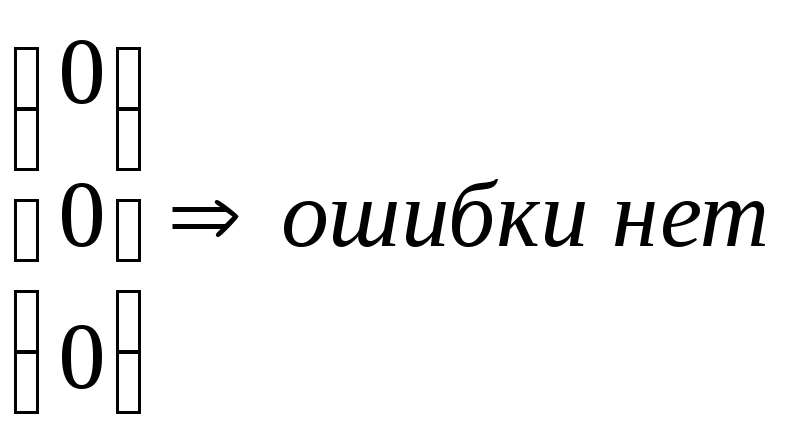
S₂ = 1 + 1 + 0 + 0 = 0

S₃ = 0 + 1 + 1 + 0 = 0

П

усть v_x = 1101110, т.е. ошибка в четвёртом разряде.

S₁ = 1 + 1 + 0 + 1 = 1

S₂ = 1 + 1 + 0 + 1 = 1 - это соответствует ошибке в четвёртому разряду

S₃ = 0 + 1 + 1 + 1 = 1