Основная теорема Шеннона о кодировании для дискретного канала без помех

1). Дискретный канал без помех:

Основная теорема Шеннона утверждает: если источник информации имеет энтропию H(z), а канал связи обладает пропускной способностью, то:

1. Сообщения, вырабатываемое источником всегда можно закодировать так, чтобы скорость их передачи v_z была сколь угодно близка к v_{z max} .

2. Не существует способа кодирования, позволяющего сделать эту скорость больше, чем v_{z max.}

Величина - называется потоком информации, т.е. согласно Шеннона, при потоке информации существует способ кодирования, при котором можно вырабатывать всю информацию, переданную источником. Если то такого способа кодирования не существует.

Теорема Шеннона (другая). Если источник информации имеет энтропию Н(z), то сообщение всегда можно закодировать так, чтобы средняя длина кода l_ср была близка к величине

Доказательство: В качестве доказательства будем использовать методику Шеннона-Фана. Предположим, что при последовательном делении совокупности кодируемых букв по методу Шеннона-Фана на меньшие группы, каждый раз удается добиться равенства вероятностей двух получаемых групп.

1. После первого деления, получается группа с вероятностью ½;

2. После второго деления, получается группа с вероятностью ¼;

и т. д. ….

После -делений получим группы с вероятностью.

Если после -делений в группе будет одна буква, то она будет иметь -значное кодовое обозначение.

При выполнении этого условия длина кодового обозначения l_i будет связана с вероятностью p_i соотношением p_i=½l_i или, преобразуя это выражение, получим l_i = log= - log p_i.

В общем случае величина log p_i целым числом не будет, поэтому в качестве _iвыбирают ближайшее большее целое число.

Величина _i будет лежать:

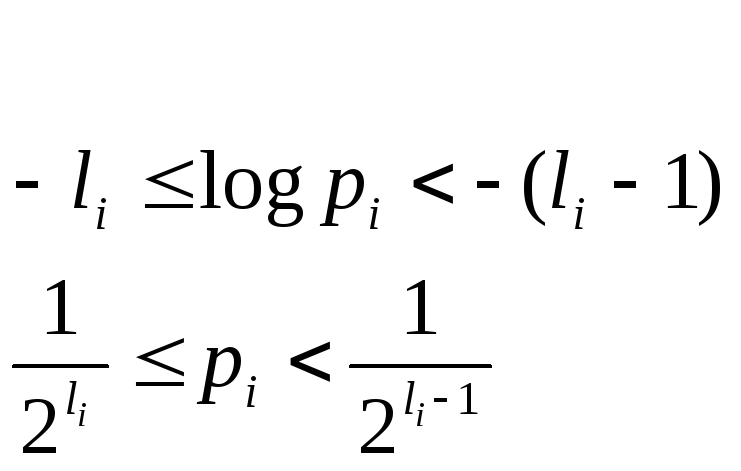
Далее Шеннон утверждал, что существует такой метод кодирования, при котором длина

_i = - log p_i

В качестве доказательства рассмотрим процедуру кодирования:

Пусть имеется алфавит с буквами и заданы вероятности их появления. Расположим буквы алфавита в порядке убывания их вероятностей.

коды

z₁ Q₁ - числа Q_i будем определять следующим образом; Q₁ = 0

z₂ Q₂ Q₂=p(z₁)

_{… …} Q₃=p(z₁) + p(z₂)

z_n Q_n …

Q_n = p(z₁) + p(z₂) + … + p(z_n-1)

Все Q_i≠0, кроме первого, следовательно, совпадения с первым не будет, все Q_i – разные и меньше единицы. Шеннон предлагает перевести каждое Q_i число в двоичную дробь.

В целом .

Эти числа можно определить из соотношения:

q_i – либо 1, либо 0.

Пример: …

Разложение каждого числа ограничивается до тех пор, пока не будет выполняться равенство:

Пример: Дан алфавит состоит из восьми букв и их вероятности. Рассмотрим процедуру кодирования

Буква	Вероятность	- log pi	li	Qi	коды
z1	1/4	2	2	0	00
z2	1/4	2	2	1/4	01
z3	1/8	3	3	2/4	100
z4	1/8	3	3	5/8	101
z5	1/8	3	3	6/8	110
z6	1/16	4	4	7/8	1110
z7	1/32	5	5	15/16	11110
z8	1/32	5	5	31/32	11111

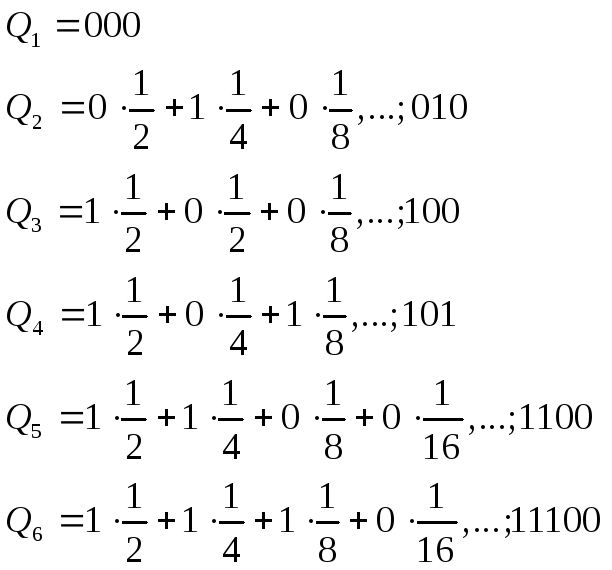
Средняя длина кодового сообщения

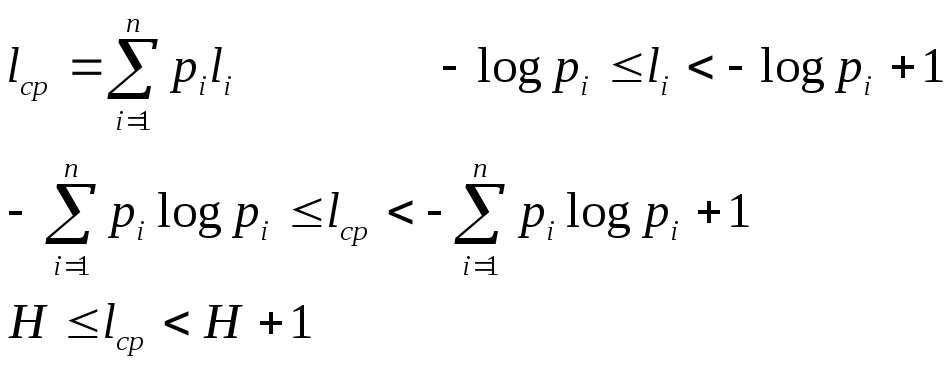
Теорема доказана

В случае кодирования буквенных блоков по N букв, получаем новый алфавит z’.

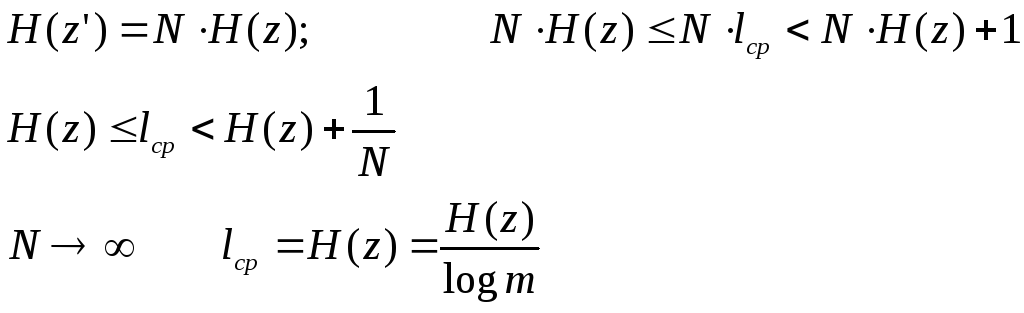
m – количество символов во вторичном алфавите, в двоичном - m = 2.

Скорость передачи Максимальная скорость

Пример: Сообщения передаются в двоичном коде. Время передачи от нуля до одной секунды, r₀ = 1 сек, секунд. Определить скорость передачи информации для случая:

1) Символы равновероятны и независимы.

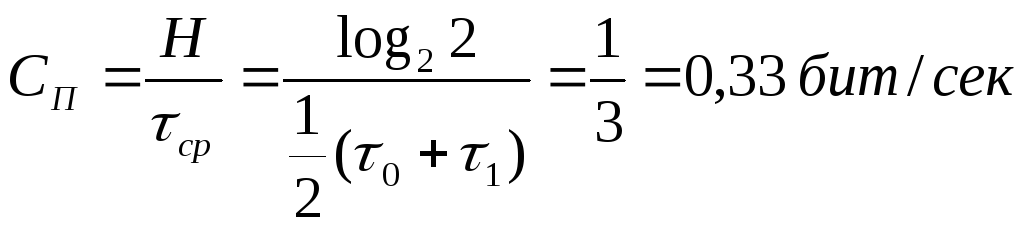
2) Символы неравновероятны