Процедура кодирования

Две буквы последнего алфавита кодируем 1 и 0. Затем кодируется предыдущий алфавит. Процесс кодирования закончен. Чтобы определить эффективность, надо посчитать среднее число символов на алфавит.

Кодирование алфавита по методу Хафмана не является однозначно определенной процедурой. Можно получать разные коды Хафмана.

Чтобы посмотреть изменение кода Хафмана, рассмотрим пример другой кодировки:

Буква а1 а2 а3 а4 а5 а6	А Вероятность 0,4 11 0,2 01 0,2 00 0,1 100 0,05 101 0,05 1010	Сжатые алфавиты
		А1 0,4 11 0,2 01 0,2 00 0,1 101 0,1 100	А2 0,4 11 0,2 10 0,2 01 0,2 00	А3 0,4 0 0,4 11 0,2 10	А4 0,6 (1) 0,4 (0)

Если посчитать , то оно не изменилось,т.е. каким образом кодировать роли не играет.

Процедура декодирования кодов Хафмана является однозначной.

Используя методику Хафмана, можно строить оптимальные коды, если для кодирования используется m элементарных сигналов. При построении таких кодов используется процедура сжатия, при которой сливаются каждый раз m букв алфавита. Последовательность сжатия приводит к алфавиту из m букв.

Число букв исходного алфавита n должно быть представляемо n = m + k *(m -1), k – целое число. Этого условия всегда можно достичь, если ввести в исходный алфавит фиктивные буквы, вероятность которых равна нулю.

Дан алфавит из 6 букв с вероятностями. Построить троичный код Хафмана 0, 1, 2.

Требуемое число букв:

n = 3 + k * (3 - 1),

k = 1 n = 5

k = 2 n = 7

не хватает одной буквы а₇ с вероятностью равной нулю

Буква а1 а2 а3 а4 а5 а6 а7	А Вероятность 0 0,4 2 0,2 10 0,2 11 0,1 120 0,05 121 0,05 122 0	С ж а т и е
		А1 0 0,4 2 0,2 10 0,2 11 0,1 12 0,1	А2 0,4 (0) 0,4 (1) 0,2 (2)

Подсчитаем энтропию

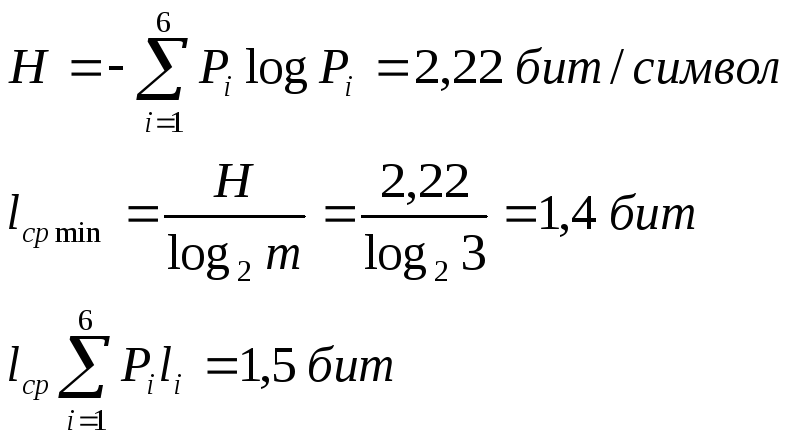m – количество символов

Существует еще одна методика

С

1

0

1

(7)

хема получения кода Хафмана с помощью кодового дерева

Д

1

0

ан алфавит. Располагаем буквы в порядке убывания вероятностей

1

0

(5)

0,5

(6)

1. а

   0,28

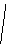
   ₁ 0,5

0

0,22

0,08

0,05

(4)

01 а₂ 0,15

011 а₃ 0,12 1

0

(2)

10 а₄ 0,1 0

0

0,13

0011 а₅ 0,04 1

0

(3)

0010 а₆ 0,04 0

0

(1)

0001 а₇ 0,03 1

00000 а₈ 0,02 0

1. Находят 2 буквы с вероятностями (а₇ и а₈) и проводят от них линию к точке, в которой вероятность равна их сумме

2. Теперь меньшими вероятностями обладают буквы а₅ и а₆. Соединяют их линиями в одной точке с вероятностью 0.08

3. Соединяем 0,08 и 0,05, получает 0,13

4. Соединяем буквы а₃ и а₄

5. Соединяем 0,15 и 0,13

И так далее…

Кодируем ветки

Обозначим цифрой один верхнюю линию узла, нижнюю ноль.

Коды представляют собой последовательность 0 и 1, которые встречаются по пути от точки с вероятностью единица, до кодируемой буквы.

Передача информации по дискретным каналам связи

Для анализа информационных возможностей канала связи используется обобщённая информационная модель каналов связи.



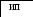
Z X Y И

ЛС

ИИ – источник информации

П₁, П₂ – преобразователи

ЛС – линия связи

ИП – источник помех

ПИ – приёмник информации

Источник информации создаёт cигналы z, которые кодируются в преобразователе П1, превращаются в сигналы x и поступают в линию связи (ЛС). В результате действия помех, сигнал Y на приёмном конце, отличается от X. Помехи создаются воображаемым источником помех (ИП) и поступают в линии связи в виде мешающего сигнала. Преобразователь П2 декодирует сигналы, и передаёт в приёмник информации. Приёмник информации перерабатывает принятое сообщение. Для организации эффективной передачи информации решают три задачи:

1. Определение максимально возможной скорости передачи информации по каналу;

2. Разработка кодов, позволяющих увеличить скорость передачи информации;

3. Согласование канала с источником.

Важнейшей характеристикой канала является пропускная способность (обозначается символом С). - Наибольшая возможная скорость передачи информации по каналу. Пропускная способность определяют следующим образом:

, где V_x- средняя скорость передачи символов, I_yx – максимальное возможное значение среднего количества информации на один символ принятого сигнала.

, - средняя длительность передаваемых символов

Взаимная информация

- характеризует потери информации.

При отсутствии помех H(x / y) = 0 и . А максимальныеI_yx = log₂m

Пропускная способность канала

m – количество символов алфавита, который кодируется