Взаимная информация

Имеется две системы: X и Y. Они взаимосвязаны. Необходимо определить, какое количество информации по системе X даст наблюдение за системой Y. Такую информацию определяют, как уменьшение энтропии системы X в результате получения сведений о системе Y.

I_yx = H(x) – H(x / y)

I_yx = I_xy = I_xy

1. Если системы X и Y независимы, то

H(x / y) = H(x) и I_yx = 0 - информации не будет

2) Система полностью зависимы

H(x / y) = H(y / x) = 0 I_yx = H(x) = H(y)

Выражения для взаимной информации можно получить через взаимную энтропию

H(x / y) = H(x, y) – H(y) I_yx = H(x) + H(y) – H(x, y)

Формула для расчёта взаимной информации

H(x) = M[ - log p(x)], H(y) = M[ - log p(y)] H(x, y) = M[ - log p(x, y)]

I_yx = M[ - log p(x) – log p(y) + log p(x, y)]

П

Сумма равна единице

Этих сведений достаточно, чтобы определить взаим-

ную информацию, создавшуюся в системе

ример: Найти полную взаимную информацию, содержащуюся в системах X и Y. Если задача на матрицы совместных вероятностей.

xi & yi	x1	x2	x3	rj
y1	0.1	0.2	0	0.3
y2	0	0.3	0	0.3
y3	0	0.2	0.2	0.4
pi	0.1	0.7	0.2

бит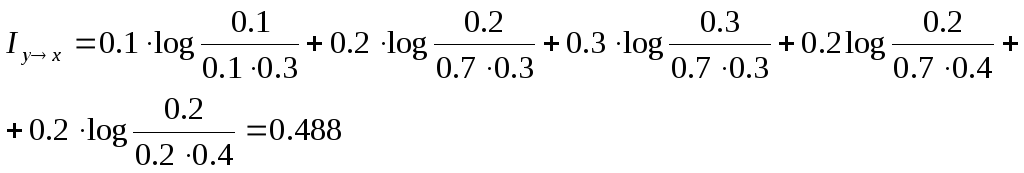

Частная информация о системе

Пусть имеется две системы X и Y и они взаимосвязаны. Определим частную информацию о системе X, содержащуюся в отдельном сообщении.

По теореме умножения вероятностей:

p_i,j = r_j * p(x_i / y_j) – подставим в

;

Частная информация как и полная, не может быть отрицательной величиной. Для вычисления частной информации через совместные вероятности используют преобразования.

, тогда

Пример: Система X и Y характеризуется таблицей вероятностей.

Определить частную информацию о системе х, содержащуюся в сообщении y1. xi & yi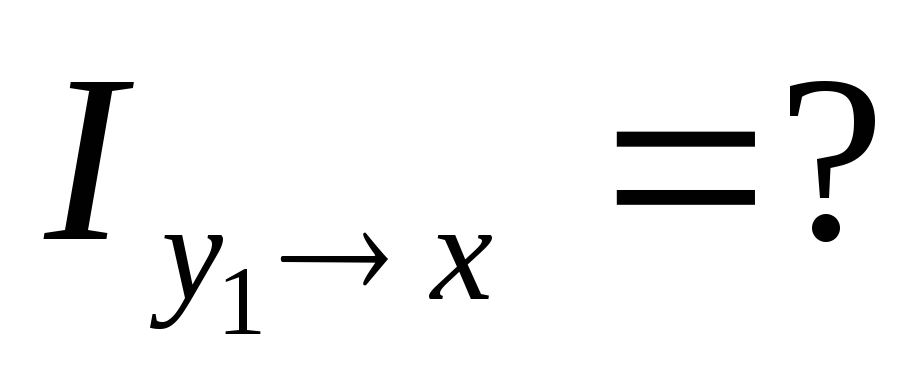	x1	x2	rj
y1	0.1	0.2	0.3
y2	0.3	0.4	0.7
pi	0.4	0.6

бит

Частная информация о событии, получаемая в результате сообщения о другом событии.

Если вероятность события p_i увеличивает вероятность, т.е. p(x_i, y_j) больше p_i, то информация больше нуля (). В противном случае, информация.

Энтропия и информация для систем с непрерывным множеством состояний

Существуют непрерывные системы. Например, время безотказной работы прибора, координаты точки попадания при выстреле.

Рассмотрим систему х, которая определяется непрерывной случайной величиной х с плотностью распределения f(x).

Определим энтропию системы. Заменим непрерывную кривую f(x) ступенчатой.

Площади прямоугольников f(x_i)*x – вероятности попадания в них случайных величин.

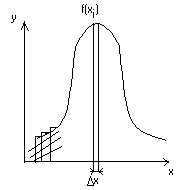
Энтропия системы:

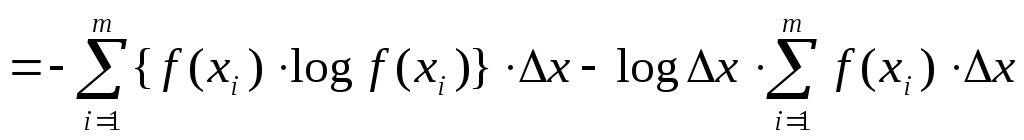
При достаточно малых сумму можно заменить интегралами

, т.к. интеграл вероятностей, следовательно

- энтропия непрерывной системы

Когда величина, особый случай. В этом случаеи , т.е. чем выше точностьопределения состояния системы, тем выше неопределённость (H(x)).

- приведённая энтропия