Определение информационных потерь в каналах связи

Производится с помощью вычисления условной энтропии. Составляется канальная матрица. Пусть по каналу связи источником информации передаются сигналы x₁, x₂, …, x_{m .} На другом конце канальной связи существует приёмник, который принимает сигнал y_1, y_2, …, y_m . В канале существуют помехи. Правильный приём - если послан сигнал x₁ и принят сигнал y₁. Если послан сигнал х_1, а принят y_j - ошибка приёма.

Влияние помех описывается с помощью канальной матрицы - таблицы.

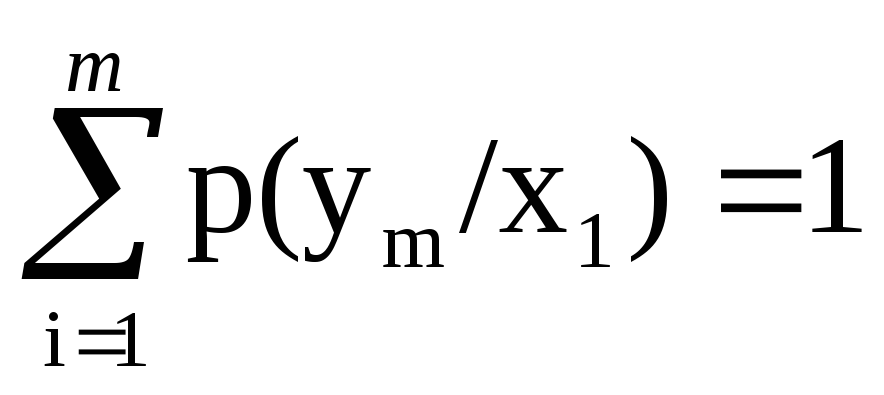
x сумма всех вероятностей условные вероятности i & yj	y1	y2	yi …	ym
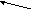x1	p(y1/x1)	p(y2/x1)	p(yj/x1)	p(ym/x1)
x2	p(y1/x2)	p(y2/x2)	p(yj/x2)	p(ym/x2)
xi …	p(y1/xi) …	p(y2/xi) …	p(yj/xi) …	p(ym/xi) …
xm	p(y1/xm)	p(y2/xm)	p(yi/xm)	p(ym/xm)

Правильный приём

Вероятности стоящие на главной диагонали выражают правильный приём, а остальные ошибочный. Если в канале нет помех, то главная диагональ состоит из единиц, а остальные нуль. Если влияние помех очень большое, то вероятности стоящие на одной строке одинаковые. Данная канальная матрица указывает влияние помех со стороны источника сообщений, они используются для исследования помех со стороны источника.

Потери информации, которые приходятся на сигнал x₁ можно подсчитать, как условную частную энтропию.

- подсчёт потерь

При передачи всех сигналов, общие потери определятся как полная условная энтропия.

их вероятности потери

Вероятности по столбцам полную группу не образуют.

Если исследуется канал со стороны приёмника, то канальная матрица имеет другой вид:

xi & yi	y1	y2	yi …	ym
x1	p(y1/x1)	p(y2/x1)	p(yi/x1)	p(ym/x1)
x2	p(y1/x2)	p(y2/x2)	p(yi/x2)	p(ym/x2)
xi …	p(y1/xi) …	p(y2/xi) …	p(yi/xi) …	p(ym/xi) …
xm	p(y1/xm)	p(y2/xm)	p(yi/xm)	p(ym/xm)

(по столбцам) образ-т правильный приём

полную группу событий

Вероятности, стоящие на главной диагонали выражают правильный приём. Вероятности, которые стоят по столбцам, образуют полную группу событий.

Пример: Влияние помех в канале связи описывается канальной матрицей. Требуется вычислить потери при передачи сигналов, если вероятность появления сигналов следующая:

p(x₁) = 0.7 p(x₂) = 0.2 p(x₃) = 0.1

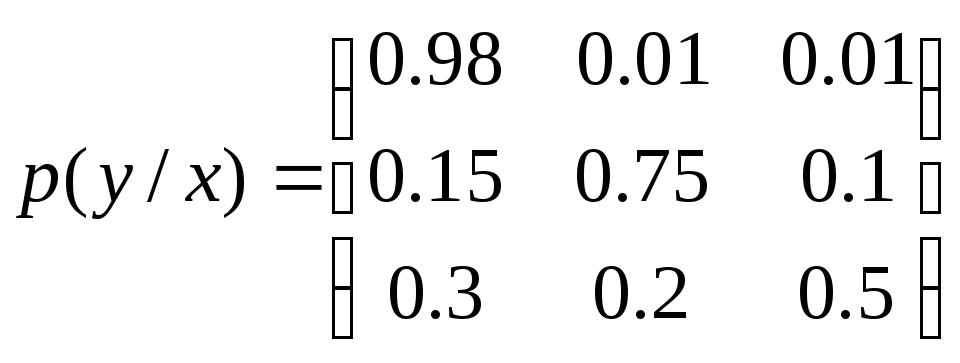
H(y / x) = -[0.7 * (0.98 log 0.98 + 2*0.01 log 0.01) + 0.2 * (0.15 log 0.15 + 0.75 log 0.75 + 0.1 log 0.1) + 0.1 * (0.3 log 0.3 + 0.2 log 0.2 + 0.5 log 0.5)] = 0.463 бит/символ .

Энтропия и информация

Пусть имеется система X с энтропией H(x). После получении информации о состоянии системы; система полностью определилась, т.е энтропия равна нулю, следовательно, информация, получаемая в результате выяснения состояния системы x равна уменьшению энтропии.

I_x = H(x) – 0 = H(x)

Количество информации приобретённое при полном выяснении состояния системы равна энтропии.

- часть информации о системе

- называют частной информацией о системе или информацией от отдельного сообщения.

Для системы с равновозможными состояниями

Полная информация

Пример: На шахматной доске в одной из клеток поставлена фигура. Вероятность нахождения фигуры на любой клетке одинакова. Определить информацию, получаемую от сообщения о нахождении фигуры в какой-либо клетке.

I_x = log 64 = 6 бит

Пример 2: Определить частную информацию от сообщения о нахождении фигуры в одной из четырёх клеток.

P = ; - вероятность сообщения= 4бит

Пример 3: Определить частную информацию, содержащаяся в сообщении случайного лица о своём дне рожденье.

- вероятность полученного сообщения; бит – количество информации

Пример 4: Определить полную информацию от сообщения о дне рождения случайного лица.

x₁ – день рожденье

x_{2 –} не день рожденье

бит

Пример 5: По цели может быть произведено n выстрелов. Вероятность поражения цели при каждом выстреле p. После k-ого выстрела (1 к  n) производятся разведка, сообщение поражена или не поражена цель. Определить к при условии, чтобы количество информации, доставляемая разведкой была максимальной.

x_k – система (цель после к-ого выстрела) имеет два состояния:

x_{1 –} цель поражена;

x₂ – промах

p₁ = 1 – (1 - p)^k p₂ = (1 - p)^k

Информация будет максимальна, когда p₁ = p_2, следовательно

1 – (1 - p)^k = (1 - p)^k , k =

p = 0.2; к = 3