Энтропия и её свойства

Рассмотрим некоторую систему, которую обозначим за X, котороя может принимать конечное множество состояний x₁, x₂, …,x_n (пример: алфавит x₁,..,x_n - буквы). Вероятность появления символов p₁, p₂, .. ,p_n.

Свойства:

1) Энтропию системы X - -всегда больше нуля. Это следует из того, что log₂ p_i – отр., p_i меньше единицы и – на - , даёт плюс.

2) Энтропия обращается в 0, когда одно из состояний достоверно, а другие невозможны, т.е. какая-то из вероятностей будет равна единице, логорифм даст ноль, следовательно, Н(x) = 0.

3) Обращается в максимальное, когда все состояния равновероятны.

4) Энтропия обладает свойством аддитивности, кода несколько систем объединяются в одну, их энтропии складываются.

Рассмотрим простейший случай. Система имеет два состояния и эти состояния равновероятны.

H(x) = - (0.5 log 0.5 + 0.5 log 0.5) = 1 бит/символ xi	x1	x2
p1	0.5	0.5

Определить энтропию системы X, которая имеет n равновероятных состояний

- log 1 + log n = log n xi	x1	x2 …	xn
pi		…

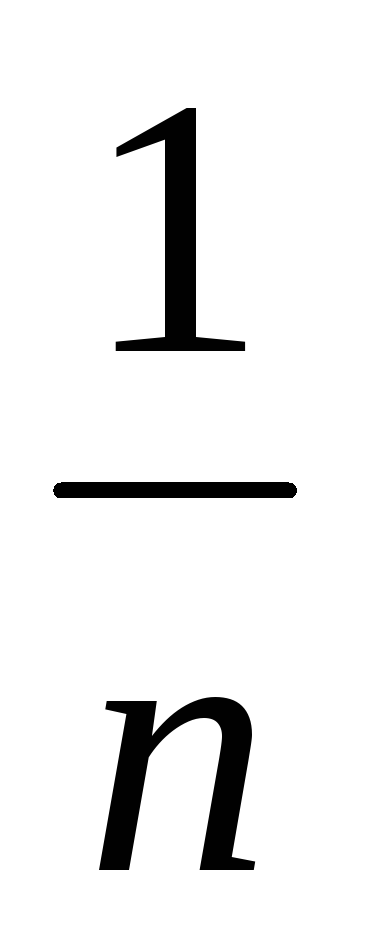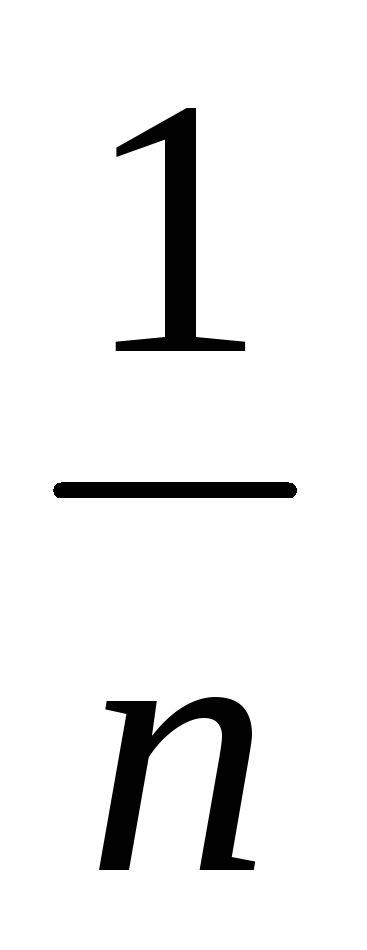
- это частный случай, когда все вероятности одинаковы.

Пример: Система X имеет восемь состояний. Определить энтропию. (состояния равновероятны)

n = 8

Пример: Определить H, состояние которой описывается таблицей.

Система имеющая пять состояний

бит/символ xi	x1	x2	x3	x4	x5
p1	0.01	0.01	0.01	0.01	0.96

Иногда энтропию определяют через математическое ожидание

H(x) = M[-log₂ p(x)] – это позволяет упростить математические выкладки.

Пример: Алфавит состоит из букв a, b, c, d. Даны вероятности p_a = p_b = 0,25; р_с = 0,34; p_d = 0.16

H(x) = - (2*0.25 log 0.25 + 0.34 log 0.34 + 0.16 log 0.16) = 1.952 бит/символ

Энтропия сложной системы

Под объединением двух систем X и Y с возможными состояниями x₁,x₂,…,x_n , y_1, y_2,…,y_{m ,} понимается сложная система (x, y), состояние которых x_i,y_i; представляют собой все возможные комбинации состояний x_i,y_i .

Число возможных состояний равно m х n.

Обозначим символом p_i,j , вероятность того, что система может находиться в состоянии p(x_i,y_i). Тогда вероятность p_ij можно представить в виде таблицы совместных вероятностей.

таблица совместных вероятностей xi & yi	x1	x2	…	xn
y1	p11	p21	…	pn1
y2	p12	p22		pn2
…	…	…	…	…
ym	p1m	p2m	…	pnm

; ; H(x, y) = M[- log p(x, y)].

Пусть системы X, Y независимы. Тогда по теореме умножения вероятностей имеем:

p(x, y) = p(x) * p(y)

Прологарифмируем левую и правую часть

log p(x, y) = log p(x) + log p(y)

H(x, y) = M[- log p(x) – log p(y)]

H(x, y) = H(x) + H(y), если независимые системы, то их энтропии складываются.

Условная энтропия. Объединение зависимых систем.

Пусть имеем две зависимые системы X и Y. Пусть система X приняла состояние x_i, а система Y приняла состояние y_i , тогда обозначим p(y_{i /} x_i) – это условная вероятность того, что система Y примет состояние y_i, при условии, что система X приняла состояние x_i.

Неопределённость системы в состоянии Y определяется частной условной энтропией.

- система X находится в конкретном состоянии

; - условное математическое ожидание