Дискретный канал с помехами

Характеризуется канальной матрицей

…

Взаимная информация

Энтропия на выходе приёмника

Средняя условная энтропия

- это максимальное значение определить сложно.

…

…

Определим пропускную способность канала связи, по которому передаются двоичные сигналы со скоростью v_x, если вероятность искажения сигнала равна p.

Имеет источник информации, приёмник информации.

Разложение выполним в виде диаграммы

Правильный приём

Канал такого типа называют симметричным бинарным, (т.к. два числа)

Искажение

Определим среднюю условную энтропию

Учитывая, что

, получим, что

 объединили

- , т.е потери не будут зависеть от характерис-тики источника

Поэтому

Пропускная способность канала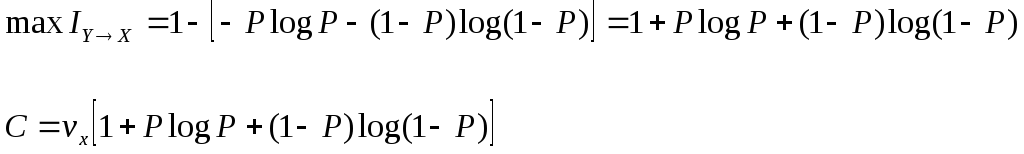

Рассмотрим два крайних условия:

1. Вероятность искажения (Р=0), следовательно, помех нет, следовательно, С = v_x и она имеет свое максимальное значение

2. Р=1/2. Значение С = 0 – это минимальное значение пропускной способности

Пример: Определить пропускную способность канала связи, способного передавать 100 симв./сек . Каждый символ искажается с вероятностью 0,01.

Теорема о кодировании Шеннона для дискретного канала с помехами

Если источник информации имеет энтропию H(z), а канал обладает пропускной способностью С, то:

1. Сообщение, вырабатываемое источником, всегда можно закодировать так, чтобы скорость передачи v_z была близка величине v_{z max.}

И чтобы при этом вероятность ошибки в определении переданного символа была меньше заданного числа.

2. Не существует метода кодирования, позволяющего вести передачу со скоростью выше

v_{z max} и с малой вероятностью ошибки.

То есть, если H’(z) ≤ C, то может быть подобран специальный код, позволяющий вести передачу с малой вероятностью ошибки. Если H’(z) > C то такого кода не существует.

Очевидно, что при уменьшении скорости передачи, можно повысить достоверность, например, методом многократного повторения. Для обеспечения нулевой ошибки, кажется, что скорость передачи должна стремиться к нулю. Теорема же утверждает, что всегда можно обеспечить скорость передачи равной V_{z max} путем выбора подходящего ввода.

Корректирующие коды

Это коды, которые позволяют обнаруживать и исправлять ошибки.

n – значность кода (из скольки символов состоит данная кодовая комбинация)

N₀ = 2ⁿ, n – число возможных кодовых комбинаций.

Идея возможности обнаружения ошибок заключается в том, что для передачи используются не все комбинации, а только их часть N.

И это значение N<N₀.

Используемые комбинации N называются разрешенные, а остальные N₀–N – это запрещенные комбинации.

Если в результате действия помех разрешенная комбинация превращается в запрещенную, то это обнаруживает наличие ошибки. Если совокупность ошибок превращает одну разрешенную комбинацию в другую разрешенную комбинацию, то такие ошибки обнаружены не будут.

Примером кода, обнаружившего одиночную ошибку, является коды с контролем по четности. Сущность таких кодов состоит в следующем:

К исходной кодовой комбинации добавляют 1 или 0, таким образом, чтобы количество (сумма) единиц всегда была четной. Сбой любого одного символа обнаружит ошибку.

информационный

контрольный Код 1 00 01 10 11

Код 2 00 01 10 11

0 1 1 0

Чтобы принять сигнал правильно, надо повторить передачу.

Количество символов, на которое одна кодовая комбинация отличающаяся от другой кодовой комбинации, называется кодовым расстоянием и обозначается буквой d. d₀ – минимальное кодовое расстояние – минимальное количество символов, на которое кодовая комбинация отличается друг от друга.

Для того, чтобы определить кодовое расстояние достаточно просуммировать кодовые комбинации по правилам двоичного поля и подсчитать число единиц в полученном результате.

Пример: Для кода 1

А₁ = 00 0  0 = 0 Правила:

А₂ = 01 1  0 = 1 четн. – 0

А₃ = 10 0  1 = 1 нечетн. – 1

А₄ = 11 1  1 = 0

Определим кодовую комбинацию

А₁А₂  d = 1 А₃А₄  d = 1

01 01

Для кода 2

А₁=000 А₂А₄ 011 А₃А₂ 101

А₂=011 110 d = 2 011 d = 2

А₃=101 101 110

А₄=110

Ошибку можно не только обнаружить, но и исправить, если принятая кодовая комбинация ближе к исходной, чем к любой другой разрешённой комбинации.

Пример: Построим код: К коду 2 добавим два символа, повторив первых два символа получим код 3:

Код 2

А₁=000

А₂=011

А₃=101

А₄=110

Код 3

00 01 10 11

000 101 110 011

информационные разряды контрольные разряды

Определим кодовое расстояние между комбинациями

Строим матрицу кодовых расстояний

	А1	А2	А3	А4	d0 = 3
А1	0	3	3	4
А2		0	4	3
А3			0	3
А4				0

Пусть передаётся комбинация А₃, и она содержит ошибку

матрица кодовых расстояний

	А1	А2	А3	А4
Vx	4	3	1	2

v_x ближе всего к А₃, следовательно посылалась А₃ и мы ошибку исправили.

Корректирующая способность кода зависит от минимального кодового расстояния d₀. Если

d₀ = 3, то он может исправлять ошибку, то есть корректирующую способность кода можно повышать, если увеличивать минимальное кодовое расстояние.

Для построения кодов, которые обнаруживают и исправляют одиночную ошибку d₀ = 3, должно выполняться неравенство:

, где

n_и – количество информационных разрядов

n – значность кода

n_к – количество контрольных разрядов

n = n_и + n_к

Поэтому результаты сведем в таблицу:

n	5	6	7	8	9	10	11	12	13	14	15
nи	2	3	4	4	5	6	7	8	9	10	11
nк	3	3	3	4	4	4	4	4	4	4	4

Предположим, что строим код на тридцать два сообщения n_и = 5, выделяем столбец

n_к = 4

n = 9

Расчеты можно вести по формуле.

Для кода, который обнаруживает двойную ошибку, а исправляет одиночную:

- значения округляются в большую сторону

- до большего целого числа

Обозначим буквой:

r – кратность обнаруживающих ошибок;

s – кратность исправляемых ошибок;

Тогда для кодов обнаруживающих и исправляющих ошибки:

d₀ = r + s + 1,

для кодов, которые только обнаруживают ошибки d₀ = n + 1,

для кодов, которые только исправляют ошибки d₀ = 2s + 1 (когда r > s).

Если

d₀ r s

10 0 отличие комбинации

21 0 обнаружение одиночной ошибки

31 1 обнаружение одиночной ошибки и исправление одиночной ошибки

32 0 обнаруживающий 2-ую ошибку

Количество контрольных разрядов и значность кода для разных минимальных кодовых расстояний, связано соотношением:

Для кодов, обнаруживающих все трехкратные ошибки.

количество обнаруженных ошибок

Для кодов, исправляющих двойные ошибки

Для кодов, исправляющих тройные ошибки:

Для кодов, исправляющих S ошибок:

Пример: Требуется передавать, обнаруживающим трёхкратные ошибки, все комбинации пятизначного двоичного кода. Чему равна общая длина кода ?

r – кратность обнаруживающих ошибок.

s – кратность исправляемых ошибок.

n_и = 5; n_к = 1 + log[6 + log6] = 5

n = n_и + n_к = 10

Пример: Определить количество информационных разрядов кода длиной в пятнадцать символов, если код исправляет две ошибки.

n=15

n_и = n - n_к = 15 – 7 = 8