3.2. Интервальная оценка характеристик случайных величин. Доверительные границы

Точечные оценки, рассмотренные в предыдущем пункте, дают приближенное значение истинной случайной величины, сама же выборочная характеристика U является случайной величиной.

С некоторой вероятностью (уровень значимости) случайные значения величиныU попадут в некоторый интервал вокруг истинного значения (рис. 3.1 а) :

. (3.7)

Правомерна и обратная постановка задачи: определить интервал около вычисленной характеристики U, который накроет истинное значение (рис. 3.1 б):

. (3.8)

Рис. 3.1

Оценка, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр, называется интервальной оценкой.

Интервал от доимеет случайные концы и носит названиедоверительного интервала, а вероятностьназывается доверительной вероятностью (или уровнем доверия).

Один конец интервала, определенный соотношением , называется нижней доверительной, другой конец -- называется верхней доверительной границей. Доверительные границы определяют интервал, в котором с достаточно высокой вероятностьюнаходится значение.

Если , то величинабудет находиться в интервале отдо бесконечности с вероятностью:

. (3.9)

Если , т.е.=0 , то величинабудет не больше, или, другими словами, находится в интервале от 0 дос вероятностью:

. (3.10)

Выражения (3.9) и (3.10) определяют односторонние доверительные границы для характеристики . Односторонние доверительные границы применяются в тех случаях, когда надо убедиться, что одна случайная величина строгобольше другой (или строго меньше другой).

Двусторонняя доверительная вероятность есть вероятность нахождения истинного значениямежду нижней и верхней доверительной границами:

. (3.11)

Двусторонние доверительные границы применяются в тех случаях, когда при сравнении двух случайных величин представляют одинаковый интерес как положительные, так и отрицательные разницы между изучаемыми величинами.

Имеет место соотношение:

. (3.12)

В частном случае, когда , уравнение (3.12) записывается в виде:

. (3.13)

Величина (ширина) доверительного интервала характеризует точность выборочной оценки исследуемой характеристики, а именно, чем меньше эта величина, тем точнее выборочная оценка. Доверительная вероятность характеризует достоверность полученной интервальной оценки.

3.3. Определение доверительных границ для различных законов распределения

Доверительные границы определяются в зависимости от вида закона распределения исследуемой случайной величины.

Для случая нормального распределения доверительные границы определяются по критерию Стьюдента. В соответствии с распределением Стьюдента отклонение выборочной средней от математического ожиданияпри наличии выборки объемаn равно:

. (3.14)

Для нижней доверительной границы математического ожидания на основании формулы (3.8) получаем:

. (3.15)

Соответственно для верхней доверительной границы имеем:

, (3.16)

где - выборочное среднеквадратическое отклонение (3.4). В формулах (3.15) и (3.16)- коэффициенты Стьюдента, помещенные в табл. П.8. Вход в таблицу производится по значению двухсторонней вероятностии величине степени свободыk=n-1. Например, имеется статистический материал с

n=25 и принято =0,95. По таблице дляк=24 и заданного определяем=2,064. По выборке определяемпо формуле (3.1), несмещенную дисперсию по формуле (3.3) и среднеквадратическое отклонениепо формуле (3.4). Окончательно по формулам (3.15) и (3.16) определяем нижнюю и верхнюю доверительные границы. Иногда в случае нормального распределения необходимо знать не только доверительные границы математического ожидания, но и доверительные границы среднеквадратического отклонения. Нижняя и верхняя границы значения среднеквадратического отклонения соответственно равны:

; (3.17)

. (3.18)

Коэффициенты иопределяются по табл. П.9, вход в которую производится по величине доверительной вероятностии числу степеней свободыk=n-1 Для экспоненциального распределения с параметром распределения , который равен обратной величине математического ожидания, его опытное значение равно:

, (3.19)

где - значение случайной величины в выборке объемомn . Доверительные границы параметра λ находятся по формулам:

; (3.20)

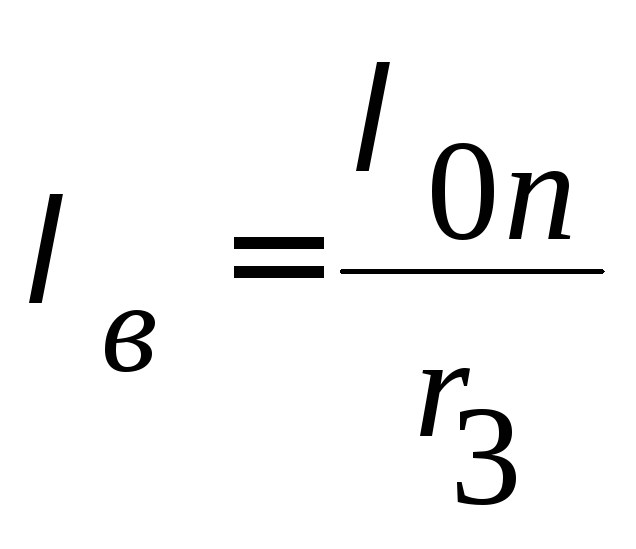, (3.21)

где значения величин иопределяются по табл. П.10 а и П.10 б, вход в которые производится по доверительной вероятностии числуm, означающему, например, число испытаний, при каждом из которых произошел отказ, или число отказов при заданном числе испытаний. Во втором случае определяется вероятность отказа и ее доверительные границы.

Так, если при n одинаковых опытах с невосстанавливаемыми изделиями получено m отказов, то нижняя и верхняя границы вероятности отказов будут равны:

; (3.22)

, (3.23)

где r₁ и r₂ определяются по табл. П.10 а и П.10 б.

Если случайная величина x имеет распределение Вейбулла с параметрами a и b, то, как это было показано в п. 1.23, закон распределения имеет вид:

.

Сравнивая эту формулу с формулой для экспоненциального распределения (1.9), можно заметить, что случайная величинаимеет экспоненциальное распределение с параметром.

Зная из эксперимента значения, можно определитьпо формуле (3.1) ипо формуле (3.4). По величине коэффициента вариациииз табл. П.4 определяем величиныв и .

По значению параметра в определяем значения :

.

По аналогии с формулой (3.19) для экспоненциального распределения среднее значение равно :

, (3.24)

откуда . (3.25)

Так как для распределения Вейбулла , то

. (3.26)

Учитывая, что и учитывая выражения (3.20) и (3.21) для нижней и верхней доверительных границ для, получаем:

; (3.27)

, (3.28)

где икак и для экспоненциального распределения определяются по табл. П.10 а и П.10 б.

Если случайная величина t имеет гамма-распределение, то для плотности вероятностей в форме (1.20) параметрами этого распределения являются иm, причем m известно, а определяется из опыта.

Выборочная средняя равна

. (3.29)

Среднеквадратическое отклонение величины равно:

. (3.30)

Распределение величины приближенно нормальное, поэтому для доверительных границ можно записать выражения:

; (3.31)

, (3.32)

где - квантили нормального распределения, определяемые по табл. П.3.

Для неизвестного параметра справедливы соотношения:

; (3.33)

; (3.34)

, (3.35)

где величина определяется по табл. П.3.

Для случая логарифмически-нормального распределения (1.2.5) приближенно можно записать и, тогда формула для логарифма математического ожидания исходной случайной величиныy имеет вид:

. (3.36)

Приближенно можно считать, что распределен нормально, тогда для доверительных границ можно записать:

; (3.37)

, (3.38)

где величина определяется по табл. П.3.