8.2. Дифференциальные уравнения Колмогорова. Предельные вероятности состояний

Для случайных Марковских процессов с дискретными состояниями и непрерывным временем в графе состояний у стрелок переходов из состояния в состояние указываются плотности вероятности переходов . Потоки событий, переводящие систему из одного состояния в другое, являются пуассоновскими.

Пусть система имеет конечное число дискретных состояний . Схема случайного процесса представляет собой ступенчатую кривую (рис. 8.2), причем на рис. 8.2 изображен один из возможных вариантов, одна из возможных реализаций процесса.

Рис. 8.2.

Смена состояний в процессе происходит в некоторые случайные моменты времени, распределение которых подчиняется экспоненциальному закону.

Для любого момента времени вероятность обозначенных выше состояний есть, при этом соблюдается условие нормировки.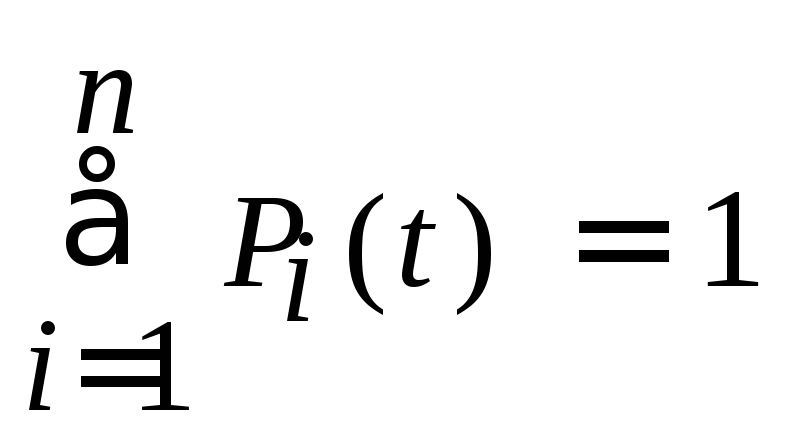

Чтобы найти все вероятности состояний , необходимо решить систему дифференциальных уравнений Колмогорова.

. (8.3)

Здесь сумма первых чисел означает сумму потоков вероятностей, идущих в данное состояние, а второй – сумму потоков вероятностей, идущих из данного состояния.

Если предельные вероятности состояний системы существуют, то имеет место установившийся режим, для которого производные будут равны нулю. В этом случае система дифференциальных уравнений Колмогорова превращается в систему алгебраических уравнений. Совместно с нормированным условием эти уравнения дают возможность вычислить все предельные вероятности состояний.

8.3. Решение системы алгебраических уравнений предельных вероятностей состояний с помощью математического пакета Mathcad

Пусть имеется исходная система n линейных алгебраических уравнений относительно n неизвестных: .

Матрица:

называется матрицей системы.

Матрица

называется матрицей правых частей системы.

Решение системы алгебраическихуравнений может быть получено методом Крамера, с помощью обратной матрицы или с помощью встроенной функции find.

Для конкретности рассмотрим систему уравнений, составленную по графу состояний, изображенному на рис. 8.3.

Система алгебраических уравнений

для этого графа состояний будет иметь

а21 а12 а13 следующий вид :

-(a12 + a13 )P1 + a21P3 = 0

а32 a12P1 – a21P2 + a12P3 = 0

Рис.8.3 a13P1 – a32P3 = 0

Если добавить к этой системе нормировочное условие Р1 + Р2 + Р3 = 1 ,

то одно из уравнений системы можно исключить (целесообразно исключить самое громоздкое) и решать систему одним из указанных выше методов.

Пусть, например, исключено второе уравнение. Имеем следующую исходную систему уравнений:

- (а12 + а13)Р1 + а21Р3 = 0

а13Р1 – а32Р3 = 0 (8.4)

Р1 + Р2 + Р3 = 1

Решение системы уравнений методом Крамера

Обозначим матрицу коэффициентов левых частей исходной си стемы уравнений символом А, а матрицу правых частей символом В.

Далее записывается следующий текст:

ORIGIN := 1

А:=B:=

Далее определяется значение детерминанта .

Заменяя последовательно столбцы матрицы А значениями величин строк матрицы В, определяем значения детерминантов D1, D2, D3:

D1=… D2=…

D3=…

Значения неизвестных P1, P2 и P3 определяются по формулам:

Решение системы алгебраических уравнений с помощью обратной матрицы

Обратная матрица формируется с помощью панели Matrix путем вызова операции