
Подгон Экзамена Дискретная Математика(НЕ ПОЛНЫЙ)
.docxВопросы идут по порядку тем
источник: http://emirs.miet.ru/oroks-miet/upload/ftp/pub/2012_1/4fb547801c647/lect3_m1_vm1_vm1_DM_231300.62.pdf + тексты лекций
Булев вектор


Функции алгебры логики
![]()
Задание булевых функций таблицей истинности и вектором значений.


Элементарные булевы функции одной и двух переменных.


Формулы над множеством функций

задание функций формулами (пункт 5)

Доказательство равносильности формул с использованием таблиц истинности.

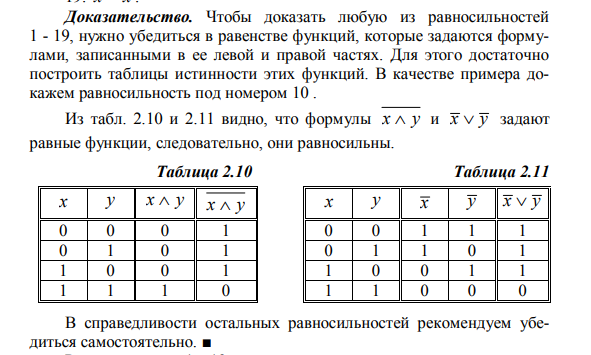
Основные равносильности над множеством {∨,∧,¬,0,1}.
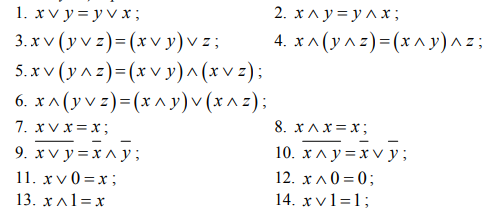

Упрощение формул методом равносильных преобразований. (пример)

Фиктивные и существенные переменные,

равные функции,

алгоритм удаления и введения фиктивных переменных


Двойственная функция.

Принцип двойственности.


Разложение булевой функции по переменным

Совершенная дизъюнктивная нормальная форма (СДНФ).

соверщенная конъюнктивная нормальная форма (СКНФ).

Представление булевой функции в виде СДНФ и СКНФ


Полином Жегалкина,

![]() степени
степени
представление булевой функции полиномом Жегалкина.

Элементарная конъюнкция,

ранг элементарной конъюнкции.

Дизъюнктивная нормальная форма (ДНФ),

сложность ДНФ

Минимальная ДНФ.


Импликанта, простая импликанта.

Сокращенная ДНФ.

Тупиковая ДНФ.

представление функции в виде минимальной, тупиковой, сокращенной ДНФ (без примеров)




Функции, сохраняющие 0 и 1

Самодвойственные функции.

Монотонные функции.


Линейные функции.

Классы Поста.




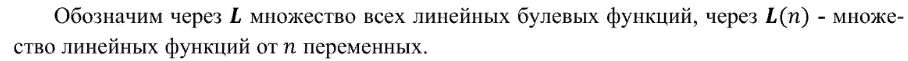
Замыкание системы булевых функций.




Понятие полной системы.

Теорема о полноте двух систем.

Лемма о функции, сохраняющей 0

Лемма о функции, сохраняющей 1

Лемма о несамодвойственной функции.

Лемма о монотонной функции.
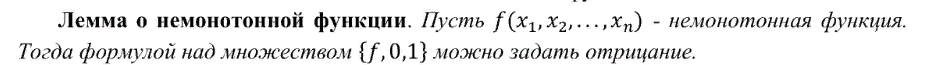
Критерий полноты системы булевых функций (теорема Поста).

Базисы.

Граф, его вершины и ребра.

Смежные вершины и кратные ребра, и петли

Инцидентные вершины и ребра.


Степени вершин. Висячие и изолированные вершины.

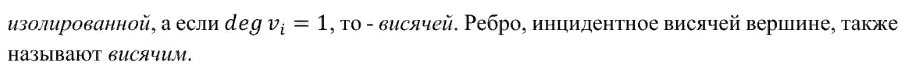
Лемма о рукопожатиях. Диаграмма графа.

Изоморфные графы.


Специальные виды графов: обыкновенные, полные, двудольные, полные двудольные графы.

Матрица смежности и матрица инцидентности.


Подграф.

Операции над графами: объединение, пересечение, декартово произведение.
Пути, цепи, циклы на графе.
Отношение достижимости (связности), компоненты связности графа.
Мосты графа, связь между мостами и циклами.
Цикломатическое число графа
Линейное пространство циклов.
Алгоритм построения фундаментальной системы циклов
Дерево, лес, их характеристические свойства.
Остовы графа.
Число остовов в графе с занумерованными вершинами.
Алгоритм Краскала отыскания минимального остова.
Кодирование деревьев.
Укладка графов в трехмерном пространстве.
Укладка графа на плоскости.
Планарные графы.
Связь между числом вершин, ребер и граней плоского графа.
Гомеоморфные графы.
Критерии планарности.
Алгоритм укладки графа на плоскости.
Эйлеровы цикл и цепь, критерии их существования.
Алгоритм построения эйлерова цикла.
Гамильтоновы цикл и цепь.
Задача коммивояжера.
раскраска графа
хроматическое число
Критерий бихроматичности.
Раскраска плоских графов.
Ориентированный граф (орграф)
диаграмма орграфа
Изоморфные орграфы.
Матрицы смежности инцидентности орграфа.
Ориентированные пути, цепи, циклы.
Слабая и сильная связность.
Орграф и его элементы.
Изоморфные орграфы.
Матрицы смежности и инцидентности орграфа.
Пути, цепи, циклы на орграфе.
Слабая и сильная связность орграфа.
Понятие ориентированного дерева.
Графы и бинарные отношения.
Постановка задачи об отыскании кратчайших путей в сети. Алгоритм Дейкстры, его обоснование.
Сеть. Поток в сети.
Величина потока.
Максимальный поток.
Дополняющая цепь.
Разрез в сети.
Минимальный разрез.
Алгоритм Форда – Фалкерсона.
Обоснование алгеритма (Леммы 1,2,3 и теорема Форда-Фалкерсона).
Алгоритм поиска в ширину на ориентированных графах.
Паросочетания: наибольшее, максимальное, совершенное.
Задача о поиске наибольшего парососчетания в двудольном графе: постановка и алгоритм
решения задачи.
Задача о поиске совершенного паросочетания минимального веса (задача
о назначениях): постановка и алгоритм решения задачи.
Схема из функциональных элементов.
Входы, функциональные элементы, выходы схемы.
Сложность схемы.
Глубина вершины.
Функции, реализуемые в вершинах схемы.
Функции, реализуемые схемой.
Проблема анализа и проблема синтеза схем.
Упорядоченная бинарная диаграмма решений (УБДР).
Сток, внутренняя вершина.
Сложность УБДР. Минимальная УБДР.
Сокращенная УБДР.
Правило сокращения. Правило слияния.
Построение сокращенной УБДР для функции, заданной таблицей и формулой.
