5.5. Частные решения уравнения диффузии

Из общих решений уравнения диффузии при D = const, приведённых в 5.3, могут быть получены частные решения для различных начальных и граничных условий.

1. Диффузия с постоянной поверхностной концентрацией (из неогра-ниченного источника). При постоянной концентрации на поверхностности в течение всего процесса диффузии (С(0, t) = C_s = const) и первоначальном отсутствии примеси в образце (C(x, 0) = 0) профиль распределения примеси выражается дополнительной функцией ошибок (рис. 5.4)

.

Количество примеси, продиффундировавшее в образец,

.

Описанные условия соответствуют первой стадии диффузии.

2. Диффузия из слоя конечной толщины. Исходная примесь первоначально находится в слое толщиной h, т. е. C(x, 0) = C₀ при x ≤ h и

C(x, 0) = 0 при x > h, испарение с поверхности отсутствует (отражающая граница), . В этом случае решение уравнения диффузии имеет вид (рис. 5.5)

3. Диффузия из бесконечно тонкого слоя (из ограниченного источника).

Для бесконечно тонкого слоя при h → 0 из последнего выражения с учётом соотношения получаем

где Q – количество примеси в слое, Q = C₀h.

4. Двухстадийная диффузия. Если эффективная толщина диффузион-ного слоя, сформированного на первой стадии h₁ = , значительно меньше толщины диффузионного слоя, сформированного на второй стадии h₂ = , или D₁t₁ << D₂t₂, тогда можно использовать выражение, полученное ранее для бесконечно тонкого слоя,

,

где Q – количество примеси в слое, введённое во время первой стадии,

.

Здесь индекс 1 указывает на первую стадию, а индекс 2 – на вторую.

5. Многоэтапная диффузия. Под многоэтапной диффузией понимается диффузия в несколько этапов, на которых граничные условия не изменяются. В этом случае вид выражений для распределения примеси не изменяется, а произведение Dt заменяется на , где i – номер этапа; t_i – длительность i-го этапа. Например, при двухэтапной диффузии из постоянного источника, когда концентрация на поверхности не меняется, С₁(0, t) = С₂(0, t) = C_s = = const,

.

При двухэтапной диффузии из ограниченного источника, когда граница при x = 0 непроницаема и количество примеси в слое не меняется, Q₁ = Q₂ = Q = const,

.

5.6. Концентрационная зависимость коэффициента диффузии

При высоких концентрациях примеси (C > n_i, где n_i – собственная концентрация носителей заряда при температуре диффузии) коэффициент диффузии легирующей примеси в полупроводниках перестаёт быть постоянным и начинает зависеть от концентрации примеси. Соответственно изменяется и вид профиля (рис. 5.6). При диффузии из постоянного источника с поверхностной концентрацией C_s < n_i, распределение примеси (кривая 1) описывается дополнительной функцией ошибок (пунктир 1 на рис. 5.6). Тогда как при поверхностной концентрации C_s > n_i распределение примеси (кривая 2) отличается от дополнительной функции ошибок (кривая 2) и имеет “плато” вблизи поверхности, где коэффициент диффузии максимален.

Причиной концентрационной зави-симости коэффициента диффузии легирующих примесей является присутствие в полупроводнике заряженных собственных точечных дефектов и влияние на их концентрацию уровня Ферми. Установлено, что СТД в кремнии могут быть не только нейтральными, но и иметь заряды ±1 и ±2.

Связь между концентрациями заряженных и нейтральных СТД выражается соотношениями Шокли–Ласта. Так, например, для однократно отрицательно заряженных вакансий V^– они имеют вид

,

где E_F – уровень Ферми; и – уровень отрицательно заряженной вакансии и фактор его вырождения, E_c – положение дна зоны проводимости, N_c – эффективная плотность состояний в зоне проводимости, n – концентрация электронов. Для двукратно заряженных вакансий V^2–

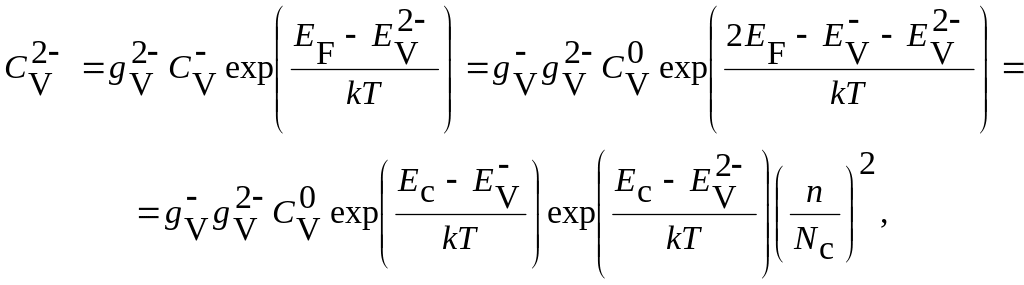
где и – уровень дважды отрицательно заряженной вакансии и фактор его вырождения. Для однократно и двукратно положительно заряженных вакансий V⁺

,

где , , и – уровни однократно и двукратно заряженных вакансий и факторы их вырождения соответственно; E_v – положение потолка валентной зоны проводимости; N_v – эффективная плотность состояний в валентной зоне; p – концентрация дырок. Аналогичные соотношения можно записать и для концентраций заряженных собственных междоузельных атомов.

Таким образом, концентрации отрицательно заряженных СТД пропорциональны концентрации электронов n, двукратно отрицательно заряженных СТД пропорциональны n², концентрации положительно заряженных СТД пропорциональны концентрации дырок p, а двукратно положительно заряженных СТД пропорциональны p². Поскольку легирующие примеси в кремнии являются примесями замещения и диффундируют посредством непрямого вакансионно-междоузельного механизма (см. 2.8, 2.9), их парциальные коэффициенты диффузии пропорциональны концентрациям соответствующих СТД. Суммарный коэффициент диффузии равен сумме парциальных коэффициентов диффузии посредством СТД в различных зарядовых состояниях:

,

поэтому его можно записать в виде

,

где нижний индекс i у парциальных коэффициентов диффузии означает собственный (нелегированный) материал; z – заряд и соответствующая ему степень. Зависимость коэффициента диффузии D от концентрации донор-ной легирующей примеси С_d построена на рис. 5.7. Как видно из рисунка, при малых концентрациях (С < n_i) коэффициент диффузии постоянен и не зависит от концентрации примеси. В этой области слабого легирования концентрация носителей заряда равна собственной n_i, а коэффициент диффу-зии равен собственному

.

В переходной области вблизи С ≈ n_i концентрация носителей заряда связана с концентрацией легирующей примеси известным соотношением

.

При сильном легировании (С > n_i) коэффициент диффузии становится функцией концентрации примеси – сначала линейной (D ~ n ~ C_d), а при С >> n_i – квадратичной (D ~ n² ~ ).

Н а концентрационных профилях примесей фосфора и бора в кремнии при высоких поверхностных концентрациях наблюдаются так называемые перегибы и хвосты в области низких концентраций. Их появление объясняется образованием и диффузией вглубь нейтральных пар примесь–СМА. При концентрациях примеси С ≤ n_k, где n_k – концентрация перегиба, эти пары распадаются с освобождением избыточных СМА. Последние являются причиной ускоренной диффузии примеси в области низких концентраций – на хвосте концентрационного профиля.