5.9. Совместная диффузия легирующих примесей

При совместной диффузии примеси могут влиять друг на друга. Известно, например, что в технологии биполярных ИМС при диффузии эмиттерной легирующей примеси происходит ускоренная диффузия базовой легирующей примеси (так называемый дип- или пуш-эффект [6]). Аналогичный эффект имеет место также при создании ДМОП-транзисторов, подлегировании омических контактов, и его необходимо учитывать при технологическом моделировании ИМС.

Степень ускорения диффузии пропорциональна поверхностной концентрации носителей заряда эмиттерной примеси ( ) при диффузионном легировании или максимальной концентрации носителей заряда ( ) при ионном легировании, т. е. при совместной диффузии коэффициент диффузии базовой примеси выражается следующим образом [18]:

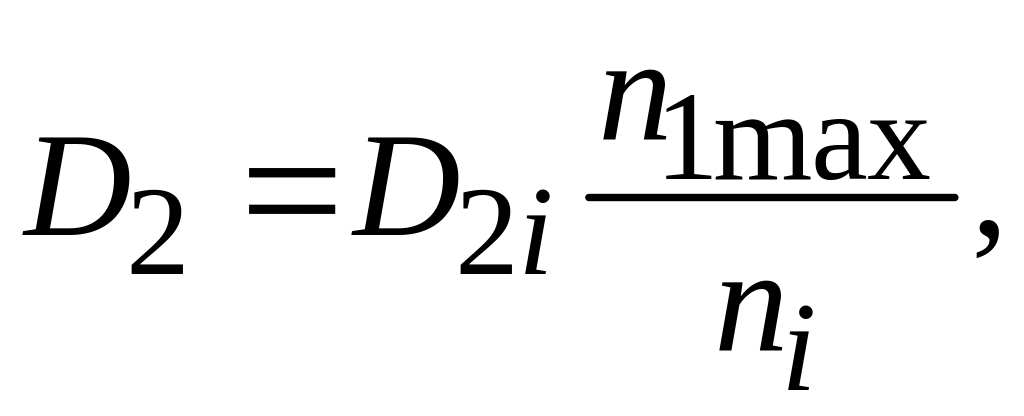
где D_2i – собственный коэффициент диффузии базовой примеси. При моделировании совместной диффузии необходимо рассчитывать перераспределение сразу двух примесей, т. е. решать совместно два уравнения диффузии типа (5.17). В общем случае максимальная концентрация носителей является функцией времени, что необходимо учитывать при моделировании.

5.10. Расчет положения p–n-перехода и слоевого сопротивления

После проведения технологического процесса легирования осуществляется контроль параметров полупроводниковых слоев – глубины залегания p–n-перехода (x_j) и слоевого (поверхностного) сопротивления (R_s). Имея в качестве результата численного моделирования профили распределения легирующих примесей по глубине, можно рассчитать модельные значения этих параметров.

Положение p–n-перехода определяется из условия равенства концентраций донорной (C_d) и акцепторной (C_a) примесей:

Поверхностное (слоевое) сопротивление легированного слоя определяется следующим выражением:

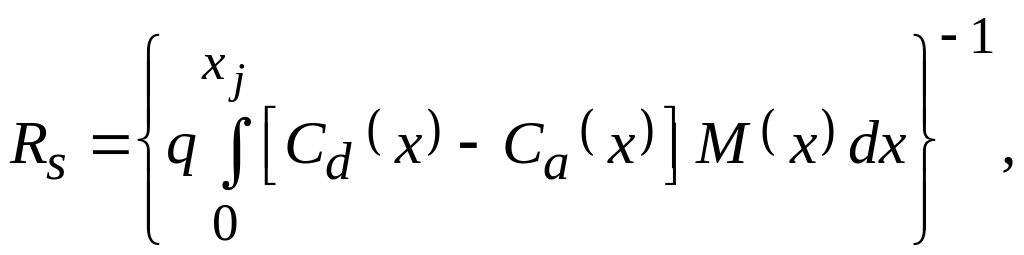(5.19)

где q – заряд электрона (q = 1.6 · 10^–19 Кл); М – подвижность носителей заряда. В качестве C_d и C_a в (5.19) необходимо брать концентрации электрически активных донорной и акцепторной примесей (выражения (5.5)–(5.8)). Зависимость подвижности от координаты M(x) определяется зависимостью подвижности от концентрации основных носителей заряда – электронов n или дырок p, которые в общем случае зависят от глубины. Аппроксимационная формула зависимости подвижности от концентрации носителей заряда n или p имеет вид [19]

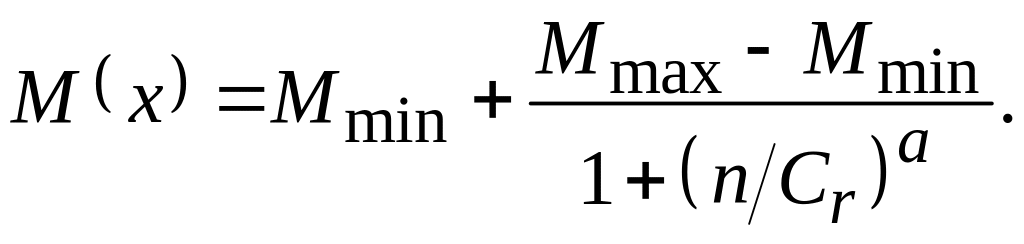
Значения параметров M_min, M_max, C_r и a для донорных и акцепторных примесей в кремнии приведены в прил. 8.

Список литературы

1. Положение об организации курсового проектирования в институте / под ред. В. И. Тимохина; ЛЭТИ. Л., 1979.

2. Методические указания по выполнению учебных документов / под ред. В. И. Тимохина; ЛЭТИ. Л., 1980.

3. Тилл У., Лаксон Дж. Интегральные схемы. М.: Мир, 1985. Гл. 11, 14. С. 292–336, 414–495.

4. Аваев Н. А., Наумов Ю. Е., Фролкин В. Т. Основы микроэлектроники. М.: Радио и связь, 1991. Гл. 7, 8. С. 120–180.

5. Першенков В. С., Севастьянов А. В. Интегральные БиМОП микросхемы // Зарубежная электронная техника. 1989. Вып. 12. С. 49–87.

6. Технология СБИМС / под ред. С. Зи. М.: Мир, 1986. Кн. 2. Гл.10, 11. С. 112–270.

7. Ефимов И. Е., Козырь И. Я., Горбунов Ю. И. Микроэлектроника. М.: Высш. шк., 1986. Гл. 9. С. 286–339.

8. Бубенников А. Н. Моделирование интегральных микротехнологий, приборов и схем. М.: Высш. шк., 1989. Гл. 2. С. 27–74.

9. Таблицы параметров пространственного распределения ионно-им­плантированных примесей / А. Н. Буренков, Ф. Ф. Комаров, М. А. Кумахов, М. М. Темкин; БГУ. Минск, 1980.

10. Александров О. В., Ашкинадзе Н. В., Тумаров Р. З. Комплексообразование при диффузии фосфора в кремний // ФТТ. 1984. Т. 26, вып. 2. С. 632–634.

11. Tsukamoto K., Akasaka Y., Kijima K. Thermal diffusion of ion-implanted As in Si // Japan. J. Appl. Phys. 1980. Vol. 19, № 1. P. 87–95.

12. Бубенников А. Н., Садовников А. Д. Физико-технологическое проектирование биполярных элементов кремниевых БИС. М.: Радио и связь, 1991. Гл. 2. С. 47–108.

13. МОП СБИС. Моделирование элементов и технологических процессов / под ред. П. Антонетти. М.: Радио и связь, 1988. Гл. 7. С. 195–222.

14. Колоссовский А. В. Перераспределение примесей в процессе термического окисления // Обзоры по электронной технике. Сер. 2. 1971. Вып. 6 (288). С. 3–51.

15. Паометс В. Т. Расчет профиля распределения бора при многоэтапной диффузии в окислительных средах // Электронная техника. Сер. 2. 1978. Вып. 3 (121). С. 63–66.

16. Miller R. C., Smits F. M. Diffusion of Sb out of Ge and some properties of Sb–Ge system // Phys. Rev. 1957. Vol. 107, № 1. P. 65–70.

17. Справочник по специальным функциям / под ред. М. Абрамовица, И. Стигана. М.: Наука, 1979.

18. Matsumoto S., Niimi T. Phosphorus diffusion into Si under the condition of controlled surface concentration // Japan. J. Appl. Phys. 1976. Vol.15, № 11. P. 2077–2082.

19. Caughey D. V., Thomas R. E. Carrier mobilities in silicon empirically related to doping and field // Proc. IEEE. 1967. Vol. 55, № 2. P. 2192–2195.

20. Fair R. B., Tsai J. C. C. Theory and direct measurement of B segregation in SiO₂ during dry, near dry and wet O₂ oxidation // J. Electrochem. Soc. 1978. Vol. 125, № 12. P. 2051–2058.

21. Q Сер. ТПО. 1989. № 2. С. 50–55.

22. Fair R. B., Tsai J. C. C. The diffusion of ion implanted As in Si // J. Electrochem. Soc. 1975. Vol. 122, № 12. P. 1689–1696.

23. Ho C. P., Plummer S. E., Dutton R. W. VLSI process modeling-SUPREM 3 // IEEE Trans. El. Dev. 1983. Vol. ED–30, № 11. P. 1438–1453.

24. Ghoshtogore R. N. Low concentration diffusion in Si under sealed tube conditions // Sol. St. Electron. 1972. Vol. 15, № 10. P. 1113–1120.

25. Испарение и сегрегация галлия при нагреве легированного кремния в вакууме /А. В. Кожухов, Б. З. Кантер, С. И. Стенин и др. // Поверхность. 1989. № 3. С. 160–161.

26. Испарение сурьмы из кремния в вакуум / А. В. Кожухов, Б. З. Кантер, Ю. Г. Сидоров, С. И. Стенин // Поверхность. 1990. № 9. С.30–36.

ПРИЛОЖЕНИЯ